-
question_answer1)
A hemispherical bowl is made of steel of \[0.25\text{ }cm\]thickness. The inner radius of the bowl is 5 cm. The volume of steel used is ___. (Use\[\pi =3.141\])
A)
\[42.15\,c{{m}^{3}}\] done
clear
B)
\[41.52\,c{{m}^{3}}\] done
clear
C)
\[41.25\,c{{m}^{3}}\] done
clear
D)
\[40\,c{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer2)
An inverted cone of vertical height 12 cm and the radius of base 9 cm contains water to a depth of 4 cm. Find the area of the interior surface of the cone not in contact with the water. [Use\[\pi =22/7\]]
A)
\[402.12\,c{{m}^{2}}\] done
clear
B)
\[298\,c{{m}^{2}}\] done
clear
C)
\[377.14\,c{{m}^{2}}\] done
clear
D)
\[315\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer3)
A sector of a circle of radius 12 cm has the angle \[{{120}^{\text{o}}}\]. It is rolled up so that two bounding radii are joined together to form a cone. Find the volume of the cone.
A)
\[189.61\text{ }c{{m}^{3}}\] done
clear
B)
\[169.51\text{ }c{{m}^{3}}\] done
clear
C)
\[179.61\text{ }c{{m}^{3}}\] done
clear
D)
\[125.51\text{ }c{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer4)
If the radii of the circular ends of bucket in the form of frustum are 28 cm and 7 cm and the height is 45 cm. The capacity of the bucket is ___.
A)
\[48150\,c{{m}^{3}}\] done
clear
B)
\[48510\,c{{m}^{3}}\] done
clear
C)
\[48105\,c{{m}^{3}}\] done
clear
D)
\[48205\,c{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer5)
The ratio between the volume of two sphere is\[8:27\] what is the ratio between their surface areas?
A)
\[2:3\] done
clear
B)
\[4:5\] done
clear
C)
\[5:6\] done
clear
D)
\[4:7\] done
clear
View Solution play_arrow
-
question_answer6)
A cylinder, whose height is two-thirds of its diameter, has the same volume as a sphere of radius 4 cm. Calculate the radius of the base of the cylinder.
A)
4 cm done
clear
B)
5 cm done
clear
C)
3 cm done
clear
D)
6 cm done
clear
View Solution play_arrow
-
question_answer7)
A right circular cone is \[4.1\text{ }cm\]high and the radius of its base is \[2.1\text{ }cm\]. Another right circular cone is \[4.3\text{ }cm\]high and the radius of the base is\[2.1\text{ }cm\]. Both the cones are melted and recast into a sphere. Find the diameter of the sphere.
A)
\[6.4\,cm\] done
clear
B)
\[4.2\,cm\] done
clear
C)
\[2.1\text{ }cm\] done
clear
D)
\[5.6\text{ }cm\] done
clear
View Solution play_arrow
-
question_answer8)
The number of solid spheres, each of diameter 6 cm that could be moulded to form a solid metal cylinder of height 45 cm and diameter 4 cm, is __.
A)
3 done
clear
B)
4 done
clear
C)
5 done
clear
D)
6 done
clear
View Solution play_arrow
-
question_answer9)
A box opened at the top has its outer dimensions \[10\text{ }cm\text{ }\times 9\text{ }cm\text{ }\times \text{ }2.5\text{ }cm\]and its thickness is \[0.5\text{ }cm,\] find the volume of the metal.
A)
\[92.5\,c{{m}^{3}}\] done
clear
B)
\[72\,c{{m}^{3}}\] done
clear
C)
\[63.5\text{ }c{{m}^{3}}\] done
clear
D)
\[81\text{ }c{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer10)
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be 1/27 of the volume of the given cone, at what height above the base is the section made?
A)
20 cm done
clear
B)
25 cm done
clear
C)
10 cm done
clear
D)
15 cm done
clear
View Solution play_arrow
-
question_answer11)
A cuboidal metal of dimensions \[44\text{ }cm\times 30\text{ }cm\times 15\text{ }cm\]was melted and cast into a cylinder of height 28 cm. Its radius is
A)
20cm done
clear
B)
15cm done
clear
C)
10cm done
clear
D)
25cm done
clear
View Solution play_arrow
-
question_answer12)
Study the question and the statements given below and decide which of the statements) is/are necessary to answer the question. What is the capacity of the cylindrical tank?
| I. The area of the base is 61,600 sq. cm. |
| II. The height of the tank is 1.5 times the radius. |
| III. The circumference of base is 880 cm. |
A)
Only I and II done
clear
B)
Only II and III done
clear
C)
Only I and Ill done
clear
D)
Only II and either I or III done
clear
View Solution play_arrow
-
question_answer13)
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the for of a right circular cone mounted on a hemisphere is immersed into the tub. If the radius of the hemisphere is \[3.5\text{ }cm\]and the height of the cone outside the hemisphere is 5 cm, find the volume of water left in the tub. (Take\[\pi =22/7\])
A)
\[616\,c{{m}^{3}}\] done
clear
B)
\[600\,\,c{{m}^{3}}\] done
clear
C)
\[535\,\,c{{m}^{3}}\] done
clear
D)
\[716\,c{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer14)
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r.
A)
\[\frac{4}{3}\,\pi {{r}^{3}}\,\] done
clear
B)
\[2\,\pi {{r}^{3}}\,\] done
clear
C)
\[\frac{1}{3}\,\pi {{r}^{3}}\,\] done
clear
D)
\[\frac{2}{3}\,\pi {{r}^{3}}\,\] done
clear
View Solution play_arrow
-
question_answer15)
A cylindrical vessel of diameter 4 cm is partly filled with water. 300 lead balls are dropped in it. The rise in water level is\[0.8\,cm.\]. The diameter of each ball is __.
A)
\[0.8\text{ }cm\] done
clear
B)
\[0.4\text{ }cm\] done
clear
C)
\[0.2\text{ }cm\] done
clear
D)
\[0.5\text{ }cm\] done
clear
View Solution play_arrow
-
question_answer16)
A tent is in the shape of a right circular cylinder up to a height of 3 m and then becomes a right circular cone with a maximum height of 13.5 m above the ground. Calculate the cost of painting the inner side of the tent at the rate of \[Rs.\text{ }2\text{ }per\text{ }{{m}^{2}},\]if the radius of the base is 14 m.
A)
Rs.2068 done
clear
B)
Rs.2156 done
clear
C)
Rs.2248 done
clear
D)
Rs.1872 done
clear
View Solution play_arrow
-
question_answer17)
The internal and external diameters of a hollow hemispherical vessel are 24 cm and 25 cm respectively. The cost to paint \[1\text{ }c{{m}^{2}}\]of the surface is\[Rs.\text{ }0.05\].Find the total cost to painting the vessel all over.
A)
Rs.108.32 done
clear
B)
Rs.296.28 done
clear
C)
Rs.101.59 done
clear
D)
Rs. 96.28 done
clear
View Solution play_arrow
-
question_answer18)
A bucket is in the form of a frustum of a cone, its depth is 15 cm and the diameters of the top and the bottom are 56 cm and 42 cm respectively. How many litres can the bucket hold?
A)
\[13\,L\] done
clear
B)
\[27\text{ }L\] done
clear
C)
\[42.94\text{ }L\] done
clear
D)
\[28.49\text{ }L\] done
clear
View Solution play_arrow
-
question_answer19)
To construct a wall 24 m long, \[0.4\text{ }m\]thick and 6 m high, bricks of diamensions \[25\text{ }cm\text{ }\times 16\text{ }cm\text{ }\times \text{ }10\text{ }cm\]each are used. If the mortar occupies 1/10th of the volume of the wall, find the number of bricks used.
A)
12960 done
clear
B)
14420 done
clear
C)
24566 done
clear
D)
14296 done
clear
View Solution play_arrow
-
question_answer20)
In a marriage ceremony of her daughter Poonam, Ashok has to make arrangements for the accommodation of 150 persons. For this purpose, he plans to build a conical tent in such a way that each person have 4 sq. metres of the space on ground and 20 cubic metres of air to breath. What should be the height of the conical tent?
A)
20m done
clear
B)
15m done
clear
C)
12m done
clear
D)
30m done
clear
View Solution play_arrow
-
question_answer21)
A conical vessel of radius 12 cm and height 16 cm is completely filled with water. A sphere is lowered into the water and its sized is such that, when it touches the sides, it is just immersed. What fraction of the water overflows?
A)
\[\frac{3}{8}\] done
clear
B)
\[\frac{4}{7}\] done
clear
C)
\[\frac{1}{2}\] done
clear
D)
\[\frac{5}{9}\] done
clear
View Solution play_arrow
-
question_answer22)
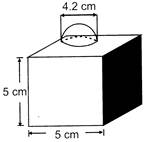
The decorative block shown in the figure is made of two solids, a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter of\[4.2\text{ }cm\]. The total surface area of the block is __.
A)
\[150\,\,c{{m}^{2}}\] done
clear
B)
\[160.86\,c{{m}^{2}}\] done
clear
C)
\[162.86\,c{{m}^{2}}\] done
clear
D)
\[163.86\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer23)
Which of the following statement is INCORRECT?
A)
If from a solid cubic block a hemi-sphere of maximum diameter is cut-off then surface area of the cubic block is decrease. done
clear
B)
If two sphere are melted to form a cylinder then surface area of cylinder is the sum of surface area of two sphere. done
clear
C)
if a wire is wound about a cylinder so as to cover the whole surface, then length of the wire is equal to the surface area of the cylinder. done
clear
D)
All of these. done
clear
View Solution play_arrow
-
question_answer24)
A tent is made in the form of a frustum of a cone surmounted by another cone. The diameter of the base and the top of the frustum are 20 m and 6 m respectively and the height is 24 m. If the height of the tent is 28 m and the radius of the conical part is equal to the radius of the top of the frustum, find the quantity of canvas required.
A)
\[924.71\text{ }{{m}^{2}}\] done
clear
B)
\[1402.23\text{ }{{m}^{2}}\] done
clear
C)
\[1124.56\,{{m}^{2}}\] done
clear
D)
\[1068.57\,{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer25)
The interior of a building is in the form of cylinder of diameter \[4.3\text{ }m\]and height 3.8 m, surmounted by a cone whose vertical angle is a right angle. Find the volume and curved surface area of the building respectively. (Take\[\pi =3.14\]).
A)
\[65.56\text{ }{{m}^{3}},\text{ }71.83\text{ }{{m}^{2}}\] done
clear
B)
\[70.24\text{ }{{m}^{3}},\text{ }62.24\text{ }{{m}^{2}}\] done
clear
C)
\[62.26\text{ }{{m}^{3}},\text{ }75.56\text{ }{{m}^{2}}\] done
clear
D)
\[72.26\text{ }{{m}^{3}},\text{ }66.46\text{ }{{m}^{2}}\] done
clear
View Solution play_arrow
