10th Class Mathematics Pair of Linear Equations in Two Variables Question Bank

done Pair of Linear Equations in Two Variables Total Questions - 25

• question_answer1)
  The sum of two numbers is 8 and the sum 8 of their reciprocals is\[\frac{8}{15}\]. Find the numbers.
  A)
   5, 3                             done clear
  B)
   7, 1     done clear
  C)
          4, 4     done clear
  D)
                      2, 6  done clear
  View Solution play_arrow

• question_answer2)
  The sum of the digits of a two-digit number is 12. The number obtained by interchanging the two digits exceeds the given number by 18. Find the number.               
  A)
   57                   done clear
  B)
   75                   done clear
  C)
   85       done clear
  D)
   58                   done clear
  View Solution play_arrow

• question_answer3)
  The denominator of a rational number is greater than its numerator by 3. If 3 is subtracted from the numerator and 2 is added to the denominator, the new number becomes \[\frac{1}{5}\]. Then the original number was ____.
  A)
   \[\frac{7}{11}\]                      done clear
  B)
   \[\frac{3}{5}\]            done clear
  C)
   \[\frac{5}{8}\]                        done clear
  D)
          \[\frac{4}{7}\]            done clear
  View Solution play_arrow

• question_answer4)
  If am = bl and \[bn\ne cm,\]then the system of equations                              \[ax+by=c\]                \[lx+my=n\]               
  A)
   Has a unique solution.              done clear
  B)
   Has no solution. done clear
  C)
   Has infinitely many solutions.        done clear
  D)
   May or may not have a solution.     done clear
  View Solution play_arrow

• question_answer5)
  The value of k, for which the system of equations \[kx-3y+6=0,\text{ }4x-6y+15=0\]represent parallel lines, is ____.     
  A)
   1                                 done clear
  B)
   2                     done clear
  C)
   3                     done clear
  D)
          4                     done clear
  View Solution play_arrow

• question_answer6)
  If the system of equations \[2x+3y=7\]             \[2ax+(a+b)y=28\] has infinitely many solutions, then the values of a and b respectively are ____.
  A)
   2. 5                 done clear
  B)
   5, 8                 done clear
  C)
   4, 8             done clear
  D)
          3, 6     done clear
  View Solution play_arrow

• question_answer7)
  In a \[\Delta ABC,\] \[\angle C=3\angle B=2(\angle A+\angle B).\]. The three angles will be ____.
  A)
   \[{{20}^{o}}\text{, }{{40}^{o}},\text{ }{{120}^{o}}\]          done clear
  B)
   \[{{30}^{o}},\text{ }{{60}^{o}},\text{ }{{90}^{o}}\] done clear
  C)
   \[{{45}^{o}},\text{ 4}{{\text{5}}^{o}},\text{ }{{90}^{o}}\]              done clear
  D)
   \[{{90}^{o}},\text{ 4}{{\text{0}}^{o}},\text{ 5}{{0}^{o}}\]  done clear
  View Solution play_arrow

• question_answer8)
  \[ax+by+c=0\]does not represent an equation of line when ____.
  A)
   \[a=c=0,\,\,b\ne 0\] done clear
  B)
   \[b=c=0,\,\,a\ne 0\] done clear
  C)
   \[a=b=0~\] done clear
  D)
   \[a=b\ne 0\] done clear
  View Solution play_arrow

• question_answer9)
  The ratio of a 2-digit number to the sum of digits of that number is\[4:1\]. If the digit in the unit place is 3 more than the digit in the tens place, what is the number?
  A)
   63                   done clear
  B)
   36       done clear
  C)
   24                   done clear
  D)
          40       done clear
  View Solution play_arrow

• question_answer10)
  How many values of c, for which the system of equations \[6x+3y=c-3,\text{ }12x+cy=c\] has infinitely many solutions?
  A)
   1                                 done clear
  B)
   2                     done clear
  C)
          3                     done clear
  D)
          Infinite done clear
  View Solution play_arrow

• question_answer11)
  Sum of two numbers is 64 and their difference is 22. Find the numbers.
  A)
   42, 22             done clear
  B)
   43. 21 done clear
  C)
   40, 24         done clear
  D)
          50, 28 done clear
  View Solution play_arrow

• question_answer12)
  if a pair of linear equations in two variables is consistent, then the lines represented by two equations are
  A)
   Always intersecting done clear
  B)
   Parallel done clear
  C)
   Always coincident done clear
  D)
   Intersecting or coincident done clear
  View Solution play_arrow

• question_answer13)
  The solution of the system of equations \[\frac{2x+5y}{xy}=6\] and \[\frac{4x-5y}{xy}+3=0\] (where \[x\ne 0,\,\,y\ne 0\]), is ____.
  A)
   1,2                              done clear
  B)
   0, 0                 done clear
  C)
   \[-1,\text{ }2\]          done clear
  D)
          \[1,-2\] done clear
  View Solution play_arrow

• question_answer14)
  Value of x in pair of linear equations \[36x+24y=702\]and \[24x+36y=558\]is
  A)
   \[\frac{33}{2}\]                                  done clear
  B)
   \[\frac{145}{7}\]        done clear
  C)
   16                   done clear
  D)
          17       done clear
  View Solution play_arrow

• question_answer15)
  Which of the following linear equation coincide with the line\[4x+5y=15\]?
  A)
   \[8x+10y=25\] done clear
  B)
   \[2x+3y=7\] done clear
  C)
   \[7x+14y=17\] done clear
  D)
   \[12x+15y=45\] done clear
  View Solution play_arrow

• question_answer16)
  Arun and Prabhat have some books with them. Once Prabhat said to Arun that, if Arun gives 3 books to Prabhat then Arun will have only - of the books that Prabhat ; will have with him. Then Arun asked frankly that if Prabhat gives him only two books (to Arun), then Prabhat will have as many books as Arun will have. The total number of books that Arun and Prabhat have with them is ____.                     
  A)
   25                             done clear
  B)
   56                    done clear
  C)
             30                     done clear
  D)
           Can't be determined               done clear
  View Solution play_arrow

• question_answer17)
  Places M and N are 90 km apart from each other on a national highway. A truck starts from M and another from N at the same time. If they go in the same direction, then they meet in 9 hours and if they go in opposite directions they meet in - hours. The speed of the trucks are ____.  
  A)
   90 km/hr, 40 km/hr                done clear
  B)
   40 km/hr, 30 km/hr                 done clear
  C)
   20 km/hr, 60 km/hr               done clear
  D)
   50 km/hr, 12 km/hr               done clear
  View Solution play_arrow

• question_answer18)
  A boat goes 32 km upstream and 36 km downstream in 7 hours. In 9 hours, it can go 40 km upstream and 48 km downstream. If x represents the speed of the boat in still water in km/hr and y represents the speed of the stream in km/hr, then____.
  A)
   \[x+y=12,\text{ }x-y=8\] done clear
  B)
   \[x+y=5,\text{ }x-y=11\] done clear
  C)
   \[x+y=6.\text{ x-}y=10\] done clear
  D)
   \[x+y=10,\text{ }x-y=6\] done clear
  View Solution play_arrow

• question_answer19)
  At the end of the year 2002, Ram was half as old as his grandpa. The sum of the years in which they were born is 3854. Age of Ram at the end of year 2003 is ____.
  A)
   50 years          done clear
  B)
   35 years                      done clear
  C)
   51 years        done clear
  D)
          36 years                      done clear
  View Solution play_arrow

• question_answer20)
  On selling a tea-set at 5% loss and lemon- set at 15% gain, a crockery seller gains Rs. 7. If he sells the tea-set at 5% gain and the lemon-set at 10% gain, he gains Rs. 13. Find the actual prices of the tea-set and the lemon-set.
  A)
   Rs.100, Rs.80 done clear
  B)
   Rs. 90, Rs. 100 done clear
  C)
   Rs.120, Rs. 60 done clear
  D)
   Rs.150, Rs. 80 done clear
  View Solution play_arrow

• question_answer21)
  Solve for x and y in the following question. \[\frac{2}{x+2y}+\frac{1}{2x-y}+\frac{5}{9}=0,\] \[\frac{9}{x+2y}+\frac{6}{2x-y}+4=0\]
  A)
   \[x=1,\text{ }y=2\]                done clear
  B)
   \[x=2,\text{ }y=1\]    done clear
  C)
   \[x=2,y=\frac{1}{2}\]    done clear
  D)
          \[x=\frac{1}{2},y=2\] done clear
  View Solution play_arrow

• question_answer22)
  Match the following.

  System of equations	Solutions
  (P) \[2x-3y+15=0\] \[3x-5=0\]	(i) \[x=3,\text{ }y=5\]
  (Q)  \[2x-y=1\] \[4x+3y=27\]	(ii) \[x=1,y=4\]
  (R) \[x+2y-3=0\] \[3x-2y+7=0\]	(iii) \[x=\frac{5}{3},y=\frac{55}{9}\]
  (S) \[4x+\frac{y}{3}=\frac{16}{3}\] \[\frac{x}{2}+\frac{2y}{4}=\frac{5}{2}\]	(iv) \[x=-1,y=2\]

             
  A)
  (P) \[\to \] (iii); (Q) \[\to \] (iv); (R) \[\to \] (i);  (S) \[\to \] (ii)                            done clear
  B)
   (P) \[\to \] (iii); (Q) \[\to \] (i); (R) \[\to \] (iv); (S) \[\to \] (ii) done clear
  C)
   (P) \[\to \] (iii); (Q) \[\to \] (ii); (R) \[\to \] (iv); (S) \[\to \] (i)                             done clear
  D)
   (P) \[\to \] (ii); (Q) \[\to \] (i); (R) \[\to \] (iv); (S) \[\to \] (iii)                           done clear
  View Solution play_arrow

• question_answer23)
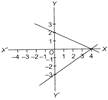
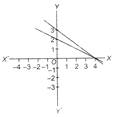
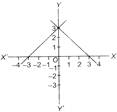
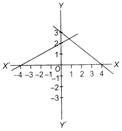
  Which of the following graphs represent the lines \[2x+4y=8\] and\[3x-4y=12\]?
  A)
                                               done clear
  B)
                      done clear
  C)
                                             done clear
  D)
    done clear
  View Solution play_arrow

• question_answer24)
                                      Fill in the blanks.         

  (i) If pair of linear equations is consistent then it has either P or Q solution(s).

  (ii) If the pair of linear equation is inconsistent then it has B solution(s).

  (iii) If the graph of two linear equations coincide then they have S solution(s).

  A)

  P	Q	R	S
  no	Infinite	Unique	Infinite

                  done clear
  B)

  P	Q	R	S
  unique	Infinite	No	Infinite

                  done clear
  C)

  P	Q	R	S
  no	Infinite	Unique	Unique

                  done clear
  D)

  P	Q	R	S
  unique	No	Infinite	No

  done clear
  View Solution play_arrow

• question_answer25)
  Read the statements carefully and state 'T' for true and 'F' for false.           

  (i) The pair of linear equations \[x+2y=5\]and \[7x+3y=13\] has unique solution\[x=2.\text{ }y=1\].

  (ii) \[\sqrt{2}x+\sqrt{3}y=0,\] \[\sqrt{3}x-\sqrt{8}y=0\] has no solution.

  (iii) The values of p and q for which the following system of equations \[2x-y=5,\] \[(p+q)x+(2p-q)y=15\]has infinite number of solutions, is \[p=1\]and\[q=5\].

  A)
   i-T                   ii-F        iii-T done clear
  B)
   i-T                   ii-T       iii-F done clear
  C)
   i-F                   ii-T       iii-T done clear
  D)
   i-F                   ii-F       iii-T done clear
  View Solution play_arrow