Trigonometry

 

Trigonometry

 

The word trigonometry is derived from the Greek word tri (meaning three) gon (meaning sides) and 'metron' meaning measure).

Infact trigonometry is the study of the relations between the sides angles of triangles.

 

TRIGONOMETRY

It is the study of the relations between the sides and angles of triangles.

 

Relation between Radian and Degree Measures

Degree and radian are the unit for measuring an angle, where angle subtended at the centre by an arc of length 1 unit in a circle of radius 1 unit is said to have a measure of 1 radian.

Here, Radian measure \[=\frac{\pi }{180{}^\circ }\times \] Degree measure

Degree measure \[=\frac{180}{\pi }\times \] Radian measure

or, for changing into degree from radian, we multiply by \[\left( \frac{180}{\pi } \right).\]

 

Trigonometric Ratios

The ratios between different sides of a right angled triangle with respect to its acute angles are called trigonometric ratios, Trigonometric ratios for right angled AAJ3C with respect to angle A are given below     

       

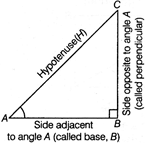
\[\sin A=\frac{BC}{AC}=\frac{P}{H};\]\[\text{cosec}\,A=\frac{AC}{BC}=\frac{H}{P}\]

\[\cos \,A=\frac{AB}{AC}=\frac{B}{H};\]\[\sec \,A=\frac{AC}{AB}=\frac{H}{B}\]

\[\tan \,A=\frac{BC}{AB}=\frac{P}{B};\]\[\cot \,A=\frac{AB}{BC}=\frac{B}{P}\]

Note     To remember trigonometric ratios for sin, cos, tan \[=\frac{LAL}{KKA}\] and for \[\text{cosec,}\]\[sec,\]\[\cot =\frac{KKA}{LAL}\]

 

Relation between Trigonometric Ratios

·   \[\sin \,A=\frac{1}{\cos ec\,A}\]or\[\text{cose}c\,A=\frac{1}{\sin \,A}\]

·   \[\cos \,A=\frac{1}{\sec \,A}\]  or\[\sec \,A=\frac{1}{\cos \,A}\]

·   \[\tan \,A=\frac{\sin A}{\cos A}\]          or\[\tan \,A=\frac{\sin A}{\cos A}\]

 

Trigonometric Ratios of Some Specific Angles

 

Angles Trigonometric Ratios	\[0{}^\circ \]	\[30{}^\circ \]	\[45{}^\circ \]	\[60{}^\circ \]	\[90{}^\circ \]
\[\sin A\]	0	\[\frac{1}{2}\]	\[\frac{1}{\sqrt{2}}\]	\[\frac{\sqrt{3}}{2}\]	1
\[\cos A\]	1	\[\frac{\sqrt{3}}{2}\]	\[\frac{1}{\sqrt{2}}\]	\[\frac{1}{2}\]	0
\[\tan A\]	0	\[\frac{1}{\sqrt{3}}\]	1	\[\sqrt{3}\]	\[\infty \](not defined)
\[\cot A\]	\[\infty \] (not defined)	\[\sqrt{3}\]	1	\[\frac{1}{\sqrt{3}}\]	0
\[\sec A\]	1	\[\frac{2}{\sqrt{3}}\]	\[\sqrt{2}\]	2	\[\infty \](not defined)
\[\text{cosec}\,A\]	\[\infty \](not defined)	2	\[\sqrt{2}\]	\[\frac{2}{\sqrt{3}}\]	1

 

Trigonometric Identities

An equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle involved,

\[\text{cose}{{\text{c}}^{2}}A=1+{{\cot }^{2}}A\]

Rules for Sign of Trigonometric Functions

 

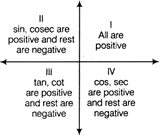
Complementary and Supplementary Angles

Any angle is increased or decreased by \[90{}^\circ \]or\[\frac{\pi }{2},\] then it is called complementary of that angle and if the angle is     increased or decreased by\[180{}^\circ \]then that angle is called   supplementary of that angle. 

                    

Some Complementary Angles

\[\sin \left( \frac{\pi }{2}-\theta  \right)=\cos \theta ;\]\[\sin \left( \frac{\pi }{2}+\theta  \right)=\cos \theta \]

\[\cos \left( \frac{\pi }{2}-\theta  \right)=\sin \theta ;\]\[\cos \left( \frac{\pi }{2}+\theta  \right)=-\sin \theta \]

\[\tan \left( \frac{\pi }{2}-\theta  \right)=\cot \theta ;\]\[\tan \left( \frac{\pi }{2}+\theta  \right)=-\cot \theta \]

\[\cot \left( \frac{\pi }{2}-\theta  \right)=\tan \theta ;\]\[\cot \left( \frac{\pi }{2}+\theta  \right)=-\tan \theta \]

\[\sec \left( \frac{\pi }{2}-\theta  \right)=\sec \theta ;\]\[\sec \left( \frac{\pi }{2}+\theta  \right)=-\cos ec\]

\[\text{cosec}\left( \frac{\pi }{2}-\theta  \right)=\sec \theta ;\]\[\text{cosec}\left( \frac{\pi }{2}\theta  \right)=\sec \theta \]

 

Some Supplementary Angles

\[\sin \,(\pi -\theta )=\sin \theta ;\]\[\sin \,(\pi +\theta )=-sin\theta \]

\[\cos (\pi -\theta )=-\cos \theta ;\]\[\cos \,(\pi +\theta )=-cos\theta \]

\[\tan (\pi -\theta )=-tan\theta ;\]\[\tan \,(\pi +\theta )=tan\theta \]

\[\cot \,(\pi -\theta )=-cot\theta ;\]\[\cot (\pi +\theta )=cot\theta \]

\[\sec \,(\pi -\theta )=-sec\theta ;\]\[\sec \,(\pi +\theta )=-sec\theta \]

\[\text{cosec}\,(\pi -\theta )=cosec\theta ;\]\[\text{cosec}\,(\pi +\theta )=-cosec\theta \]

Also; \[\sin \,(-\theta )=-sin\theta ,\]\[\cos \,(-\theta )=cos\theta \]

Quicker One

 

Important Formulae

Ø  \[\sin (x\pm y)=sin\,x\,cos\,y\pm cos\,xsin\,y\]

Ø  \[\cos (x\pm y)=cos\,x\,cos\,y\mp sin\,x\,sin\,y\]

Ø  \[\tan (x\pm y)=\frac{\tan x\pm \tan y}{1\mp \tan x\tan y}\]

Ø  \[2\sin x\cos y=\sin \,(x+y)+sin\,(x-y)\]

Ø  \[2\sin x\sin y=\cos \,(x-y)-cos\,(x+y)\]

Ø  \[2\cos x\sin y=\sin \,(x+y)-sin\,(x-y)\]

Ø  \[2\cos x\cos y=\cos \,(x+y)+cos\,(x-y)\]

Ø  \[\sin C+\sin D=2\sin \left( \frac{C+D}{2} \right)\cos \left( \frac{C-D}{2} \right)\]

Ø  \[\sin C-\sin D=2\cos \left( \frac{C+D}{2} \right)\sin \left( \frac{C-D}{2} \right)\]

Ø  \[\cos C+\cos D=2\cos \left( \frac{C+D}{2} \right)\cos \left( \frac{C-D}{2} \right)\]

Ø  \[\cos C-\cos D=2\sin \left( \frac{C+D}{2} \right)\sin \left( \frac{D-C}{2} \right)\]

Ø  \[\sin 2x=2\sin x\cos x=\frac{2\tan x}{1+{{\tan }^{2}}x}\]

Ø  \[\cos 2x=\frac{2\tan x}{1-{{\tan }^{2}}x}\]

Ø  \[\sin 3x=3\sin x-4{{\sin }^{3}}x\]

Ø  \[\cos 3x=4co{{s}^{3}}\times -3\cos x\]

Ø  \[\tan 3x=\frac{3\tan x-{{\tan }^{3}}x}{1-3{{\tan }^{3}}x}\]

Ø  \[\tan (x+y+z)\]

\[=\frac{(tan\,x+tan\,y+tan\,z)-tan\,x\,tan\,y\,tan\,z}{1-(tan\,x\times tan\,y+tan\,y\,\tan \,z+\tan z\,\tan x)}\]

 

Maximum and Minimum Value of the

Trigonometrical Functions

 

Function	Minimum value	Maximum value
\[\sin \theta \]	\[-1\]	\[+1\]
\[\cos \theta \]	\[-1\]	\[-1\]
\[a\,\sin \theta \pm b\,\cos \theta \]	\[-\,\sqrt{{{a}^{2}}+{{b}^{2}}}\]	\[+\,\sqrt{{{a}^{2}}+{{b}^{2}}}\]
\[a\,\sin \theta \pm b\,\cos \theta +c\]	\[-\,\sqrt{{{a}^{2}}+{{b}^{2}}}+c\]	\[-\,\sqrt{{{a}^{2}}+{{b}^{2}}}+{{c}^{2}}\]

 

HEIGHT AND DISTANCE

Height and distance is one of the important application of trigonometry used to measured the height of any object or distance from any point.

 

Term Related to Height and Distance

Line of Sight

It is a line drawn from the eye of an observer to the point where the object viewed by the observer.

 

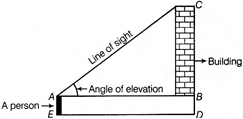
Angle of Elevation

The angle of elevation of the point viewed is the angle formed by the line of sight with the horizontal, when the point being viewed is above the horizontal level.

 

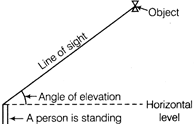
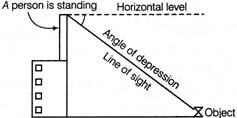
Angle of Depression

When the line of sight is below the horizontal level, then he angle so formed by the line of sight with the horizontal is called the angle of depression.