Set Theory

 

Set Theory

 

SET

A well-defined collection of objects is called a set.

The objects in a set are called its-members or elements.

If a is an element of set A, then we write \[a\in A\](and say a belongs to A) i.e. 'a' is a member of 'A'.

If a does not belong to A, then we write \[a\notin A.\]

By convention, the sets are denoted by capital alphabets

A, B, C,...,X, Y, Z etc. and elements of a set are denoted by a, b, c,..., x, y, z etc.

 

Methods of Representation of Sets

Roster Method

In this method, a set is described by listing all the elements, separated by commas, within braces {}.

e.g. The set of perfect squares upto 100 may be described as:

            \[\{0,1,4,9,16,25,36,49,64,81,100\}\]

Note The order of elements (i.e. position of elements) is not important.

Hence, any element can be written anywhere within braces { }.

 

Set Builder Method

In this method, a set is described by listing its property in the given manner.

The set P(x) is described as

P = {x : P (x) holds} or {x| P(x) holds}

or         \[P=\{x:x\]has the property abc...}

which is read as 'the set of all x such that P(x) holds’. The symbol ‘|’ or ‘:’ is read as ‘such that’.

e.g. The set of perfect squares up to 100 can be written as:

\[P=\{x:x\]is a perfect square and \[0\le x\le 100,\]\[x\in N\}\]

 

TYPES OF SETS

Singleton Set

A set consisting of a single element is called a singleton set.

e.g.   (i) {cat}, {7} etc. (ii) {0} is a singleton set.

 

Empty Set

A set containing no element at all, is called an empty set or a null set or a void set and is denoted by \[\phi .\]

In set builder form, it is expressed as {}.

e.g.          \[\{x:x\in N,9<x<10\}=\phi .\]

Note A set containing at least one element is called a non-empty or on-void set.

 

Finite Set

If a set has finite number of elements that can be counted or listed i.e. the counting of elements surely comes to an end, is called a finite set.

e.g. Set of all the management institutes in the world.

 

Cardinal Number

The number of distinct elements in a finite set is called the 'cardinal number' of the set. E.g. n (A)\[\to \]n is the number of distinct elements in the set A.

 

Infinite Set

If the number of elements of a set is infinite. i.e. which can’t  be counted by natural numbers is called infinite set In other words, if a set is not finite, then it must be an infinite set.

e.g.

(i) Set of all points on the arc of a circle.

(ii) Set of all concentric circles with a given center.

(iii) Number of all lines in a particular plane.

(iv) \[\{x:x\in R,1<x<2\}\]and\[\{x:x\in I,x<10\}\]

 

Equivalent Sets

Two finite sets A and B are equivalent, if their cardinal numbers are same.

i.e.        \[n\,(A)=n\,(B)\]

e.g.       \[A=\{a,e,i,o,u\}\]

and       \[B=\{1,3,5,7,9\}\]

\[\Rightarrow \]   \[n\,(A)=n\,(B)\]

 

Equal Sets

Two sets A and B are said to be equal, if every elements of A is in B and every element of B is in A and is denoted as A = B.

When the elements of A and B are distinct, then \[A\ne B,\]i.e. A and B are not equal.

e.g.       \[A=\{a,e,i,o,u\}\]

and       \[B=\{e,o,i,a,u\}\]

\[\Rightarrow \]   \[A=B\]

 

Subsets

Let A and B be two sets such that every element of A is the element of B (i.e. every element of A is in B), then A is called a subset of B and is denoted as \[A\subseteq B\](read it as ‘A is a subset of B’).

Results on Subsets (i) The empty set \[\phi \]is a subset of every set. (ii) Every set is a subset of itself. (iii) The number of all possible subsets of a set containing n elements is \[{{2}^{n}}.\] (iv)The number of all proper subsets of a set containing n. elements is \[\left( {{2}^{n}}-1 \right).\] (v) The set of all subsets of a given set A is called the power set of A, denoted by P (A). Thus, if A has n elements, P (A) has 2n elements.

 

Superset

If \[A\subseteq B,\]we say that B is a superset of A and we write

\[B\supseteq A\] (read it as ‘B is the superset of A’).

e.g.\[B=\{2,\]\[4,\]\[6,\]\[8,\]\[10\},\]\[A=\{4,8\}\] \[\Rightarrow \]\[B\supseteq A\]

 

Proper Subset

If \[A\subseteq B\]and \[A\ne B,\]then A is called a proper subset of B and denoted as \[A\subset B.\]

e.g.       (i) \[\{5,15,25\}\subset \{15,10,15,20,25\}\]

(ii) \[N\subset W\subset I\subset Q\subset R\]

 

Comparable Sets

Two sets A and B are said to be comparable, if either \[A\subseteq B\]or \[B\subseteq A.\]

 

Universal Set

A set that contains all sets in a given context is called the universal set.

Power Set

The collection or family of all the subsets of a set A is called the power set of A and is denoted by P (A).

e.g. If  \[A=\{1,2,3\},\]then the number of subsets of the P (A) will be \[{{2}^{3}}=8\]

i.e. \[P=(A)=\{\},\]\[\{1\},\]\[\{2\},\]\[\{3\},\]\[\{1,2\},\]\[\{2,3\},\]\[\{1,2,3\}\]

Note: The power set is always non-empty, because the empty set and the given set itself are the members or elements of the power set.

 

VENN DIAGRAMS

In Venn diagrams, the universal set U is represented by points within a rectangle and its subsets are represented by points in closed curves (usually circles) within a rectangle.

 

OPERATIONS ON SETS

Union of Sets

If A and B are two sets, then the union of A and B is the set of all those elements which belong either to A or to B or to both A and B. It is denoted as \[A\cup B\](read as ‘A union B’).

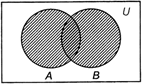
e.g. \[A=\{2,\,3,\,5\},\]\[B=\{1,\,2,\,4,5\}\]\[\Rightarrow \]\[A\cup B=\{1,\,2,\,3,\,4,\,5\}\]

 

Intersection of Sets

If A and B be two sets, then the intersection of A and B is   the set of all those elements that belong to both A and B. It is denoted by \[A\cap B\](read as “A intersection B”).

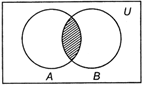
e.g.                   \[A=\{3,6,9,12,15,18\},\]

                        \[B=\{4,6,8,10,12,14,16,18\}\]

\[\therefore \]                  \[A\cap B=\{6,12,18\}\]

 

Disjoint Sets

Two sets A and B are said to be disjoint, if \[A\cap B=\phi .\] If \[A\cap B=\phi ,\]then A and B are said to be intersecting or overlapping sets.

e.g. \[A=\{1,3,5,7,9\},\]\[B=\{2,4,6,8,10\},\]\[C=\{4,\,8,\,12\}\]

Here, \[A\cap B=\phi \]

\[\therefore \] A and B are disjoint sets and \[B\cap C\ne \phi \]

\[\therefore \] B and C are intersecting sets.

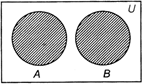
Sets A and B have no elements common.

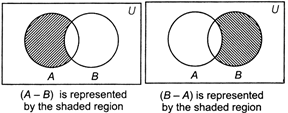
Difference of Sets

The difference of set A and set B (written as \[A-B\]) is the

set of all those elements of A , which do not belong to B.

Thus,    \[A-B=\{x:x\in A\]and\[x\in B\}\]

or         \[A-B=\{x\in A:x\notin B\}\]

Clearly, \[x\in A-B\]\[\Leftrightarrow \]\[x\in A\]and\[x\notin B\]

e.g.       If\[A=\{1,2,3,4,5,6\},\]\[B=\{2,4,6,8,10\}\]

\[\therefore \]      \[A-B=\{1,3,5\}\]and \[B-A=\{8,10\}\]

 

Symmetric Difference of Two Sets

The symmetric difference of sets A and B is the set

\[(A-B)\cup (B-A)\]and is denoted by \[A\Delta B.\]

 

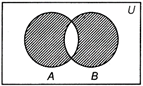
Thus, \[A\Delta B=(A-B)\cup (B-A)=\{x:x\notin A\cap B\}\]

 

Complement of a Set

If U is the universal set and a set A is such that \[A\subset U,\]then the complement of A with respect to U is denoted by A' or \[{{A}^{\subset }}\] or U – A and is defined by the set of all those elements of U which are not in A.

Thus,    \[A'=\{x\in U:x\notin A\}\]

Clearly, \[x\in A'\]\[\Leftrightarrow \]\[x\in A\]

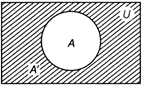
A' is shown by the shaded region

e.g.       \[U=\{2,3,5,7,11,13,...\}\]

\[A=\{2\}\]

\[A'U-A=\{3,5,7,11,13,...\}\]

 

ALGEBRAIC LAWS OF SETS

1.            Idempotent Laws For any set A, we have

(i) \[A\cup A=A\]

(ii) \[A\cap A=A\]

2.            Identity Laws For any set A, we have

(i) \[A\cup \phi =A\]

(ii) \[A\cap B=B\cap A\]

3.            Commutative Laws For any two sets A and B, we have

(i) \[A\cup B=B\cup A\]

(ii) \[A\cap B=B\cap A\]

4.            Associative Laws If A, B and C are any three sets, then.

(i) \[(A\cup B)\cup C=A\cup (B\cup C)\]

(ii) \[A\cap (B\cap C)=(A\cap B)\cap C\]

5.            Distributive Laws If A, 5 and C are any three sets, then

(i) \[A\cup (B\cap C)=(A\cup B)\cap (A\cup C)\]

(ii) \[A\cap (B\cup C)=(A\cap B)\cup (A\cap C)\]

6.            De-Morgan's Laws If A and B are any two sets, then

(i)\[(A\cup B)'=A'\cap B'\]

(ii) \[(A\cap B)'=A'\cup B'\]

 

Some Important Results on Operations on Numbers

(i) \[A-B=A\cap B'\]

(ii) \[B-A=B\cap A'\]

(iii) \[A-B=A\]\[\Leftrightarrow \]\[A\cap B=\phi \]

(iv) \[(A-B)\cup B=A\cup B\]

(v) \[(A-B)\cap B=\phi \]

(vi) \[A\subseteq B\]\[\Leftrightarrow \]\[B'\subseteq A'\]

(vii) \[(A-B)\cup (B-A)=(A\cup B)-(A\cap B)\]

 

Some Important Results on Numbers of Elements in Sets

If A, B and C are finite sets and U is the finite universal set, then

(i) \[n\,(A\cup B)=n\,(A)+n\,(B)-n\,(A\cap B)\]

(ii)\[n\,(A\cup B)=n\,(A)+n\,(B)-n\,(A\cap B)\]\[\Leftrightarrow \]A, B are disjoint non-void sets.

(iii) \[n\,(A-B)=n\,(A)-n\,(A\cap B)\]

i.e. \[n\,(A-B)+n\,(A\cap B)=n\,(A)\]

(iv)\[n\,\,(A\,\Delta \,B)=\]Number of elements which belong to exactly one of A or B.

\[=n\,(A)+n\,(B)-2n\,(A\cap B)\]

(v) \[n\,(A\cup B\cup C)=n\,(A)+n\,(B)+n\,(C)\]

\[-\,n\,(A\cap B)-n\,(B\cap C)-n\,(A\cap C)+n\,(A\cap B\cap C)\]

(vi) Number of elements in exactly two of the sets

\[A,B,C=n\,(A\cap B)+n\,(B\cap C)+n\,(C\cap A)-\,3n\,(A\cap B\cap C)\]

(vii) Number of elements in exactly one of the sets

\[A,B,C,=n\,(A)+n\,(B)+n\,(C)-2n\,(A\cap B)-\,2n\,(B\cap C)\]

\[-\,2n\,(A\cap C)+3n\,(A\cap B\cap C)\]

(viii) \[n\,(A'\cup B)=n\,[(A\cap B)']=n\,(U)-n\,(A\cap B)\]

(ix) \[n\,(A'\cap B')=n\,[(A\cup B)']=n\,(U)-n\,(A\cup B)\]