LCM and HCF

 

LCM and HCF

 

HCF and LCM (Highest Common Factor and Least Common Multiple) is one of the important operation on number system. To understand HCF and LCM we have to know the meaning, factors and multiples.

 

FACTORS AND MULTIPLES

If a number divides another number exactly

(without leaving any remainder), then the number which divides is called a factor of the number and the number that has been divided is known as the multiple of the number which divides it.

e.g.,      \[\frac{16}{8}=2\] (no remainder)

 

LCM (LEAST COMMON MULTIPLE)

The LCM of two or more given numbers is the least number to be exactly divisible by each of them.

e.g.. We can obtain LCM of 4 and 12 as follows

Multiple of \[4=4,\]\[8,\]\[12,\]\[16,\]\[20,\]\[24,\]\[28,\]\[32,\]\[36,...\]

Multiple of \[12=12,\]\[24,\]\[36,\]\[48,\]\[60,\]\[72,...\]

Common multiple of 4 and \[12=12,\]\[24,\]\[36,...\]

\[\therefore \]      LCM of 4 and \[12=12\]

 

Methods of Calculation of LCM

Prime Factorization Method

Following are the steps to obtain LCM through prime factorization method

Step I   Resolve the given numbers into their prime factors.

Step II Find the product of the highest powers of all the factors that occur in the given numbers.

Step III This product of terms of highest powers of all

factors is the required LCM.

e.g., Find the LCM of 8, 12 and 15.

Sol.                             

           

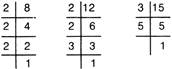
Factors of 8=2x2x2= 23

Factors of 12=2x2x3= 22 x 31

Factors of 15 = 3 x 5 = 31 x 51

Here, the prime factors that occur in the given numbers are 2, 3 and 5 and their highest power are \[{{2}^{3}},\,{{3}^{1}}\] and \[{{5}^{1}}.\]

\[\therefore \] Required LCM \[={{2}^{3}}\times {{3}^{1}}\times {{5}^{1}}=8\times 3\times 5=120\]

 

Division Method

Following are the steps to obtain LCM through division method

Step I   Write down the given numbers in a line, separating them by commas.

Step II Divide by anyone of the prime numbers which exactly divides atleast any two of the given numbers.

Step III Set down the quotients and the divided numbers

in a line below the 1st.

Step IV Repeat the process until you get a line of numbers

which are prime to one another.

Step V  The product of all divisors and the numbers in the last Ira? will be the required LCM.

e.g.. What will be the LCM of 15, 24, 32 and 45?

Sol.     

\[\therefore \] Required LCM

\[=2\times 2\times 2\times 3\times 5\times 4\times 3=1440\]

Lowest Common Multiple of Polynomials

Let p(x) and q(x) are two polynomials, then LCM of p(x) and \[q\,\,(x)=\frac{p\,\,(x)\times q\,\,(x)}{\text{HCF}\,\,\text{of}\,\,p(x)\,\,\text{and}\,\,q\,\,(x)}\]

e.g. Find the LCM of \[(x+3){{(x-2)}^{2}}\] and \[(x-2)(x-6).\]

Sol.      Here, \[p(x)=(x+3){{(x-2)}^{2}}\] and

\[q(x)=(x-2)(x-6)\]

            We know that, LCM of \[p(x)\]and \[q(x)\]

                        \[=\frac{p\,\,(x)\times q\,\,(x)}{\text{HCF}\,\,\text{of}\,\,p\,\,(x)\,\,\text{and}\,\,q\,\,(x)}\]

HCF of\[p\,\,(x)\]and \[q\,\,(x)=(x-2)\]

Product of\[p\,\,(x)\] and \[q\,\,(x)=(x+3){{(x-2)}^{3}}(x-6)\]

\[\therefore \]      \[\text{LCM}=\frac{(x+3){{(x-2)}^{3}}(x-6)}{(x-2)}\]

            \[=(x+3){{(x-2)}^{2}}(x-6)\]

 

HCF (HIGHEST COMMON FACTOR)

HCF of two or more numbers is the greatest number which divides each of them exactly.

e.g., 6 is the HCF of 12 and 18 as there is no number greater then 6 that divides both 12 and 18.

Similarly, 3 is the highest common factor of 6 and 9.

HCF is also known as 'Highest Common Divisor' (HCD) and ‘Greatest Common Multiple’ (GCM).

 

Methods of Calculation of HCF

Prime factorization Method

Below are the given steps for calculating HCF through prime factorization method

Step I   Break the given numbers into prime factors.

Step II Find the product of all the prime factors common to all the numbers.

Step III The product of common prime factors with the least powers gives HCF.

e.g., Find the HCF of 24, 30 and 42.

Sol.     

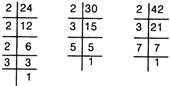
\[\therefore \]      Factors of \[24=2\times 2\times 2\times 3=({{2}^{3}}\times {{3}^{1}})\]

            Factors of \[30=2\times 3\times 5=({{2}^{1}}\times {{3}^{1}}\times {{5}^{1}})\]

            Factors of \[42=2\times 3\times 7=({{2}^{1}}\times {{3}^{1}}\times {{7}^{1}})\]

\[\therefore \] The product of common prime factors with the least powers

 

Division Method

Following are the steps to obtain HCF through division method

Step I   Divide the larger number by the smaller one.

Step II Divide the divisor by the remainder.

Step III Repeat Step II till the remainder becomes zero.

The last divisor is the required HCF.

e.g.,      Find the HCF of 26 and 455.

Sol.     

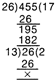
\[\therefore \] Required HCF = 13

 

Highest Common Factor/Greatest

Common Divisor of Polynomials

Let p(x) and q(x) are two polynomials then, HCF of p(x) and q(x) = Common Divisor of p(x) and q(x).

If \[p\,\,(x)=(1+{{x}^{3}})\] and \[q\,\,(x)=(1-x+{{x}^{2}})(1+x+{{x}^{2}})\]

Factor of \[(1+{{x}^{3}})=(1+x)(1-x+{{x}^{2}})\]

and       \[(1-x+{{x}^{2}})(1+x+{{x}^{2}})=(1-x+{{x}^{2}})\times (1+x+{{x}^{2}})\]

Here, Common Divisor in maximum indices \[=(1-x+{{x}^{2}})\]

So, HCF of \[p\,\,(x)\] and \[q\,\,(x)=\] Common Divisor in maximum indices \[=(1-x+{{x}^{2}})\]

 

LCM and HCF of Fractions

The LCM and HCF can be obtained from the following formula

LCM of fractions \[\text{=}\frac{\text{LCM}\,\,\text{of}\,\,\text{numerators}}{\text{HCF}\,\,\text{of}\,\,\text{denominators}}\]

HCF of fractions \[\text{=}\frac{\text{HCF}\,\,\text{of}\,\,\text{numerators}}{\text{LCM}\,\,\text{of}\,\,\text{denominators}}\]

 

LCM and HCF of Decimals

Below are given the steps to calculate LCM and HCF of decimals

Step I   If necessary, make the same number of decimal places in all the given numbers.

Step II Find their LCM/HCF as if they were integers

Step III Mark in the result as many decimal places there are in each of the numbers.

 

Questions based on Bells/Circular Track

To solve such questions, following steps are used

Step I   Find the LCM of given time intervals.

Step II Obtained LCM is added to the initial time (if time is given) and result of this addition will be our answer (the next time when bells ring or the person meets together).

 

Quicker One

Ø   These formulae are true for any number of numbers

Ø   Product of two numbers

= HCF of the numbers \[\times \]LCM of the numbers

Ø   The greatest number which divides the numbers x, y and z, leaving remainders a, b and c, respectively.

\[=HCF\,\,\text{of}\,\,(x-a),\]\[(y-b),\]\[(z-c)\]

Ø   The least number which when divided by x, y and z leaves the remainders a, b and c  respectively, is given by\[[LCM\,\,of\,\,(x,\,y,\,z)]-k.\]

Where, \[k=(x-a)=(y-b)=(z-c)\]

Ø   The least number which when divided by x, y and z leaves the same remainder k in each case, is given by \[[LCM\,\,of\,\,(x,\,y,\,z)+k]\]

Ø   The greatest number that will divide x, y and z leaving the same remainder in each case, is given by \[[HCF\,\,\text{of}\,\,|x-y|,|y-z|,|z-x|]\]

Ø   When the HCF of each pair of n given numbers is a and their LCM is b, then the product of these numbers is given by \[{{(a)}^{n-1}}\times b\] or \[{{(HCF)}^{N-1}}\times LCM\]