Coordinate Geometry and Graphs of Linear Equations

 

Coordinate Geometry and Graphs of Linear Equation

 

THE CARTESIAN PLANE

The exact position on the two-dimensional plane is an ordered pair of numbers in the form (x, y). In it, there are two fixed line drawn, which are perpendicular to each other and are known as axes. The horizontal line known as X-axis while the vertical one is termed as Y-axis and the intersection point of these axes are known as origin (0).

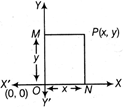
Here, x is called the abscissa of point P and y is called the ordinate of point P. Thus, for a given point, the abscissa and ordinate are distances of the point from Y and X-axes, respectively.

QUADRANTS

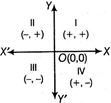
The axes X'OX and Y'OY divide the whole plane into four parts which are called quadrants. Here, OX and OX' are called the positive and negative directions respectively of X-axis and similarly OY and OY' are the positive and negative directions, respectively of y-axis.

In 1st quadrant, x > 0, y > 0

In 2nd quadrant, x < 0, y > 0

In 3rd quadrant, x < 0, y < 0

In 4th quadrant, x > 0, y < 0

The coordinates of any point on the X-axis are of the form (x, 0) and on the Y-axis are of the form (0, y). If the a-coordinate or abscissa of a point is zero, then it would be somewhere on the Y-axis and if its

Y-coordinate or ordinate is zero, then it would be on X-axis.

 

DISTANCE FORMULAE

The distance between any two points is the length of the line segment joining them.

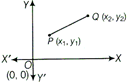
i. e.,\[D=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]

or \[D=\sqrt{{{(Difference\,of\,abscissa)}^{2}}+{{(Differene\,of\,ordinates)}^{2}}}\]

If 0 is the origin and P \[({{x}_{1}},{{y}_{1}})\] is any point, then from the distance formula, we have   

 \[OP=\sqrt{{{({{x}_{1}}-0)}^{2}}+{{({{y}_{1}}-0)}^{2}}}=\sqrt{{{x}_{1}}+{{y}_{1}}^{2}}\]

If the line PQ is parallel to Y-axis, then \[PQ=\left| {{y}_{2}}-{{y}_{1}} \right|\]

If the line PQ is parallel to X-axis, then \[PQ=\left| {{x}_{2}}-{{x}_{1}} \right|\]

 

IMPORTANT RULES

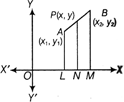
Let 0 be the origin and OX, OY are the X and Y-axes, respectively. Let A \[({{x}_{1}},{{y}_{1}})\]and B \[({{x}_{2}},{{y}_{2}})\] be any two given points and P (x, y) be the point which divides the line segment joining the points A \[({{x}_{1}},{{y}_{1}})\]and B \[({{x}_{2}},{{y}_{2}})\]in the ratio of m: n .

Case I For external division,

\[x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},y=\frac{m{{y}_{2}}-n{{y}_{1}}}{m-n}\]

Case II For internal division,

\[x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\]

The coordinates of the points of trisection P and Q of the line segment joining A \[({{x}_{1}},{{y}_{1}})\]and B \[({{x}_{2}},{{y}_{2}})\]are

\[\left( \frac{2{{x}_{1}}+{{x}_{2}}}{3},\frac{2{{y}_{1}}+{{y}_{2}}}{3} \right)\]

and                   \[\left( \frac{{{x}_{1}}+2{{x}_{2}}}{3},\frac{{{y}_{1}}+2{{y}_{2}}}{3} \right),\] respectively.

The mid-point line joining P \[({{x}_{1}},{{y}_{1}})\]and Q\[({{x}_{2}},{{y}_{2}})\] is

\[\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right),\]Straight line ax + by + c = 0 divides the join of points P \[({{x}_{1}},{{y}_{1}})\]

and Q \[({{x}_{2}},{{y}_{2}})\]in the ratio \[\frac{a{{x}_{1}}+b{{y}_{1}}+{{c}_{1}}}{a{{x}_{2}}+b{{y}_{2}}+{{c}_{2}}}.\]

 

Note: If this ratio is negative, then the line divides externally and if the ratio is positive, then the line divides internally.

 

Area of a Triangle

Let A\[({{x}_{1}},{{y}_{1}})\], B \[({{x}_{2}},{{y}_{2}})\]and C\[({{x}_{3}},{{y}_{3}})\]be the coordinates of the vertices of \[\Delta ABC.\]

\[\therefore \]Area of \[\Delta ABC=\frac{1}{2}[{{x}_{1}}({{y}_{2}}-{{y}_{3}})+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}})]\]

\[=\frac{1}{2}\left| \begin{matrix}

   {{x}_{1}} & {{y}_{1}} & 1  \\

   {{x}_{2}} & {{y}_{2}} & 1  \\

   {{x}_{3}} & {{y}_{3}} & 1  \\

\end{matrix} \right|\]

 

Straight Line

A curve is said to be a straight line, if for any two points are taken on the curve, every point on the line segment joining the two points lies on the curve.

 

Slope or Gradient of a Line

If a line AB makes an angle 9 with the positive X-axis, then m or \[\tan \,\theta \]is called the slope or gradient of the line.

i.e.,                   \[m=\tan \,\theta \]

·         If \[0{}^\circ <\theta <90{}^\circ ,\]then \[\theta \] is an acute angle; the slope is positive.

·         If \[\theta =0{}^\circ ,\]then either the line is X-axis or it is parallel to X-axis; the slope is 0.

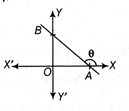
If \[0{}^\circ <\theta <90{}^\circ ,\]then \[\theta \] is an obtuse angle; the slope is negative.

If \[\theta =0{}^\circ ,\]then either the line is X-axis or it is parallel to X-axis; the slope is not defined.

 

Slope of a Line Passing through Two Points

If a line l passes through A \[({{x}_{1}},{{y}_{1}})\] and B\[({{x}_{2}},{{y}_{2}})\], then the slope of line l is given by \[m=\tan \,\theta =\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]

If a line is parallel to -if-axis, then slope of the line is zero.

If a line is perpendicular to Y-axis, then slope of a line is not defined. If the equation of line is ax + by + c = 0, then

\[\text{Slope}\,\text{of}\,\text{line=}\frac{-\,\text{(Coefficient}\,\text{of}\,\text{x)}}{\text{(Coefficient}\,\text{of}\,\text{y)}}\,=-\frac{a}{b}\]

 

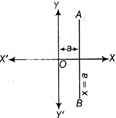
Equation of a Line Parallel to X-axis

Let AB be a straight line parallel to X-axis at a distance 'b' units from it. Thus, if P (x, y) is any point on AB, then y = b. Hence, the equation of a line parallel to X-axis at a distance b is y = b. If a line is parallel to x-axis at a distance b and is below the X-axis, then its equation is \[y=-\,b.\] Equation of X-axis is \[y=0.\]

 

Equation of a Line Parallel to Y-axis

Let AB be a line parallel to Y-axis and at a distance a from

 

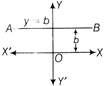
it. Then, the abscissa of every point on AB is a. So, it can

be treated as the locus of a point at a distance a from Y axis, i.e., x = a. Again, if a line parallel to Y-axis, at a distance a and to the left of r-axis,

then its equation is \[x=-\,a.\]

Equation of Y-axis is x = 0.

 

Equation of a Straight Line in Different Forms

General Form

General linear equation in x and y, say ax + by + c = 0, represents an equation of line.

 

Cartesian Form                 

An equation of the form y = f(x) or \[\phi \](x, y) = 0, where x and y are the cartesian coordinates of the moving point is said to be cartesian equation of a straight line.

 

Slope-Intercept Form

The equation of a line with slope m and making an intercept con y-sais is \[y=mx+c.\]

 

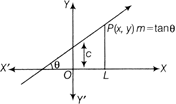
Parametric Form

Equation of the line passing through\[({{x}_{1}},{{y}_{1}})\]and making an angle\[\theta \]with the positive direction of X-axis in anti-clockwise rotation is given by \[x={{x}_{1}}+r\,\cos \,\,\theta \]and \[y={{y}_{1}}+r\sin \,\theta \]where, r is known as parameter.

 

Point-Slope Form             

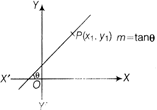
The equation of a line which passes through the point \[p\,({{x}_{1}},{{y}_{1}})\]and has the slope m, is \[y-{{y}_{1}}=m\,(x-{{x}_{1}})\]

 

Two Points Form

The equation of a line passing through two points A \[({{x}_{1}},{{y}_{1}},)\]and B \[({{x}_{2}},{{y}_{2}})\] is given by

\[\frac{y-{{y}_{1}}}{{{y}_{2}}-{{y}_{1}}}=\frac{x-{{x}_{1}}}{x{{\,}_{2}}-{{x}_{2}}}\]

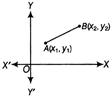
If a line AB passes through two points A \[({{x}_{1}},{{y}_{1}})\]and B \[({{x}_{2}},{{y}_{2}})\], then the equation of line is

\[\left| \begin{matrix}

   x & y & 1  \\

   {{x}_{1}} & {{y}_{1}} & 1  \\

   {{x}_{2}} & {{y}_{2}} & 1  \\

\end{matrix} \right|=0\]

 

Intercept Form

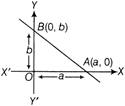
If a line makes intercepts a and b on X and Y-axes respectively, then the equation of line is

\[\frac{x}{a}+\frac{y}{b}=1\]

 

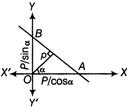
Perpendicular Form                       

Equation of a line, if perpendicular distance of origin from the line is p and perpendicular drawn from the origin to the line is making an angle a with the positive direction of x-axis, then equation of line is \[x\,\cos \,a+y\,\sin \,a=p\]

Equation of a Line Parallel to a Given Line

Let ax + by + c = 0 be any given straight line. Then, equation of a line parallel to the line ax + by + c = 0 is             ax + by + K = 0, where K is an arbitrary constant.

\[\Rightarrow \] Slope of line (i) = Slope of line (ii)         

i.e., \[{{m}_{1}}={{m}_{2}}\]                     

Parallel lines differ by a constant.                  

  

Equation of a Line Perpendicular to a Given Line                    

Let ax + by + c = 0 be any given straight line. Then, equation of a straight line perpendicular to the given line is      

\[bx-ay+K=0\] Where, K is an arbitrary constant.

Slope of line (i) \[\times \] Slope of line (ii) \[=-1\]\[\Rightarrow \]\[{{m}_{1}}{{m}_{2}}=-1\]