Train and Boat

 

Train and Boat

 

Problems on trains/boats are based on the basic concept of speed, time and distance except a difference that length of train is also considered, in case of train whereas the length of boat is meaningless for consideration.

 

TRAIN

A train is said to have crossed an object (stationary or moving) only when the last coach (end) of the train crosses object completely.

 

Relative Speed

(i) If two bodies are moving in the same direction at a km/h and b km/h, where \[(a>b),\] then their relative speed is given by \[(a-b)\,km/h.\]

(ii) If two bodies are moving in opposite direction at a km/h and b km/h, then their relative speed is given by \[(a+b)\,km/h.\]

Case I  When a train crosses a man/pole/tree (in stationary form)

Let a train having speed is S and length L, crosses a pole in T time, then\[S=\frac{L}{T}.\](here, the breadth of man, tree, pole is negligible with respect to the train.

 

Case II When a train crosses a platform.

Let a train having speed of S and length \[{{L}_{1}},\] crosses a platform whose length is \[{{L}_{2}}\] in time T.

Then, \[S=\frac{{{L}_{1}}+{{L}_{2}}}{T}\]

 

Case III When a train crosses another running train. Let

a train having speed \[{{S}_{1}}\] and length \[{{L}_{1}}\] crosses another train which is travelling in opposite direction at a speed at \[{{S}_{2}}\] and length \[{{L}_{2}}\] in T time. Then, \[{{S}_{1}}+{{S}_{2}}=\frac{{{L}_{1}}+{{L}_{2}}}{T}\] (both object having length and speed)

 

Note:

(i) If both object having length (\[{{L}_{1}}\] and \[{{L}_{2}}\]), then the length is always sum (i.e., \[{{L}_{1}}+{{L}_{2}}\]).

(ii) If both object having speed \[{{S}_{1}}\] and \[{{S}_{2}},\] then the speed are added (when direction is opposite) and subtracted (when direction is same).

 

Case IV When a moving train crosses a man who is

            running.

Let a train having speed \[{{S}_{1}}\] and length \[{{L}_{1}}\] crosses a man, who is running at a speed of \[{{S}_{2}}\]in the same direction in T time. Then, \[({{S}_{1}}-{{S}_{2}})=\frac{{{L}_{1}}}{T}.\] (since, man has negligible breadth)

 

Case V When a moving train crosses a man who is sitting

            into a moving train.

Let a train having speed \[{{S}_{1}}\]and length \[{{L}_{1}}\] crosses a man who is sitting in another train which is travelling in opposite direction at speed of \[{{S}_{2}}\] and length \[{{L}_{2}}\] in time to, then \[{{S}_{1}}+{{S}_{2}}=\frac{{{L}_{1}}}{T}.\]

BOAT AND STREAM

Upstream

When an object is moving against (opposite) direction in which the water in the stream is flowing, then the object is said to be moving upstream.

 

Downstream

When an object is moving in the direction in which the water in the stream is flowing, then the object is said to be moving downstream.

 

Some Terms Related to Boats and Streams Still Water

When an object is moving in water where there is no mew water, the object can move in any direction with a uniform speed, then the object is said to be moving in still water-

 

Case I  Speed of the boat/boatman in still water, denoted by x km/h.

           

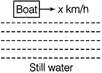
Case II Speed of the water, denoted by y km/h.

                       

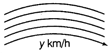
Case III Speed of the boatman or boat in along the

Stream (water) is called downstream speed of boatman or boat, denoted by u km/h.

           

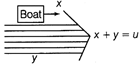
Case IV Speed of the boatman or boat against the stream

is called upstream, speed by boatman, denoted by u km/h.

Conclusion There are four speed.

           

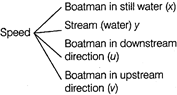
Hence,

Downstream speed

\[u=x+y\]         ... (i)

Upstream speed \[v=x-y\]            ... (ii)

When, x is original speed of boat in still water, y

is speed of water or stream.

From Eqs. (i) and (ii), we get

Speed of boatman \[x=\frac{u+v}{2},\]

Speed of water or stream \[y=\frac{u-v}{2}\]

Quicker One

Ø  Time taken by a train of length \[{{l}_{1}}\] m moving at a speed of s km/h to cross a platform /tunnel /bridge of length \[{{l}_{2}}m\] is \[\frac{{{l}_{1}}+{{l}_{2}}}{s}\times \left( \frac{18}{5} \right)\text{s}\]

Ø  Time taken by a train of length / m moving at a speed of \[{{s}_{1}}\] km/h to cross a car / bus / man moving at a speed of \[{{s}_{2}}\] km/h in same / opposite direction is \[\frac{l}{{{s}_{1}}\pm {{s}_{2}}}\times \left( \frac{18}{5} \right)s\]

Note \[+\]For opposite direction, \[-\]For same direction

Ø  time taken by a train of length \[{{l}_{1}}\] m moving at a speed of \[{{s}_{1}}\]km/h to cross another train of length \[{{l}_{2}}\]moving at a speed of \[{{s}_{2}}\]km/h in same/opposite direction is \[\frac{{{l}_{1}}+{{l}_{2}}}{s{{}_{1}}\pm {{s}_{2}}}\times \left( \frac{18}{5} \right)s\]

Note \[+\]For opposite direction; \[-\]For same direction

Ø  If train crosses two persons moving at speeds of \[{{s}_{1}}\]km/h and \[{{s}_{2}}km/h\] in time \[{{t}_{1}}\] and \[{{t}_{2}}\] h respectively, then length of train is given by \[=\frac{{{s}_{1}}-{{s}_{2}}}{{{T}_{1}}-{{T}_{2}}}\times \left( {{T}_{1}}\times {{T}_{2}} \right)\] [Difference is taken as positive difference]

It two trains start at the same time from points A and b towards each other and after crossing each other, they take\[{{t}_{1}}\] and time in reaching points B and A respectively, then ratio of their speed\[=\sqrt{\frac{{{t}_{2}}}{{{t}_{1}}}}\]or \[\frac{{{s}_{1}}}{{{s}_{2}}}=\frac{\sqrt{{{t}_{2}}}}{\sqrt{{{t}_{1}}}}\]

Ø  If speed of boat in still water is x km/h and speed of stream is y km/h and to go and come back from a point the time taken is \[{{z}_{1}}\]then the distance between both points \[=\frac{z({{x}^{2}}-{{y}^{2}})}{2x}km\]

Ø  If speed of boat in still water is x km/h and speed of stream is y km/h, then to go and come back a distance of d km between two fixed points, the total time take \[=\frac{d}{x+y}+\frac{d}{x-y}h\]

Ø  A person can row a certain distance downstream in x h and returns upstream the same distance in y h. When the stream flows at the rate of a km/h, then the speed of the man \[=\frac{a\,(x+y)}{y-x}km/h\]

Ø  If in case of trick 3, man's speed in still water is b km/h and we are asked to find the speed of stream, then trick 3 takes the form as

Speed of the stream \[=\frac{b(y-x)}{x+y}\]