Work, Power, Energy
Category : Railways
Work, Power, Energy
Work
Work done by the force is measured by the product of magnitude of force and the displacement of the point of application in the direction of force.
i.e., W=F.S
Work done = component of force in the direction of the displacement \[\times \] magnitude of displacement.
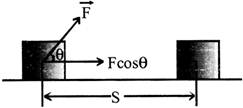
i.e., W= (F cos q) S=F S cos q or W=\[\overrightarrow{F.}\,\overrightarrow{S}\]
In terms of rectangular components, work done
W=\[\overrightarrow{F.}\,\overrightarrow{d}\]
\[W=(\hat{i}\,{{F}_{x}}+\hat{j}\,{{F}_{y}}+\hat{k}\,{{F}_{Z}}).(\hat{i}\,\,dx+\hat{j}\,dy+\hat{k}\,\,dz)\]
\[={{F}_{x}}dx+{{F}_{y}}dy+{{F}_{Z}}dz\]
Units of work
SI unit: joule (J). One joule of work is said to be done when a force of one newton displaces a body by one metre in the direction of force
\[1\,\,joule={{10}^{7}}erg\]
Dimensions of work:
Work = force, displacement
\[=[ML{{T}^{-2}}][L]=[M{{L}^{2}}{{T}^{-2}}]\]
Work Done in Pulling and Pushing an Object
\[F=\frac{\mu \,\,Mg}{\cos \theta +\mu \sin \theta }=force\,\,required\,to\,pull\,on\,object\] force required to pull an object \[W=F\,\,d=\frac{\mu \,\,Mg\,\,d}{\cos \theta +\mu \,\,\sin \,\theta }\]
Similarly, work done in pushing an object
\[W=\frac{\mu \,\,Mg\,\,d}{\cos \theta +\mu \,\,\sin \,\theta }\]
Work Done by a Variable Force
\[W=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{Fdx=}\]area under F-x curve with proper algebraic sign.
Work done by external force when spring is elongated from \[{{x}_{1}}to\,{{x}_{2}}\]
Work done in small displacement dx, dW = Fdx
Total work done, W=\[\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{Fdx=k\,\,\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{xdx}}\]
\[F=kx\]
The constant k is the spring constant or force constant.
\[W=\frac{1}{2}k{{x}_{2}}^{2}-\frac{1}{2}k{{x}_{1}}^{2}\]
Conservative Force
A force is said to be conservative, if the work done, by or against the force
(i) is independent of path and depends only on initial and final positions.
(ii) does not depend on the nature of path followed between the initial and final positions.
Examples of conservative force: All central forces are conservative like gravitational, electrostatic, elastic force, restoring force due to spring etc.
SPECIAL POINTS
(a) Work done along a closed path or in a cyclic process is zero. i.e.\[i.e.\,\,\oint{F.dx=0}\]
(b) If \[\overrightarrow{F}\] is a conservative force, then \[\overrightarrow{\Delta }\times \overrightarrow{F}=0\]
Non-conservative Force
A force is said to be non-conservative, if work done, by or against the force in moving a body depends upon the path between the initial and final positions.
The work done in a closed path is not zero in a non-conservative force field.
Examples of non-conservative force: Air resistance, viscous force etc.
Energy
The energy of a body is defined as the capacity of doing work or ability of the body to do work.
It is a scalar quantity.
The dimensional formula of energy is \[[M{{L}^{2}}{{T}^{-2}}]\]. It is the same as that of work. The unit of energy are the same as that of work Le,, joule in S. I. system and erg in CGS system.
Kinetic Energy
It is the energy possessed by a body by virtue of its motion. If v be the velocity acquired by the block after travelling a distance x,
then kinetic energy
\[K=W=Fx=m.a.x=\frac{1}{2}m{{v}^{2}}\] \[[\therefore {{v}^{2}}=2ax]\]
Work Energy Theorem for a Variable Force
The work done by the resultant force in displacing the particle from\[{{x}_{0}}\] to x is
\[W=\frac{1}{2}m{{v}^{2}}f-\frac{1}{2}m{{v}^{2}}_{i}\]
'The work done by the resultant force acting on a particle is equal to the change in the kinetic energy of the particle".
This equation represents work-energy (W.E.) theorem.
Relation Between Momentum and Kinetic Energy
\[P=\sqrt{2mE}\]
Potential Energy
The energy stored in a body or system by virtue of its configuration or its position is called potential energy.
Potential energy of a body at any height h from the earth's surface,
U=mgh
The potential energy is equal to negative of work done in shining an object from some reference position to a given position for conservative force.
\[\Delta U=-\int\limits_{i}^{f}{\overrightarrow{F}}.\overrightarrow{dr}\,\,or\,\,{{U}_{f}}-{{U}_{i}}=-\int\limits_{i}^{f}{\overrightarrow{F}}.\overrightarrow{dr}\]
The Potential Energy of a Spring
Potential energy of a compressed or stretched spring
\[U=\frac{1}{2}k{{x}^{2}}\]
Law of Conservation of Mechanical Energy
The sum of the potential energy and the kinetic energy is called the total mechanical energy.
Total mechanical energy of a system remains constant if only conservative forces are acting on a system of particles and the work done by all other forces is zero.
\[\Delta \Kappa +\Delta U=0\]
or \[{{K}_{f}}-{{k}_{i}}+{{U}_{f}}-{{U}_{i}}=0\]
or \[{{K}_{f}}+{{U}_{f}}={{K}_{i}}+{{U}_{i}}=\text{constant}\]
Equilibrium
A body is said to be in translatory equilibrium, if net force acting on the body is zero i.e., \[{{\overrightarrow{F}}_{net}}=0\]
If the force are conservative then, \[F=-\frac{dU}{dr}\]
For equilibrium,\[F=0.\]So, \[-\frac{dU}{dr}=0,\]or, \[\frac{dU}{dr}=0\]
At equilibrium position slope of \[U-r\]graph is zero or the potential energy is optimum (maximum or minimum or constant).
Law of Conservation of Energy:
"Energy cannot be created or destroyed, it may only be transformed from one form into another. As such the total amount of energy never changes".
Power
We define power as the rate at which work is being done.
Average power,\[{{P}_{av}}=\frac{Work\,\,done}{Time\,\,taken\,\,to\,\,do\,\,work}\]
\[=\frac{Total\,\,change\,\,in\,\,kinetic\,\,energy}{Total\,\,time\,\,in\,\,change}\]
If \[\Delta W\] is the amount of work done in the time interval \[\Delta t\] then.
\[Ins\tan \operatorname{taneous}\,\,power,p=\frac{\Delta W}{\Delta t}=\frac{{{W}_{2}}-{{W}_{1}}}{{{t}_{2}}-{{t}_{1}}}\]
\[p=\overrightarrow{F}.\overrightarrow{v}=Fv\,\,\cos \,\,\theta \]
Collisions
When exchange of momentum takes place between two physical bodies only due to their mutual interaction force. It is defined as collision between two bodies.

In all collisions, linear momentum is conserved.
i.e., \[{{m}_{1}}{{\overrightarrow{u}}_{1}}+{{m}_{2}}{{\overrightarrow{u}}_{2}}={{m}_{1}}{{\overrightarrow{v}}_{1}}+{{m}_{2}}{{\overrightarrow{v}}_{2}}\]
Newton's Law of Collision
According to Newton's experimental law of impact, the ratio of relative speed of separation after collision and the relative speed of approach before collision is a constant. This constant is called coefficient of restitution or coefficient of resilience. For a given pair of materials. It is denoted by e.
Coefficient of restitution,
\[e=\frac{{{\overrightarrow{v}}_{2}}-{{\overrightarrow{v}}_{1}}}{{{\overrightarrow{u}}_{1}}{{\overrightarrow{u}}_{2}}}=\frac{(velocity\,of\,separation\,after\,collision)}{velocity\,of\,approach\,\,before\,\,collision}\]
(i) e = 1, the collision is perfectly elastic.
(ii) e = 0, the collision is perfectly inelastic.
(iii) 0 < e < 1, the collision is inelastic.
In this case of elastic collision
2 Linear momentum is conserved.
In case of inelastic collision:
Perfectly Elastic or Head on Collision (Collision in One Dimension)
![]()
\[{{v}_{1}}=\left( \frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right){{u}_{1}}+2\left( \frac{{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right){{u}_{2}}\]
\[{{v}_{2}}=\left( \frac{2{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right){{u}_{1}}+\left( \frac{{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right){{u}_{2}}\]
Perfectly Inelastic Collision (Particles Stick After Collision)
Collision is said to be perfectly inelastic if both the particles stick together after collision and move with same velocity, say V.
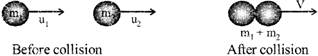
\[V=\frac{{{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}}{{{m}_{1}}+{{m}_{2}}}\]
Loss of kinetic energy during collision is \[\Delta \Kappa ={{\Kappa }_{i}}-{{K}_{f}}\] \[\Delta K=\frac{1}{2}\,\,\left[ \frac{{{m}_{1}}{{m}_{2}}}{({{m}_{1}}+{{m}_{2}})}\,\,{{({{u}_{1}}-{{u}_{2}})}^{2}} \right]\]
Inelastic Collision (Head on) Particles do not Stick After Collision
\[{{v}_{1}}=\frac{\left( {{m}_{1}}-e{{m}_{2}} \right)}{{{m}_{1}}+{{m}_{2}}}{{u}_{1}}+\frac{{{m}_{2}}(1+e)}{{{m}_{1}}+{{m}_{2}}}{{u}_{2}}\]
\[{{v}_{2}}=\frac{{{m}_{1}}(1+e)}{{{m}_{1}}+{{m}_{2}}}{{u}_{1}}+\frac{({{m}_{2}}-e{{m}_{1}})}{{{m}_{1}}+{{m}_{2}}}\]
Loss in kinetic energy, \[\Delta \Kappa ={{\Kappa }_{i}}-{{K}_{f}}\]
\[=\frac{1}{2}{{m}_{1}}{{u}^{2}}_{1}+\frac{1}{2}{{m}_{2}}\,\,{{u}_{2}}^{2}-\frac{1}{2}{{m}_{1}}{{v}^{2}}_{1}-\frac{1}{2}{{m}_{2}}{{v}^{2}}_{2}\]
\[\Rightarrow \,\,\,\,\,\,\,\,\,\Delta \Kappa =\frac{{{m}_{1}}{{m}_{2}}}{2({{m}_{1}}+{{m}_{2}})}{{({{u}_{1}}-{{u}_{2}})}^{2}}(1-{{e}^{2}})\]
You need to login to perform this action.
You will be redirected in
3 sec
