Heat and Temperature
Category : Railways
Heat and Temperature
TEMPERATURE
Temperature is defined as the degree of hotness or coldness of a body. Hot and cold are relative terms. According to kinetic theory of gases, temperature is a measure of average translational kinetic energy of a molecule i.e.,\[{{T}_{K}}\propto \](K.E) molecules.
It is a scalar quantity. Its S.I. unit is kelvin (K) with dimensions \[[{{M}^{0}}{{L}^{0}}{{T}^{0}}\theta ]\]
Measurement of Temperature
A branch of science which deals with the measurement of temperature of a substance is called thermometry. Thermometer is a device used to measure the temperature. Thermometer used for measuring very high temperatures are called pyrometer.
Relationship Between Different Scales of Temperature:
\[\frac{C-0}{100}=\frac{F-32}{212-32}=\frac{K-273.16}{373.16-273.16}\]
\[=\frac{R-0}{80-0}=\frac{Ra-460}{672-460}\]
\[T{}^\circ (K)=(t{}^\circ C+273.16)\]
Normal temperature of human body is \[310.15\,\,k(37{}^\circ C=98.6{}^\circ F)\]
STP or NTP implies 273.15 K \[(0{}^\circ C=32{}^\circ F)\]
Ideal-Gas Equation and Absolute Temperature
The equation, PV= nRT
where, n = number of moles in the sample of gas
R = universal gas constant;\[(its\,\,value\,\,is\,\,8.31\,\,J\,\,mo{{l}^{-1}}{{K}^{-1}})\] is known as ideal-gas equation
It is the combination of following three laws
(i) Boyle's law: When temperature is held constant, the pressure is inversely proportional to volume.
i.e.,\[P\propto \frac{1}{V}\](at constant temperature)
(ii) Charle's law: When the pressure is held constant, the volume of the gas is directly porportional to the absolute temperature.
i.e., V\[\propto \]T (at constant pressure)
(iii) Avogadro's law: When the pressure and temperature are kept constant, the volume is directly proportional to the number of moles of the ideal gas in the container.
i.e., V \[\propto \] n (at constant pressure and temperature)
Absolute Temperature
The lowest temperature of\[-2\text{ }73.16\,\,{}^\circ C\] at which a gas is supposed to have zero volume and zero pressure and at which entire molecular motion stops is called absolute zero temperature. A new scale of temperature starting with \[-273.16{}^\circ C\]by Lord Kelvin as zero. This is called Kelvin scale or absolute scale of temperature.
T (K)\[=t{}^\circ C+273.16\]
Thermal Expansion
The increase in the dimensions of a body due to the increase in its temperature is called thermal expansion. The thermal expansion of solid is classified as follows:
On increasing the temperature of a solid, its length increases. This increase in length of a solid on heating is called linear expansion. The fractional increase in length per "C rise in temperature is called coefficient of linear expansion.
Coefficient of linear expansion,\[\propto =\frac{\left( \frac{\Delta \ell }{\ell } \right)}{\Delta \Tau }=\frac{d\ell }{\ell .dt}\]
If \[\alpha \] is coefficient of linear expansion at \[{{t}_{1}}{}^\circ C\] then,
\[{{\ell }_{1}}\]= length of the rod at \[{{t}_{1}}{}^\circ C\]
\[{{\ell }_{2}}\]= length of the rod at \[{{t}_{2}}{}^\circ C\]
then, \[{{\ell }_{2}}={{\ell }_{1}}[1+\alpha \,\,({{t}_{2}}-{{t}_{1}})]\]
In increasing the temperature of a solid, its area increases. This increase in area is referred as superficial expansion. If the area of solid at temperature\[{{t}_{1}}{}^\circ C\]is a) and on heating the rod, the area becomes \[{{A}_{2}}\] at \[{{t}_{2}}{}^\circ C\] then,
\[{{A}_{2}}={{A}_{1}}[1+\beta \,\,({{t}_{2}}-{{t}_{1}})]\]
where\[\beta \]is called coefficient of superficial expansion at \[{{t}_{1}}{}^\circ C\]Coefficient of superficial expansion is defined as the fractional increase in area per \[{}^\circ C\] rise in temperature.
i.e.. Coefficient of areal expansion \[\beta =\frac{\Delta A/A}{\Delta \Tau }=\frac{dA}{A.dT}\]
In increasing the temperature of a solid, its volume increases. This increase in volume with increase in temperature is called cubical or volume expansion if \[{{V}_{1}}\]is the volume of a solid at temperature \[{{t}_{1}}{}^\circ C\]and on increasing the temperature to\[{{t}_{2}}{}^\circ C\] the volume becomes \[{{V}_{2}}\] then,
\[{{V}_{2}}={{V}_{1}}[1+\gamma \,\,({{t}_{2}}+{{t}_{1}})]\]
Where \[\gamma \]is coefficient of volume expansion at \[{{t}_{1}}{}^\circ C\]
Coefficient of volume expansion is defined as the fractional increase in volume per \[{}^\circ C\] rise in temperature.
i.e., Coefficient of volume expansion, \[\gamma =\frac{\Delta V/V}{\Delta \Tau }=\frac{DV}{V.dT}\]
Relation between coefficient of linear expansion (a), coefficient of superficial expansion (P) and coefficient of cubical expansion\[(\gamma )\]
\[\alpha =\frac{\beta }{2}=\frac{\gamma }{3}\Rightarrow \alpha :\beta :\gamma =1:2:3\]
Applications of Thermal Expansion in Solids
(i) Bimetallic strip: If two strips of different metals are welded Together to form a bimetallic strip, when heated uniformly it bends in the form of an arc, the metal with greater coefficient of linear expansion lies on convex side.

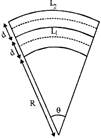
The radius of arc thus formed by bimetal is,
\[R=\frac{d}{\left( {{\alpha }_{2}}-{{\alpha }_{1}} \right)\,\,\left( {{t}_{2}}-{{t}_{1}} \right)}\]or \[R=\frac{d}{\left( {{\alpha }_{2}}-{{\alpha }_{1}} \right)\Delta t}\]
where \[\Delta t\]= temp. difference between the two ends.
d = thickness of each strip
\[{{\alpha }_{1}}\]and \[{{\alpha }_{2}}\] are coefficients of linear expansion of two
different metals.
(ii) Thermal stress in a rigidly fixed rod:
Thermal strain =\[\frac{{{\ell }_{2}}-{{\ell }_{1}}}{{{\ell }_{2}}}=\alpha \,\,({{t}_{2}}-{{t}_{1}})\]
In elasticity. Young's modulus \[=\frac{\text{stress}}{\text{strain}}\]
\[\therefore \]Thermal stress \[=Y\alpha \,\,({{t}_{2}}-{{t}_{1}})\]
Tensile strain\[\simeq \alpha \Delta t\]
(iii) Effect of temperature on pendulum clock:
Change in time period, \[\Delta \Tau ={{T}_{2}}-{{T}_{1}}=\frac{1}{2}\,\,\alpha .\Delta \theta .{{T}_{1}}\]
Expansion of liquid
When a liquid is heated, its container also expands. The observed expansion of the liquid is called apparent expansion which is different from the real expansion of the liquid. Coefficient of apparent expansion. The coefficient of apparent expansion of the liquid is given by
\[{{\gamma }_{a}}=\frac{\text{Real}\,\,\text{increase}\,\,\text{in}\,\,\text{volume}}{\text{Original}\,\,\text{volume }\!\!\times\!\!\text{ rise}\,\,\text{in}\,\,\text{temperature}}\]
Coefficient of real expansion. The coefficient of real expansion of the liquid is given by
\[{{\gamma }_{r}}=\frac{\operatorname{Re}al\,\,increase\,\,in\,\,volume}{Original\,\,volume\times rise\,\,in\,\,temperature}\]
It can be proved that \[{{\gamma }_{r}}={{\gamma }_{a}}+{{\gamma }_{g}}\]
where\[{{\gamma }_{g}}\]is coefficient of cubical expansion of glass (material) of the containe.
Change in Density with Temperature
Suppose m is the mass of a solid which is at a given temperature In occupies a volume V so that density at \[0{}^\circ C\] is \[{{d}_{0}}=\frac{m}{V}\]
Now, if the temperature is increased by\[t{}^\circ C\], mass will remain unchanged but due to thermal expansion volume increases so that, \[V'=V\,\,(1+\gamma \Delta t)\]
Now density \[{{d}_{1}}={{d}_{0}}(1-\gamma \Delta t)\]
Here \[\gamma \]is coefficient of cubical expansion of the substance at\[0{}^\circ C\],
Anomalous Expansion of Water
Almost all liquids expand on heating but water when heated from \[0{}^\circ C\] to \[4{}^\circ C\]its volume decreases and hence density increases until its temperature reaches\[4{}^\circ C\]. Its density is maximum at\[4{}^\circ C\]on further heating its density decreases. This behaviour of water is called anomalous behaviour of water.
HEAT
Heat is a form of energy which causes sensation of hotness or coldness. It is transferred between two or more systems or a system and its surroundings by virtue of temperature difference. The flow of heat is always from higher temperature to lower temperature.
No heat flows from one body to other, when both the bodies are at the same temperature. The two bodies are said to be in thermal equilibrium.
The SI unit of heat is joule. Its CGS unit is calorie, 1 cal =4.2 joule
Specific heat Capacity
Specific heat capacity: It is the amount of heat energy needed to raise the temperature of unit mass of substance by \[1{}^\circ C\](or 1K).
It is denoted by s or c.
If the temperature of a substance of mass m changes from T to T + dT when it exchanges an amount of heat dQ with its surroundings, then its specific heat capacity is given by
\[c=\frac{1}{m.}\,\,\frac{dQ}{dT}\]
Unit of specific heat capacity:
CGS unit of specific heat capacity is \[cal/g{}^\circ C\]
SI unit of specific heat capacity is joule/kg K
For example, the specific heat capacity of water is:
0
Definition of one calorie: Amount of heat required to raise temperature of one gram of water from \[14.5{}^\circ C\]to \[15.5{}^\circ C\] is known as one calorie.
Gram specific heat capacity "c": The amount of heat required to raise the temperature of the I gram substance by \[1{}^\circ C\]is known as "gram specific heat".
Molar specific heat capacity" C": The molar heat capacity C is the heat required to raise the temperature ofl mole of a gas by \[1{}^\circ C\](or 1 K)." Heat required to raise the temperature of u gram- mole of a substance by \[\Delta \theta {}^\circ C,\]
\[C=\frac{\Delta Q}{n\Delta \Tau }\]
Its SI unit is \[J\,\,mo{{l}^{-1}}{{K}^{-1}}\] and CGS unit cal \[mo{{l}^{-1}}{}^\circ {{C}^{-1}}\]
Thermal or heat capacity: It is the quantity of heat required to raise the temperature of the whole of that substance through\[1{}^\circ C\]. The thermal capacity of mass m of the whole of substance of specific heat capacity s is equal to (ms) kilocalorie i.e., Thermal capacity = mass \[\times \] specific heat capacity
Water equivalent of a body: The thermal capacity of a body (ms) represents also its water equivalent, since the specific heat of water is unity.
The water equivalent of a body is the amount of water that absorbs or gives out the same amount of heat as is done by the body when heated or cooled through\[1{}^\circ C\].
Mass of water having the same thermal capacity as the body is called the water equivalent of the body
W= mass \[\times \] specific heat capacity
Its SI unit is Kg and CGS unit g.
Calorimetry
The branch of physics that deals with the measurement of heat is called calorimetry. A device in which heat measurement can be done is called calorimeter.
Principle of Calorimetry or Law of Mixture
According to the principle of calorimetry, Heat lost = heat gained
Heat lost or gained by a body is given by,
\[Q=m\times C\times ({{\theta }_{2}}-{{\theta }_{1}})\]
Principle of calorimetry represents the law of conservation of heat energy. Temperature of mixture (T) is always \[\ge \] lower temperature \[({{T}_{L}})\] and \[\le \]higher temperature\[({{T}_{H}})\],
\[{{T}_{L}}\le T\le {{T}_{H}}\]
Latent Heat or Hidden Heat
When state of a substance changes, change of state takes place at constant temperature (m.pt. or b.pt.) heat is released or absorbed and is given by,
Q=mL
where L is latent heat. Heat is absorbed if solid converts into liquid (at m.pt.) or liquid converts into vapour (at b.pt.) and is released if liquid converts into solid or vapours converts into liquid.
The SI unit of latent heat is J/kg
Latent heat of fusion: The quantity of heat (in kilocalorie) required to change its 1 kg mass from solid to liquid state at its melting point is called latent heat of fusion. For ice latent heat of fusion = 80 kilo cal/kg.
Latent heat of vaporization: It is the quantity of heat required to change its 1 kg mass from liquid to vapour state at its boiling point. For water latent heat of vaporisation = 536 kilocal/kg.
Change of State
Some common changes of states:
(i) Melting: When heat is supplied, solid substance changes into liquid, this change of state of substance is called melting.
\[\text{Solid}\,\,\xrightarrow{Heat}\,\,\text{Liquid}\]
The temperature at which the solid and the liquid states of a substance coexist in thermal equilibrium with each other is called its melting point.
(ii) Freezing: When heat is released, liquid changes into solid, this change of state of substance is called freezing.
\[Liduid\,\,\xrightarrow{CooL}\,\,Solid\]
(iii) Condensation: When vapour is cooled, it changes into liquid, this change of state is called condensation
\[Vapour\,\,\xrightarrow{CooL}\,\,Liquid\]
(iv) Evaporation: Conversion of liquid into gaseous state at all the temperatures is called evaporation or boiling.
\[Liquid\,\,\xrightarrow{Heat}\,\,Vapour\]
The temperature at which the liquid and vapour states of a substance coexsist in thermal equilibrium with each other is called its boiling point.
(v) Sublimation: It is the conversion of a solid directly into vapours.
\[Solid\,\,\xrightarrow{Heat}\,\,Vapour\]
Sublimation takes place when boiling point is less than the melting point.
Heating Curve
If to a given mass (m) of a solid, heat is supplied at constant rate and a graph is plotted between temperature and time, the graph is as shown in fig. and is called heating curve. From this curve it is clear that:
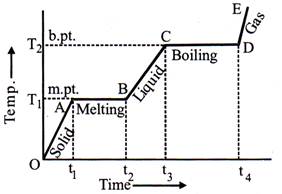
Regelation: The phenomenon in which ice-melts when pressure is increased and again freezes when pressure is removed is called regelation.
Heat Transfer
Conduction
Conduction is that mode of transmission of heat in which heat is transferred from a region of higher temperature to a region of lower temperature by the aid of particles of the body without their actual migration. Conduction requires material medium.
Variable state and steady state:
When one end of a rod is heated, then initially the temperature of various points of the rod changes continuously and the rod is said to exist in a variable state. After some time, a state is reached, when the 6m temperature of each cross-section becomes steady. this state is known as steady state.
If rod is in contact with atmosphere or surroundings and it is heated at one end then distance versus temperature curve is as shown in fig. alongside.
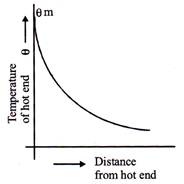
And if rod is insulated with surroundings then graph is straight line. Temperature gradient: The rate of change of temperature with distance between two isothermal surfaces is called temperature gradient
If the temperature of the isothermal surfaces be \[\theta \] and\[\theta -\Delta \theta \] and perpendicular distance between them is\[\Delta x\] then,
Temperature gradient between them
\[\text{=}\frac{\text{change}\,\,\text{in}\,\,\text{temperature}}{\text{Distance}\,\,\text{between}\,\,\text{two}\,\,\text{surfaces}}\]\[=\frac{(\theta -\Delta \theta )}{\Delta x}=-\frac{\Delta \theta }{\Delta x}\]
The negative sign show that temperature \[\theta \] decreases as the distance x increases in the direction of heat flow.
Unit in SI System \[{}^\circ C/metre\]
THERMAL CONDUCTIVITY
Heat current, \[H=\frac{Q}{t}\]
It has been found experimentally that in steady state, heat current will be
(a) proportional to the area of the cross-section A of the rod.
(b) proportional to temperature difference \[({{\theta }_{1}}-{{\theta }_{2}})\]
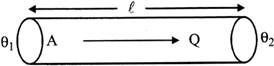
Thus we find that
\[\frac{Q}{t}\,\,\alpha \,\,\frac{A\,\,\left( {{\theta }_{1}}-{{\theta }_{2}} \right)}{\ell }\] or \[H=\frac{K\,\,A\,\,\left( {{\theta }_{1}}-{{\theta }_{2}} \right)}{\ell }\]
where K. is a constant of proportionality called the thermal conductivity of the substance.
Coefficient of thermal conductivity (K): The coefficient of thermal conductivity, K, of a material is defined as the amount of heat that flowing per second through a rod of that material having unit length and unit area of cross-section in the steady state, when the difference of temperature between two ends of the rod is \[1{}^\circ C\]and flow of heat is perpendicular to the end faces of the rod.
Unit of coefficient of thermal conductivity in SI system is watt/m-K
Dimensions: \[[ML{{T}^{-3}}{{\theta }^{-1}}]\]
For a perfect conductor thermal conductivity K is infinite and for a perfect insulator K is zero.
Thermal Resistance: The thermal resistance of a body is a. measure of its obstruction to the flow of heat through it. It is defined as the ratio of temperature difference to the heat current (= rate of flow of heat)
Now, if temperature difference = \[({{\theta }_{1}}-{{\theta }_{2}})\]
\[\ell \]= length of rod
Heat current, \[H=\frac{Q}{t};\] A = area of cross section of rod
\[\therefore \] \[{{R}_{Th}}=\frac{{{\theta }_{1}}-{{\theta }_{2}}}{H}=\frac{{{\theta }_{1}}-{{\theta }_{2}}}{H}=\frac{{{\theta }_{1}}-{{\theta }_{2}}}{(Q/t)}=\frac{{{\theta }_{1}}-{{\theta }_{2}}}{KA\,\,({{\theta }_{1}}-{{\theta }_{2}})/\ell }=\frac{\ell }{KA}\]
or \[{{R}_{Th}}=\frac{\Delta \theta }{H}=\frac{\ell }{KA}\]
Unit in SI system: Kelvin sec/ kilojoule
Combination of Metallic Conductors
Equivalent thermal conductivity in series combination of conductors
\[{{K}_{eq}}=\frac{{{\ell }_{1}}+{{\ell }_{2}}}{\frac{{{\ell }_{1}}}{{{K}_{1}}}+\frac{{{\ell }_{2}}}{{{K}_{2}}}}\]
\[If\,\,\,\,{{\ell }_{1}}={{\ell }_{2}}=\ell \,\,\,\,\,\,\,\,\,\,\,;{{K}_{eq}}=\frac{2{{K}_{1}}{{K}_{2}}}{{{K}_{1}}+{{K}_{2}}}\]
If we have more than two slabs in the compound slab.
The total thermal resistance of the slabs connected in series
\[{{R}_{eq}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+.....+{{R}_{n}}\]
Equivalent thermal conductivity in parallel combination of conductors
\[\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}\]
For more than two slabs, we have
\[\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}+....+\frac{1}{{{R}_{n}}}\]
\[{{K}_{eq}}=\frac{{{k}_{1}}{{A}_{1}}+{{K}_{2}}{{A}_{2}}}{{{A}_{1}}+{{A}_{2}}}\]
If, \[{{A}_{1}}={{A}_{2}},\]then \[{{K}_{eq}}=\frac{{{K}_{1}}+{{K}_{2}}}{2}\]
Convection
Convection like conduction requires a material medium. It is the process in which heat is transferred from one place to other by actual movement of' heated material particles It is possible only in fluids. The type of convection which results from difference in densities is called natural convection. For example, a fluid in a container heated through its bottom. However, if a heated fluid is forced to move by a blower, fan or pump, the process is called forced convection. The rate of heat convection from an object is proportional to the temperature difference (A9) between the object and convective fluid and the area of contact A,
i.e., \[{{\left[ \frac{dQ}{dt} \right]}_{convection}}=hA\Delta \theta \]
where, h represents a constant of proportionality called convection coefficient and depends on the properties of fluid such as density, viscosity, specific heat and thermal conductivity.
Radiation
When a body is heated and placed in vacuum, it loses heat even when there is no medium surrounding it. The process by which heat is lost in this case is called radiation. This does not require the presence of any material medium,
Radiation has the following properties:
(a) Radiant energy travels in straight line and when some object is placed in the path, it's shadow is formed at the detector.
(b) It is reflected and refracted or can be made to interfere. The reflection or refraction are exactly as in case of light.
(c) It can travel through vacuum.
(d) Intensity of radiation follows the law of inverse square.
(e) Thermal radiation can be polarised in the same way as light by transmission through a nicol prims.
|
Radiation |
Wavelength range |
|
\[\gamma \]-rays |
\[{{10}^{-10\,}}m\,\,to\,\,{{10}^{-14}}\,\,m\] |
|
X-rays |
\[{{10}^{-9}}m\,\,to\,\,6\times {{10}^{-12}}m\] |
|
Ultra violet rays |
\[3.8\times {{10}^{-7}}m\,\,to\,\,6\times {{10}^{-10}}m\] |
|
Visible rays |
\[7.8\times {{10}^{-7}}m\,\,to\,\,3.8\times {{10}^{-7}}m\] |
|
Infrared rays |
\[{{10}^{-3}}m\,\,to\,\,7.8\times {{10}^{-7}}m\] |
|
Microwaves |
\[0.3\,\,m\,\,to\,\,{{10}^{-3}}m\] |
|
Radiowaves |
Few Km to 0.3 m |
Absorption coefficient or absorptance:
\[a=\frac{{{Q}_{r}}}{Q}\,\,\frac{Quantity\,\,of\,\,radiant\,\,energy\,\,absorbed\,by\,the\,body}{\begin{align}
& Quantity\,\,of\,\,radiant\,\,energy\,\,incident\,\,on \\
& the\,\,surface\,\,of\,\,the\,\,body \\
\end{align}}\]
Reflection coefficient or reflectance:
\[r=\frac{{{Q}_{r}}}{Q}\,\,\frac{Quantiy\,\,of\,\,radiant\,\,energy\,\,reflected}{\begin{align}
& Quantity\,\,of\,\,radiant\,\,energy\,\,incident\,\,on \\
& the\,\,surface\,\,of\,\,the\,\,body \\
\end{align}}\]
Transmission coefficient or transmittance:
\[t=\frac{{{Q}_{t}}}{Q}\frac{Quantity\,\,of\,\,radiant\,\,energy\,\,transmitted\,\,by\,\,the\,\,body}{\begin{align}
& Quantity\,\,of\,\,radiant\,\,energy\,\,incident\,\,on \\
& the\,\,surface\,\,of\,\,the\,\,body \\
\end{align}}\]and \[{{Q}_{a}}+{{Q}_{r}}+{{Q}_{t}}=Q\]
\[\therefore \] \[\frac{{{Q}_{a}}}{Q}+\frac{{{Q}_{r}}}{Q}+\frac{{{Q}_{t}}}{Q}=1\] and also, \[a+r+t=1\]
Diathermanous substances: The substances which can transmit the radiant heat incident upon their surfaces are called diathermanous substances, \[(t\ne 0)\]
Athermanous substances: The substances which cannot transmit the radiant heat incident upon their surfaces are called athermanous substances, (t = 0). Water vapour and carbon dioxide are athermanous.
Emissive power (e): For a given surface it is defined as the radiant energy emitted per sec per unit area of the surface.
Spectral emissive power\[({{e}_{\lambda }})\]: If we consider emissive power of a surface for a particular wavelength instead of all wavelengths, it is called spectral emissive power and is represented by
Total emissive power, \[e=\int\limits_{0}^{\infty }{{{e}_{\lambda }}}d\lambda \]
Emissive power of a surface depends on its nature and temperature. It is maximum for a perfectly black body and minimum for a smooth shining body.
Unit in SI system \[W/{{m}^{2}}\]
Absorptive power (a): Absorptive power of a surface is defined as the ratio of the radiant energy absorbed by it in a given time to the total radiant energy incident on it in the same time. If Q calorie of heat fall on the surface and Q' calorie out of it are absorbed, the 0' absorptive power of the surface is given by, \[a=\frac{Q'}{Q}\]
For a perfectly black body, absorptive power is maximum and unity. It has no unit and dimensions.
Spectral absorptive power\[\left( {{a}_{\lambda }} \right)\]: Spectral absorptive power is defined as the ratio of the radiant energy of a given wavelength absorbed by a given surface in a given time to the total radiant energy of that wavelength incident in the same time on the same surface within a unit wavelength range.
Total absorptive power, \[a=\int_{0}^{\infty }{a\lambda d\lambda }\]
Absolute emissivity: The emissivity e of a surface is defined as the quantity of heat radiated per second by one unit area of its surface when its temperature is 1°C above the surroundings.
Relative emissivity (e): It is defined as the ratio of radiant energy emitted per unit time per unit surface area of a body at a given temperature (E) to the radiant energy emitted per unit time per unit surface area of a perfectly black body \[({{E}_{b}})\] at the same temperature.
i.e., \[e=\frac{E}{{{E}_{b}}}\]
Different bodies
(i) If a = t =0 and r =1\[\to \]body is perfect reflector
(ii) If r = t = 0 and a =1\[\to \]body is perfectly black body
(iii) If a = r = 0 and t =1\[\to \]body is perfect transmitter
(iv) If t=0\[\Rightarrow \]r+ a= 1 or a= 1-r, i.e., good reflectors are bad absorbers.
Perfectly Black Body
A black body is defined as one that will completely absorb all the radiations of whatever wavelength which falls on it.
For perfectly black body, \[{{a}_{\lambda }}=1\]
Properties of perfectly black body:
(i) A perfectly black body absorbs all the radiant heat incident upon it. (i. e. a= 1)
(a) A perfectly black body does not reflect or transmit the radiant heat incident upon it. (i. e. t = 0, r = 0)
(iii) The coefficient of emission of a perfectly black body is 1. It is very good emitter of heat.
(iv) A perfectly black body does not exist in nature.
For practical purposes lamp black is treated as a perfectly black body as its coefficient of absorption is nearly 0.98.
Wien's Displacement Law according to Wien's displacement law \[{{\lambda }_{m}}\times T=b\]
Here, constant b is known as Wien's constant
Stefan's Law of Heat Radiation
\[E\,\,\alpha \,\,{{T}^{4}}\]
The energy (\[{{E}_{\max }}\]) emitted corresponding to the wavelength of maximum emission\[({{\lambda }_{m}})\] increases with the fifth power of the absolute temperature of the black body.
\[i.e.,\,\,{{E}_{\max }}\propto {{T}^{5}}\]
It is known as Wien's fifth power taw.
Solar Constant
Solar constant, \[S=\frac{E{{R}^{2}}}{{{r}^{2}}}\]
But, E \[=\sigma {{T}^{4}}(according\,\,to\,\,Stefan's\,\,law,)\]
\[\therefore S=\frac{\sigma {{T}^{4}}{{R}^{2}}}{{{r}^{2}}}\,\,or\,\,{{T}^{4}}=\frac{S{{r}^{2}}}{\sigma {{R}^{2}}}\,\,or\,\,T=\left[ \frac{S\times {{r}^{2}}}{\sigma \times {{R}^{2}}} \right]\]
substituting these values above, we get T, the surface
Temperature of the Sun. It comes out to be equal to 5791 K. In this the surface temperature of Sun has been estimated.
Kirchhoffs Law of Heat Radiation
At any given temperature and for radiations of the same wevelength the ratio of the emissive power \[({{e}_{\lambda }})\]to the absorptive power\[({{a}_{\lambda }})\] is the same for all substances and is equal to the emissive power of a perfectly black body\[({{E}_{\lambda }})\]
\[i.e.,\,\,\,\frac{{{e}_{\lambda }}}{{{a}_{\lambda }}}=const.={{E}_{\lambda }}\]
Also, absorptive power of a body is equal to its emissivity.
\[i.e.,\,\,{{a}_{x}}=\varepsilon \left[ \because \frac{{{e}_{\lambda }}}{{{E}_{\lambda }}}=\varepsilon \right]\]
Stefan Boltzmann Law of Radiation
According to Stefan Boltzmann law, the quantity of heat energy radiated in one second per unit area of a perfectly black body is directly proportional to the fourth power of its absolute temperature.
i.e. \[{{E}_{b}}\propto {{T}^{4}}\] or \[{{E}_{b}}=\sigma {{T}^{4}}\]
where \[\sigma \] is a universal constant known as Stefan-Boltzmann
constant and T is its temperature on absolute scale. The measured value of \[\sigma \] is \[5.67\times {{10}^{-8}}W/{{m}^{2}}-{{K}^{4}}\,\,or\,\,\sigma =5.67\times {{10}^{-5}}erg/c{{m}^{2}}s{{K}^{4}}\]The\[e{{q}^{n}}{{E}_{b}}=\sigma {{T}^{4}}\] is called the Stefan-Boltzmann law.
Total energy radiated by the surface of a body in time t
\[Q=\varepsilon \,\,\sigma \,\,A\,\,t\,\,{{T}^{4}}\]
Cooling of a body by radiation
Consider a perfectly black body of absolute temperature T is surrounded by another black body at absolute temperature\[{{T}_{0}}\]. Let, the surface area of the perfectly black body = A
The rate of loss of heat of the perfectly black body
\[\frac{dQ}{dt}=\varepsilon \sigma A\,\,({{T}^{4}}-T_{0}^{4})\]
Let, the emissivity of an ordinary body =\[\varepsilon \]
The rate of loss of heat of the ordinary body
\[\frac{dQ}{dt}=A\,\,\varepsilon \,\,\sigma \,\,({{T}^{4}}-T_{0}^{4})\,\,J/sec.\]
\[Rate\,\,of\,\,fall\,\,of\,\,temperature\,\,\frac{d\theta }{dt}=\frac{A\,\,e\,\,\sigma \,\,\left[ {{T}^{4}}-T_{0}^{4} \right]}{msJ}\,\,cal/\sec \]
Newton's law of cooling
The rate of cooling of a body (rate of loss of heat) is directly proportional to the excess of temperature of the body over the surroundings, provided that this excess is small and loses of heat by radiation only.
If\[\theta \]and\[{{\theta }_{0}}\]are the temperatures of the body and its surroundings respectively, then according to Newton's law of cooling,
Rate of loss of heat, \[-\frac{dQ}{dt}\,\,\propto \,(\theta -{{\theta }_{0}})\]
The negative sign indicates that the amount of heat is decreasing with time.
\[-\frac{dQ}{dt}=k(\theta -{{\theta }_{0}})\]
where k is the constant of proportionality.
Rate of fall of temperature
\[-\frac{dQ}{dt}=\frac{k}{m.s}\,\,(\theta -{{\theta }_{0}})\]
i.e. \[-\frac{d\theta }{dt}\,\,\alpha \,\,\left( \theta -{{\theta }_{0}} \right)\] (m and s are constant)
Thus, Newton's law of cooling can also be stated as,
The rate of fall of temperature of a body is directly proportional to excess of temperature of the body over the surroundings, provided that excess is small.
You need to login to perform this action.
You will be redirected in
3 sec
