Triode as an Amplifiers
Category : JEE Main & Advanced
Amplifier is a device by which the amplitude of variation of ac signal voltage / current/ power can be increased
(1) The signal to be amplified \[({{V}_{i}})\] is applied in the grid circuit and amplified output is obtained from the plate circuit
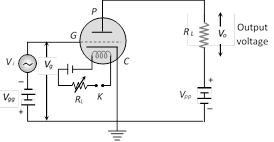
(2) The voltage at grid is the sum of signal \[{{V}_{i}}\] and grid bias \[{{V}_{gg}}\]. \[{{V}_{g}}={{V}_{gg}}+{{V}_{i}}\]
(3) Small change in grid voltage results in a large change in plate current so results in a large change in voltage across \[{{R}_{L}}\,({{V}_{0}}={{i}_{p}}{{R}_{L}}\,\Rightarrow \,\Delta {{V}_{0}}=\Delta {{i}_{p}}{{R}_{L}})\]
(4) The linear portion of the mutual characteristic with maximum slope is chosen for amplification without distortion.
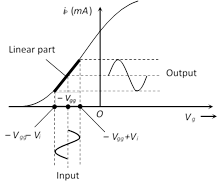
(i) For the positive half cycle of input voltage \[({{V}_{i}})\] : \[{{V}_{g}}\] becomes less negative, so \[{{i}_{p}}\] increases
(ii) For the negative half cycle of input voltage \[({{V}_{i}})\] : \[{{V}_{g}}\] becomes more negative, so \[{{i}_{p}}\] decreases
(iii) The phase difference between the output signal and input signal is \[{{180}^{o}}\] (or \[\pi \])
(5) Voltage amplification
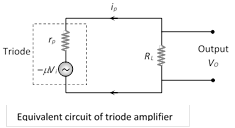
Current through the load resistance is given by \[{{i}_{p}}=-\frac{\mu {{V}_{i}}}{{{r}_{p}}+{{R}_{L}}}\,\] \[\Rightarrow \,{{V}_{0}}={{i}_{p}}{{R}_{L}}=\frac{-\,\mu {{V}_{i}}{{R}_{L}}}{{{r}_{p}}+{{R}_{L}}}\] \[\Rightarrow \] Voltage gain \[=\frac{{{V}_{0}}}{{{V}_{i}}}=-\frac{\mu {{R}_{L}}}{{{r}_{p}}+{{R}_{L}}}\] Numerically \[A=\frac{\mu {{R}_{L}}}{{{r}_{p}}+{{R}_{L}}}=\frac{\mu }{1+\frac{{{r}_{p}}}{{{R}_{L}}}}\]
(i) If \[{{R}_{L}}=\,\,\infty \,\,\Rightarrow A\] will be maximum and \[{{A}_{\max }}=\mu \] (Practically \[A<\mu \])
(ii) If \[{{r}_{p}}={{R}_{L}}\Rightarrow A=\frac{\mu }{2}\]
(iii) Power at load resistance \[P={{i}_{p}}{{V}_{0}}=i_{p}^{2}{{R}_{L}}\]
Condition for maximum power \[{{R}_{L}}={{r}_{p}}\] \[\therefore \] \[{{P}_{\max }}={{\left( \frac{\mu {{V}_{i}}}{{{R}_{L}}+{{R}_{L}}} \right)}^{2}}\times {{R}_{L}}=\frac{{{\mu }^{2}}V_{i}^{2}}{4{{R}_{L}}}\]
You need to login to perform this action.
You will be redirected in
3 sec
