Gay-Lussacs Law (Amonton's law)
Category : JEE Main & Advanced
(1) In 1802, French chemist Joseph Gay-Lussac studied the variation of pressure with temperature and extende the Charle’s law so, this law is also called Charle’s-Gay Lussac’s law.
(2) It states that, “The pressure of a given mass of a gas is directly proportional to the absolute temperature \[(={{\,}^{o}}C+273)\] at constant volume.”
Thus, \[P\propto T\] at constant volume and mass
or \[P=KT=K(t{{(}^{o}}C)+273.15)\] (where K is constant)
\[K=\frac{P}{T}\] or \[\frac{{{P}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}}{{{T}_{2}}}=K\] (For two or more gases)
(3) If \[t={{0}^{o}}C\], then \[P={{P}_{0}}\]
Hence, \[{{P}_{0}}=K\times 273.15\]
\[\therefore \] \[K=\frac{{{P}_{0}}}{273.15}\] \[P=\frac{{{P}_{0}}}{273.15}[t+273.15]={{P}_{0}}\left[ 1+\frac{t}{273.15} \right]={{P}_{0}}[1+\alpha t]\]
where \[{{\alpha }_{P}}\] is the pressure coefficient,
\[{{\alpha }_{P}}=\frac{P-{{P}_{0}}}{t{{P}_{0}}}=\frac{1}{273.15}=3.661\times {{10}^{-3}}{{\,}^{o}}{{C}^{-1}}\]
Thus, for every \[{{1}^{o}}\] change in temperature, the pressure of a gas changes by \[\frac{1}{273.15}\left( \approx \frac{1}{273} \right)\] of the pressure at \[{{0}^{o}}C\].
(4) This law fails at low temperatures, because the volume of the gas molecules be come significant.
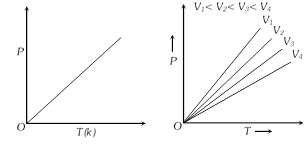
(5) Graphical representation of Gay-Lussac's law : A graph between P and T at constant V is called isochore.
You need to login to perform this action.
You will be redirected in
3 sec
