NEET Physics Two Dimensional Motion Time of Flight

Time of Flight Time of flight: The total time taken by the projectile to go up and come down to the same level from which it was projected is called time of flight. For vertical upward motion \[0 =u\,sin\,\,\theta \,gt\Rightarrow t=\text{ }(u\,sin\,\theta /g)\] Now as time taken to go up is equal to the time taken to come down so Time of flight \[T=2t=\frac{2u\,\sin \theta }{g}\] (i) Time of flight can also be expressed as: \[T=\frac{2.{{u}_{y}}}{g}\] (where \[{{u}_{y}}\] is the vertical component of initial velocity). (ii) For complementary angles of projection \[\theta \] and \[9{{0}^{o}}\theta \] (a) Ratio of time of flight \[=\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{2u\,\sin \theta /g}{2u\,\sin (90-\theta )/g}=\tan \theta \Rightarrow \frac{{{T}_{1}}}{{{T}_{2}}}=\tan \theta \] (b) Multiplication of time of flight = \[{{T}_{1}}{{T}_{2}}=\frac{2u\sin \theta }{g}\frac{2u\cos \theta }{g}\Rightarrow {{T}_{1}}{{T}_{2}}=\frac{2R}{g}\] (iii) If \[{{t}_{1}}\] is the time taken by projectile to rise upto point p and t2 is the time taken in falling from point p to ground level then  \[{{t}_{1}}+{{t}_{2}}=\frac{2u\sin \theta }{g}=\] time of flight or \[u\sin \theta =\frac{g({{t}_{1}}+{{t}_{2}})}{2}\] and height of the point p is given by \[h=u\sin \theta \,{{t}_{1}}-\frac{1}{2}gt_{1}^{2}\] \[h=g\frac{({{t}_{1}}+{{t}_{2}})}{2}{{t}_{1}}-\frac{1}{2}gt_{1}^{2}\] by solving \[h=\frac{g\,{{t}_{1}}{{t}_{2}}}{2}\] (iv) If B and C are at the same level on trajectory and the time difference between these two points is \[{{t}_{1}}\], similarly A and D are also at the same level and the time difference between these two positions is \[{{t}_{2}}\] then \[t_{2}^{2}-t_{1}^{2}=\frac{8h}{g}\] Sample problems based on time of flight Problem 20. For a given velocity, a projectile has the same range R for two angles of projection if t1 and t2 are the times of flight in the two cases then [KCET 2003] (a) \[{{t}_{1}}{{t}_{2}}\propto \,{{R}^{2}}\]   (b) \[{{t}_{1}}{{t}_{2}}\propto \,R\]      (c) \[{{t}_{1}}{{t}_{2}}\propto \,\frac{1}{R}\]        (d) \[{{t}_{1}}{{t}_{2}}\propto \,\frac{1}{{{R}^{2}}}\] Solution: (b) As we know for complementary angles \[{{t}_{1}}{{t}_{2}}=\frac{2R}{g}\] \ \[{{t}_{1}}{{t}_{2}}\propto R\]. Problem 21. A body is thrown with a velocity of 9.8 m/s making an angle of \[{{30}^{o}}\] with the horizontal. It will hit the ground after a time [JIPMER 2001, 2002; KCET (Engg.) 2001] (a) 1.5 s             (b) 1 s               (c) 3 s                (d) 2 s Solution: (b) \[T=\frac{2u\sin \theta }{g}=\frac{2\times 9.8\times \sin {{30}^{o}}}{9.8}=1\,\,\sec \] Problem 22. Two particles are separated at a horizontal distance x as shown in figure. They are projected at the same time as shown in figure with different initial speed. The time after which the horizontal distance between the particles become zero is [CBSE PMT 1999] 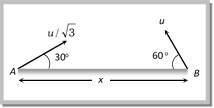(a) \[u/2x\]         (b) \[x/u\]                       (c) \[2u/x\]         (d) \[u/x\] Solution: (b) Let \[{{x}_{1}}\,\,and\,\,{{x}_{2}}\] are the horizontal distances travelled by particle A and B respectively in time t. \[{{x}_{1}}=\frac{u}{\sqrt{3}}.\cos 30{}^\circ \times t\]       ?.. (i)                      and        \[{{x}_{2}}=u\cos {{60}^{o}}\times t\]      ?? (ii) \[{{x}_{1}}+{{x}_{2}}=\frac{u}{\sqrt{3}}.\cos {{30}^{o}}\times t+u\cos {{60}^{o}}\times t=ut\]  \[\Rightarrow \,\,\,x=ut\] \[\therefore \,\,t=x/u\] Problem 23. A particle is projected from a point O with a velocity u in a direction making an angle a upward with the horizontal. After some time at point P it is moving at right angle with its initial direction of projection. The time of flight from O to P is (a) \[\frac{u\sin \alpha }{g}\]       (b) \[\frac{u\,\text{cosec}\alpha }{g}\]      (c) \[\frac{u\tan \alpha }{g}\]       (d) \[\frac{u\sec \alpha }{g}\] Solution: (b) When body projected with initial velocity \[\overrightarrow{u}\]by making angle \[\alpha \]with the horizontal. Then after time t, (at point P) it?s direction is perpendicular to \[\overrightarrow{u}\]. Magnitude of velocity at point P is given by \[v=u\cot \alpha .\] (from sample problem no. 9) For vertical motion: Initial velocity (at point O)\[=u\sin \alpha \] 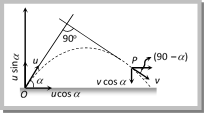Final velocity (at point P) \[=-\,v\cos \alpha \]\[=-u\cot \alpha \,\,\cos \alpha \] Time of flight (from point O to P) = t Applying first equation of motion \[v=u-g\,t\]             \[-\,u\cot \alpha \,\cos \alpha \,=\,u\sin \alpha -g\,t\]            \ \[t=\frac{u\sin \alpha +u\cot \alpha \,\cos \alpha }{g}\]\[=\frac{u}{g\sin \alpha }\left[ {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha  \right]\]\[=\frac{u\,\,\text{cosec}\alpha }{g}\] Problem 24. A ball is projected upwards from the top of tower with a velocity 50 ms?1 making angle 30o with the horizontal. The height of the tower is 70 m. After how many seconds from the instant of throwing will the ball reach the ground (a) 2.33 sec        (b) 5.33 sec        (c) 6.33 sec        (d) 9.33 sec Solution: (c) Formula for calculation of time to reach the body on the ground from the tower of height ?h? (If it is thrown vertically up with velocity u) is given by \[t=\frac{u}{g}\left[ 1+\sqrt{1+\frac{2gh}{{{u}^{2}}}} \right]\]             So we can resolve the given velocity in vertical direction and can apply the above formula. Initial vertical component of velocity \[u\sin \theta =50\,\sin 30=25\,m/s.\] \[\therefore \,\,\,t=\frac{25}{9.8}\left[ 1+\sqrt{1+\frac{2\times 9.8\times 70}{{{(25)}^{2}}}} \right]=\text{ }6.33\text{ }sec.\] Problem 25. If for a given angle of projection, the horizontal range is doubled, the time of flight becomes (a) 4 times         (b) 2 times         (c) \[\sqrt{2}\] times        (d) \[1/\sqrt{2}\] times Solution: (c) \[R=\frac{{{u}^{2}}\sin 2\theta }{g}\] and \[T=\frac{2u\sin \theta }{g}\] \[\therefore \,\,\,R\propto {{u}^{2}}\] and \[T\propto u\] (If \[\theta \] and g are constant). In the given condition to make range double, velocity must be increased upto \[\sqrt{2}\] times that of previous value. So automatically time of flight will becomes \[\sqrt{2}\] times. Problem 26. A particle is thrown with velocity u at an angle a from the horizontal. Another particle is thrown with the same velocity at an angle a from the vertical. The ratio of times of flight of two particles will be (a) \[tan\,2\,\alpha :1\]                 (b) \[cot\text{ }2\,\alpha :1\]                    (c) \[tan\,\alpha :\text{ }1\]          (d) \[cot\,\alpha :\text{ }1\] Solution: (c) For first particles angle of projection from the horizontal is a. So \[\,\,{{T}_{1}}=\frac{2u\sin \alpha }{g}\] For second particle angle of projection from the vertical is a. it mean from the horizontal is \[(90-\alpha ).\] \[\therefore \,\,\,\,\,\,{{T}_{2}}=\frac{2u\sin \,(90-\alpha )}{g}=\frac{2u\cos \alpha }{g}\]. So ratio of time of flight \[\frac{{{T}_{1}}}{{{T}_{2}}}=\tan \alpha \]. Problem 27.     The friction of the air causes vertical retardation equal to one tenth of the acceleration due to gravity\[\left( Take g = 10 m{{s}^{2}} \right)\]. The time of flight will be decreased by (a) 0%               (b) 1%               (c) 9%               (d) 11% Solution: (c) \[T=\frac{2u\sin \theta }{g}\] \[\therefore \,\,\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{{{g}_{2}}}{{{g}_{1}}}=\frac{g+\frac{g}{10}}{g}=\frac{11}{10}\] Fractional decrease in time of flight \[=\frac{{{T}_{1}}-{{T}_{2}}}{{{T}_{1}}}=\frac{1}{11}\] \[\operatorname{Percentage} decrease = 9%\]%