NEET Physics Two Dimensional Motion Projectile Motion

Projectile Motion

A hunter aims his gun and fires a bullet directly towards a monkey sitting on a distant tree. If the monkey remains in his position, he will be safe but at the instant the bullet leaves the barrel of gun, if the monkey drops from the tree, the bullet will hit the monkey because the bullet will not follow the linear path.

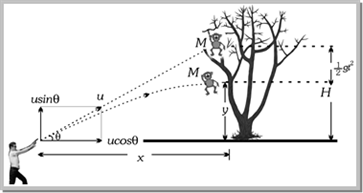
The path of motion of a bullet will be parabolic and this motion of bullet is defined as projectile motion. If the force acting on a particle is oblique with initial velocity then the motion of particle is called projectile motion.  Projectile. A body which is in flight through the atmosphere but is not being propelled by any fuel is called projectile. Example: (i) A bomb released from an aeroplane in level flight             (ii) A bullet fired from a gun             (iii) An arrow released from bow             (iv) A Javelin thrown by an athlete   Assumptions of Projectile Motion. (1) There is no resistance due to air. (2) The effect due to curvature of earth is negligible. (3) The effect due to rotation of earth is negligible. (4) For all points of the trajectory, the acceleration due to gravity ?g? is constant in magnitude and direction.  Principles of Physical Independence of Motions. (1) The motion of a projectile is a two-dimensional motion. So, it can be discussed in two parts. Horizontal motion and vertical motion. These two motions take place independent of each other. This is called the principle of physical independence of motions. (2) The velocity of the particle can be resolved into two mutually perpendicular components. Horizontal component and vertical component. (3) The horizontal component remains unchanged throughout the flight. The force of gravity continuously affects the vertical component. (4) The horizontal motion is a uniform motion and the vertical motion is a uniformly accelerated retarded motion.  Types of Projectile Motion. (1) Oblique projectile motion       (2) Horizontal projectile motion      (3) Projectile motion on an inclined plane

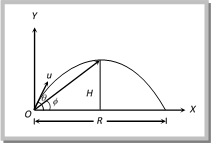
Oblique Projectile. In projectile motion, horizontal component of velocity (u cosq), acceleration (g) and mechanical energy remains constant while, speed, velocity, vertical component of velocity (u sin q), momentum, kinetic energy and potential energy all changes. Velocity, and KE are maximum at the point of projection while minimum (but not zero) at highest point. (1) Equation of trajectory: A projectile thrown with velocity u at an angle q with the horizontal. The velocity u can be resolved into two rectangular components.

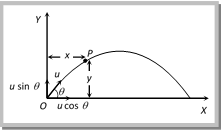
v cos \[\theta \] component along X?axis and u sin q component  along Y?axis. For horizontal motion    \[x=u\text{ }cos\,\,\theta \times t\Rightarrow t=\frac{x}{u\cos \,\theta }\]       ?. (i) For vertical motion          \[y=(u\sin \,\theta \,)\,t-\frac{1}{2}\,g{{t}^{2}}\]                        ?. (ii) From equation (i) and (ii)  \[y=u\sin \theta \left( \frac{x}{u\cos \,\theta } \right)\,-\frac{1}{2}g\,\left( \frac{{{x}^{2}}}{{{u}^{2}}{{\cos }^{2}}\,\theta } \right)\]                         \[y=x\,\tan \,\theta \,-\frac{1}{2}\frac{g{{x}^{2}}}{{{u}^{2}}{{\cos }^{2}}\,\theta }\] This equation shows that the trajectory of projectile is parabolic because it is similar to equation of parabola                         \[\operatorname{y} = ax  b{{x}^{2}}\] Note: Equation of oblique projectile also can be written as                         \[y=x\tan \theta \,\left[ 1-\frac{x}{R} \right]\]                    (where R = horizontal range = \[\frac{{{u}^{2}}\sin 2\theta }{g}\]) Sample problems based on trajectory Problem 1. The trajectory of a projectile is represented by \[y=\sqrt{3}x-g{{x}^{2}}/2\]. The angle of projection is (a) \[{{30}^{o}}\]                    (b) \[{{45}^{o}}\]        (c) \[{{60}^{o}}\]                     (d) None of these Solution: (c) By comparing the coefficient of x in given equation with standard equation \[y=x\tan \theta -\frac{g{{x}^{2}}}{2{{u}^{2}}{{\cos }^{2}}\theta }\] \[\tan \theta =\sqrt{3}\] \[\therefore \,\,\theta =60{}^\circ \] Problem 2. The path followed by a body projected along y-axis is given as by \[y=\sqrt{3}x-(1/2){{x}^{2}}\], if g = 10 m/s, then the initial velocity of projectile will be ? (x and y are in m) (a) \[3\sqrt{10}\,\,m/s\]                (b) \[2\sqrt{10}\,m/s\]                  (c) \[10\sqrt{3}\,m/s\]                  (d) \[10\sqrt{2}\,m/s\] Solution: (b) By comparing the coefficient of x2 in given equation with standard equation \[y=x\tan \theta -\frac{g{{x}^{2}}}{2{{u}^{2}}{{\cos }^{2}}\theta }.\]  \[\frac{g}{2{{u}^{2}}{{\cos }^{2}}\theta }=\frac{1}{2}\] Substituting \[\theta \,\,=\,\,{{60}^{o}}\] we get \[u=2\sqrt{10}\,m/\sec \]. Problem 3. The equation of projectile is \[y=16x-\frac{5{{x}^{2}}}{4}\]. The horizontal range is (a) 16 m            (b) 8 m              (c) 3.2 m           (d) 12.8 m Solution: (d) Standard equation of projectile motion \[y=x\tan \theta \left[ 1-\frac{x}{R} \right]\] Given equation: \[y=16x-\frac{5{{x}^{2}}}{4}\] or \[y=16x\left[ 1-\frac{x}{64/5} \right]\] By comparing above equations \[R=\frac{64}{5}~=12.8\text{ }m.\] Displacement of projectile \[(\vec{r})\]: Let the particle acquires a position P having the coordinates (x, y) just after time t from the instant of projection. The corresponding position vector of the particle at time t is \[\vec{r}\] as shown in the figure.

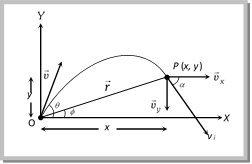
\[\,\,\vec{r}=x\hat{i}+y\hat{j}\]                         ?. (i) The horizontal distance covered during time t is given as \[x={{v}_{x}}\,t\Rightarrow x=u\cos \theta \,\,t\] ?. (ii) The vertical velocity of the particle at time t is given as \[{{v}_{y}}={{({{v}_{0}})}_{y}}-gt,\]             ?. (iii) Now the vertical displacement y is given as \[y=u\sin \theta \,t-1/2\,g{{t}^{2}}\]                   ?. (iv) Putting the values of x and y from equation (ii) and equation (iv) in equation (i) we obtain the position vector at any time t as \[\vec{r}=(u\cos \theta )\,t\,\hat{i}+\left( (u\sin \theta )\,t-\frac{1}{2}g{{t}^{2}} \right)\,\hat{j}\]   \[\Rightarrow \] \[r=\sqrt{{{(u\,t\cos \theta )}^{2}}+{{\left( (u\,t\sin \theta )-\frac{1}{2}g{{t}^{2}} \right)}^{2}}}\] \[r=u\,t\sqrt{1+{{\left( \frac{gt}{2u} \right)}^{2}}-\frac{gt\sin \theta }{u}}\] and \[\varphi ={{\tan }^{-1}}(y/x)\] \[={{\tan }^{-1}}\left( \frac{ut\sin \theta -1/2g{{t}^{2}}}{(u\,t\cos \theta )} \right)\] or \[\varphi ={{\tan }^{-1}}\left( \frac{2u\,\sin \theta -gt}{2u\,\cos \theta } \right)\] Note: q The angle of elevation f of the highest point of the projectile and the angle of projection q are related to each other as

\[\tan \varphi =\frac{1}{2}\tan \theta \]    Sample problems based on displacement Problem 4. A body of mass 2 kg has an initial velocity of 3 m/s along OE and it is subjected to a force of 4 Newton?s in OF direction perpendicular to OE. The distance of the body from O after 4 seconds will be (a) 12 m            (b) 28 m            (c) 20 m             (d) 48 m

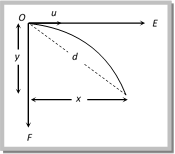
Solution : (c) Body moves horizontally with constant initial velocity 3 m/s upto 4 seconds \[\therefore \,\,\,\,x=ut\,\,=3\times 4=12\,m\]and in perpendicular direction it moves under the effect of constant force with zero initial velocity upto 4 seconds. \[\therefore \,\,\,\,\,y=ut+\frac{1}{2}(a)\,{{t}^{2}}=0+\frac{1}{2}\left( \frac{F}{m} \right)\,{{t}^{2}}=\frac{1}{2}\left( \frac{4}{2} \right)\,{{4}^{2}}=16\,m\] So its distance from O is given by \[d=\sqrt{{{x}^{2}}+{{y}^{2}}}\,\,\,=\sqrt{{{(12)}^{2}}+{{(16)}^{2}}}\] \[\therefore \,\,\,\,\,\,\,\,\,\,d=20\,m\] Problem 5. A body starts from the origin with an acceleration of 6 m/s2 along the x-axis and 8 m/s2 along the y-axis. Its distance from the origin after 4 seconds will be [MP PMT 1999] (a) 56 m            (b) 64 m            (c) 80 m            (d) 128 m Solution: (c) Displacement along X- axis: \[x={{u}_{x}}t+\frac{1}{2}{{a}_{x}}{{t}^{2}}\]\[=\frac{1}{2}\times 6\times {{(4)}^{2}}=48\,m\] Displacement along Y- axis: \[y={{u}_{y}}t+\frac{1}{2}{{a}_{y}}{{t}^{2}}=\frac{1}{2}\times 8\times {{(4)}^{2}}=64\,m\] Total distance from the origin \[=\sqrt{{{x}^{2}}+{{y}^{2}}}=\sqrt{{{(48)}^{2}}+{{(64)}^{2}}}=80\,m\] (3) Instantaneous velocity v: In projectile motion, vertical component of velocity changes but horizontal component of velocity remains always constant. Example: When a man jumps over the hurdle leaving behind its skateboard then vertical component of his velocity is changing, but not the horizontal component, which matches with the skateboard velocity. As a result, the skateboard stays underneath him, allowing him to land on it.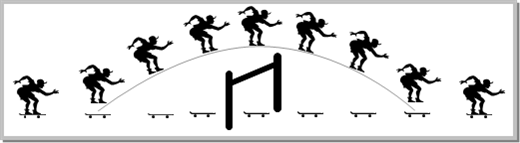

Let \[{{v}_{i}}\] be the instantaneous velocity of projectile at time t direction of this velocity is along the tangent to the trajectory at point P. \[{{\vec{v}}_{i}}={{v}_{x}}i+{{v}_{y}}\hat{j}\Rightarrow {{v}_{i}}=\sqrt{v_{x}^{2}+v_{y}^{2}}\]\[=\sqrt{{{u}^{2}}{{\cos }^{2}}\,\theta +{{(u\sin \theta -gt)}^{2}}}\]  \[{{v}_{i}}=\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}-2u\,gt\sin \theta }\]      Direction of instantaneous velocity \[\tan \alpha \,=\,\frac{{{v}_{y}}}{{{v}_{x}}}=\frac{u\,\sin \,\theta -gt}{u\,\cos \theta }\]  or       \[\alpha ={{\tan }^{-1}}\left[ \tan \theta -\frac{gt}{u}\sec \theta  \right]\] (4) Change in velocity: Initial velocity (at projection point) \[{{\overrightarrow{u}}_{i}}=u\cos \theta \,\hat{i}+u\sin \theta \,\hat{j}\] Final velocity (at highest point) \[{{\overrightarrow{u}}_{f}}=u\cos \theta \,\hat{i}+0\,\hat{j}\] (i) Change in velocity (Between projection point and highest point) \[\Delta u={{\overrightarrow{u}}_{f}}-{{\overrightarrow{u}}_{i}}=-u\sin \theta \,\hat{j}\] When body reaches the ground after completing its motion then final velocity \[{{\overrightarrow{u}}_{f}}=u\cos \theta \,\hat{i}-u\sin \theta \,\hat{j}\] (ii) Change in velocity (Between complete projectile motion) \[\Delta u={{u}_{f}}-{{u}_{i}}=-2u\sin \theta \,\hat{i}\] Sample problems based on velocity Problem 6. In a projectile motion, velocity at maximum height is [AIEEE 2002] (a) \[\frac{u\,\cos \,\theta }{2}\]               (b) \[u\,\cos \,\theta \]      (c) \[\frac{u\,\sin \,\theta }{2}\]                (d) None of these Solution: (b) In a projectile motion at maximum height body possess only horizontal component of velocity i.e. u cosq. Problem 7. A body is thrown at angle \[{{30}^{o}}\] to the horizontal with the velocity of 30 m/s. After 1 sec, its velocity will be (in m/s) \[\left( g= 10m/{{s}^{2}} \right)\] (a) \[10\sqrt{7}\] (b) \[700\sqrt{10}\]                     (c) \[100\sqrt{7}\]                       (d) \[\sqrt{40}\] Solution: (a) From the formula of instantaneous velocity \[v=\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}-2\,u\,g\,t\,\sin \theta }\] \[v=\sqrt{{{(30)}^{2}}+{{(10)}^{2}}\times {{1}^{2}}-2\times 30\times 10\times 1\times \sin {{30}^{o}}}\] \[=10\sqrt{7}\,m/s\] Problem 8. A projectile is fired at \[{{30}^{o}}\] to the horizontal. The vertical component of its velocity is 80 ms?1. Its time of flight is T. What will be the velocity of the projectile at \[\operatorname{t} = T/2\] (a) \[80\text{ }m{{s}^{1}}\]      (b) \[80\sqrt{3}\,m{{s}^{1}}\]               (c) \[(80/\sqrt{3})\,m{{s}^{-1}}\]            (d) \[40 m{{s}^{1}}\] Solution: (b) At half of the time of flight, the position of the projectile will be at the highest point of the parabola and at that position particle possess horizontal component of velocity only. Given \[{{u}_{vertical}}=u\sin \theta =80\Rightarrow u=\frac{80}{\sin {{30}^{o}}}=160\,m/s\] \[\therefore \,\,\,\,\,\,\,{{u}_{horizontal}}=u\cos \theta =160\,\,\cos {{30}^{o}}=80\sqrt{3}\,m/s.\] Problem 9. A particle is projected from point O with velocity u in a direction making an angle \[\alpha \] with the horizontal. At any instant its position is at point P at right angles to the initial direction of projection. Its velocity at point P is             

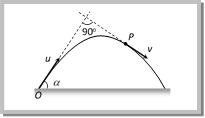
          (a) \[u\text{ }tan\,\alpha \]                                   (b) \[u\text{ }cot\,\alpha \] (c) \[u\,\cos ec\,\,\alpha \]                         (d) \[u\text{ }sec\,\alpha \] Solution: (b) Horizontal velocity at point \['O'=u\cos \alpha \] Horizontal velocity at point \['P'=v\sin \alpha \] In projectile motion horizontal component of velocity remains constant throughout the motion

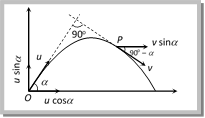
\ \[v\sin \alpha =u\cos \alpha \] Þ \[\,v=u\cot \alpha \] Problem 10. A particle P is projected with velocity u1 at an angle of \[{{30}^{o}}\] with the horizontal. Another particle Q is thrown vertically upwards with velocity u2 from a point vertically below the highest point of path of P. The necessary condition for the two particles to collide at the highest point is (a) \[{{u}_{1}}={{u}_{2}}\]                             (b) \[{{u}_{1}}=2{{u}_{2}}\] (c) \[{{u}_{1}}=\frac{{{u}_{2}}}{2}\]                          (d) \[{{u}_{1}}=4{{u}_{2}}\] Solution: (b) Both particle collide at the highest point it means the vertical distance travelled by both the particle will be equal, i.e. the vertical component of velocity of both particle will be equal \[{{u}_{1}}\,\sin 30{}^\circ ={{u}_{2}}\Rightarrow \frac{{{u}_{1}}}{2}={{u}_{2}}\,\,\,\,\,\,\,\therefore \,\,\,\,{{u}_{1}}=2{{u}_{2}}\] Problem 11. Two seconds after projection a projectile is travelling in a direction inclined at \[{{30}^{o}}\] to the horizontal after one more sec, it is travelling horizontally, the magnitude and direction of its velocity are [RPET 1999]

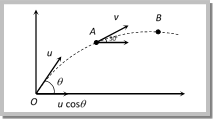
(a) \[2\sqrt{20}\,m/\sec ,\,{{60}^{o}}\]   (b) \[20\sqrt{3}\,m/\sec ,\,\,{{60}^{o}}\] (c) \[6\sqrt{40}\,\,m/\sec ,\,\,{{30}^{o}}\]          (d) \[40\sqrt{6}\,m/\sec ,\,\,{{30}^{o}}\] Solution: (b) Let in 2 sec body reaches upto point A and after one more sec upto point B. Total time of ascent for a body is given 3 sec i.e.  \[t=\frac{u\sin \theta }{g}=3\] \[\therefore \,\,u\sin \theta =10\times 3=30\]                      ?.. (i) Horizontal component of velocity remains always constant \[u\cos \theta =v\cos 30{}^\circ \]                       ?.. (ii) For vertical upward motion between point O and A \[v\sin {{30}^{o}}=u\sin \theta -g\times 2\]         \[\left[ \text{Using }v=u-g\,t \right]\] \[v\sin {{30}^{o}}=30-20\]                   \[\left[ \text{As}\,\,u\sin \text{ }\theta =\text{30} \right]\] \[\therefore \,\,v=20\,m/s.\] Substituting this value in equation (ii)         \[u\cos \theta =20\,\cos {{30}^{o}}\]\[=10\sqrt{3}\] ?..(iii) From equation (i) and (iii) \[u=20\sqrt{3}\] and \[\theta =60{}^\circ \] Problem 12. A body is projected up a smooth inclined plane (length = \[20\sqrt{2}\,m\]) with velocity u from the point M as shown in the figure. The angle of inclination is 45o and the top is connected to a well of diameter 40 m. If the body just manages to cross the well, what is the value of v.

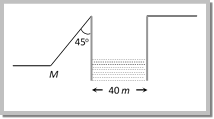
(a) \[40\,m{{s}^{-1}}\]             (b) \[40\sqrt{2}\,m{{s}^{-1}}\] (c) \[20\,m{{s}^{-1}}\]              (d) \[20\sqrt{2}\,m{{s}^{-1}}\] Solution: (d) At point N angle of projection of the body will be \[45{}^\circ \]. Let velocity of projection at this point is v. If the body just manages to cross the well then \[\text{Range}=\text{Diameter}\,\text{of}\,\text{well}\]

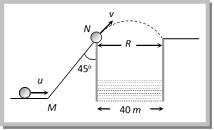
\[\frac{{{v}^{2}}\sin 2\theta }{g}=40\]       \[\left[ \text{As}\,\,\theta =\text{45}{}^\circ  \right]\] \[{{v}^{2}}=400\,\,\,\,\,\,\,\,\,\Rightarrow \,\,\,\,\,\,\,v=20\,m/s\] But we have to calculate the velocity (u) of the body at point M. For motion along the inclined plane (from M to N) Final velocity \[\left( v \right) = 20 m/s,\] acceleration (a) \[=  g sina=  g sin 4{{5}^{o}}\], distance of inclined plane \[\left( s \right)=20\sqrt{2}\,m\] \[{{(20)}^{2}}={{u}^{2}}-2\frac{g}{\sqrt{2}}.20\sqrt{2}\]        \[\left[ Using {{v}^{2}}= {{u}^{2}}+ 2as \right]\] \[{{u}^{2}}={{20}^{2}}+400\Rightarrow u=20\sqrt{2}\,m/s\] Problem 13. A projectile is fired with velocity u making angle q with the horizontal. What is the change in velocity when it is at the highest point (a) \[u\text{ }cos\,\theta \]           (b) u                  (c) \[u\text{ }sin\,\theta \] (d) \[(u\text{ }cos\,\theta u)\] Solution: (c) Since horizontal component of velocity remain always constant therefore only vertical component of velocity changes. Initially vertical component \[u\sin \theta \] Finally it becomes zero. So change in velocity \[=u\sin \theta \]