Interference of Sound Waves
Category : JEE Main & Advanced
(1) When two waves of same frequency, same wavelength, same velocity (nearly equal amplitude) moves in the same direction, Their superimposition results in the interference.
(2) Due to interference the resultant intensity of sound at that point is different from the sum of intensities due to each wave separately.
(3) Interference is of two type (i) Constructive interference (ii) Destructive interference.
(4) In interference energy is neither created nor destroyed but is redistributed.
(5) For observable interference, the sources (producing interfering waves) must be coherent.
(6) Let at a given point two waves arrives with phase difference \[\phi \] and the equation of these waves is given by
\[{{y}_{1}}={{a}_{1}}\sin \omega t,\,\,{{y}_{2}}={{a}_{2}}\sin \,\,(\omega t+\phi )\,\] then by the principle of superposition \[\vec{y}\,=\,{{\vec{y}}_{1}}\,+\,{{\vec{y}}_{2}}\]
\[\Rightarrow \] \[y={{a}_{1}}\sin \omega t+{{a}_{2}}\sin \,(\omega t+\phi )=A\,\,\sin \,(\omega t+\theta )\]
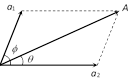
where \[A\,=\,\sqrt{{{a}_{1}}^{2}\,+\,{{a}_{2}}^{2}\,+\,2{{a}_{1}}{{a}_{2}}\,\cos \,\varphi }\]
and tan \[\theta =\frac{{{a}_{2}}\sin \,\varphi }{{{a}_{1}}\,+\,a{}_{2}\cos \,\,\varphi }\]
since Intensity \[(l)\propto \] (Amplitude A)\[^{2}\]\[\Rightarrow \]\[\frac{{{I}_{1}}}{{{I}_{2}}}={{\left( \frac{{{a}_{1}}}{{{a}_{2}}} \right)}^{2}}\]
Therefore, the resultant intensity is given by
\[I=\,{{I}_{1}}\,+\,{{I}_{2}}\,+\,2\,\sqrt{{{I}_{1}}{{I}_{2}}}\,\cos \,\varphi \]
Constructive and destructive interference
| Constructive interference | Destructive interference |
| When the waves meets a point with same phase, constructive interference is obtained at that point (i.e. maximum sound). | When the wave meets a point with opposite phase, destructive interference is obtained at that point (i.e. minimum sound) |
| Phase difference between the waves at the point of observation \[\phi ={{0}^{o}}\] or \[2n\pi \] | Phase difference \[\phi ={{180}^{o}}\] or \[(2n-1)\,\pi \,;\,\] n = 1, 2, ... |
| Path difference between the waves at the point of observation \[\Delta =n\lambda \](i.e. even multiple of \[\lambda /2\]) | Path difference \[\Delta =(2n-1)\frac{\lambda }{2}\] (i.e. odd multiple of \[\lambda /2\]) |
| Resultant amplitude at the point of observation will be maximum \[{{A}_{\max }}={{a}_{1}}+{{a}_{2}}\] If \[{{a}_{1}}={{a}_{2}}={{a}_{0}}\Rightarrow {{A}_{\max }}=2{{a}_{0}}\] | Resultant amplitude at the point of observation will be minimum \[{{A}_{\min }}={{a}_{1}}-{{a}_{2}}\] If \[{{a}_{1}}={{a}_{2}}\Rightarrow {{A}_{\min }}=0\] |
| Resultant intensity at the point of observation will be maximum \[{{I}_{\max }}={{I}_{1}}+{{I}_{2}}+2\sqrt{{{I}_{1}}{{I}_{2}}}\]\[={{\left( \sqrt{{{I}_{1}}}+\sqrt{{{I}_{2}}} \right)}^{2}}\] If \[{{I}_{1}}={{I}_{2}}={{I}_{0}}\Rightarrow {{I}_{\max }}=4{{I}_{0}}\] | Resultant intensity at the point of observation will be minimum \[{{I}_{\min }}={{I}_{1}}+{{I}_{2}}-2\sqrt{{{I}_{1}}{{I}_{2}}}\]\[={{\left( \sqrt{{{I}_{1}}}-\sqrt{{{I}_{2}}} \right)}^{2}}\] If \[{{I}_{1}}={{I}_{2}}={{I}_{0}}\Rightarrow {{I}_{\min }}=0\] |
(7) \[\frac{{{I}_{\max }}}{{{I}_{\min }}}={{\left( \frac{\sqrt{{{I}_{1}}}+\sqrt{{{I}_{2}}}}{\sqrt{{{I}_{1}}}-\sqrt{{{I}_{2}}}} \right)}^{2}}={{\left( \frac{\sqrt{\frac{{{I}_{1}}}{{{I}_{2}}}}+1}{\sqrt{\frac{{{I}_{1}}}{{{I}_{2}}}}-1} \right)}^{2}}\]\[={{\left( \frac{{{a}_{1}}+{{a}_{2}}}{{{a}_{1}}-{{a}_{2}}} \right)}^{2}}={{\left( \frac{\frac{{{a}_{1}}}{{{a}_{2}}}+1}{\frac{{{a}_{1}}}{{{a}_{2}}}-1} \right)}^{2}}\]
You need to login to perform this action.
You will be redirected in
3 sec
