JEE Main & Advanced Physics Semiconducting Devices Terms Related with Crystal Structure

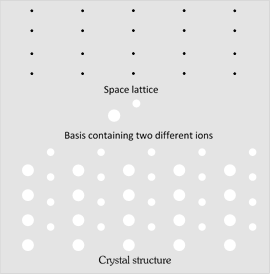
(1) Crystal lattice : It is a geometrical arrangement of points in space where if atoms or molecules of a solid are placed, we obtain an actual crystal structure of the solid.

(2) Basis : The atoms or molecules attached with every lattice point in a crystal structure is called the basis of crystal structure.

(3) Unit cell : Is defined as that volume of the solid from which the entire crystal structure can be constructed by the translational repetition in three dimensions. The length of three sides of a unit cell (3D) are called primitives or lattice constant they are denoted by a, b, c

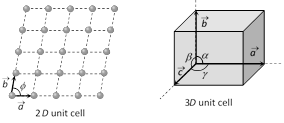
(4) Primitive cell : A primitive cell is a minimum volume unit cell or the simple unit cell with particles only at the corners is a primitive unit cell and other types of unit cells are called non-primitive unit cells. There is only one lattice point per primitive cell.

(5) Crystallographic axis : The lines drawn parallel to the lines of intersection of the faces of the unit cell are called crystallographic axis. All the crystals on the basis of the shape of their unit cells, have been divided into seven crystal systems as shown in the following table.      

Different crystal systems

System	Lattice constants	Angle between lattice constants	Examples
Cubic 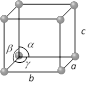          Number of lattices = 3	\[a=b=c\]	\[\alpha =\beta =\gamma ={{90}^{o}}\]	Diamond, NaCl, Li, Ag, Cu, \[N{{H}_{4}}Cl\], Pb etc.

Tetragonal Number of lattices = 2	\[a=b\ne c\]	\[\alpha =\beta ={{90}^{o}}\]	White tin, \[NiS{{O}_{4}}\] etc.
Orthorhombic 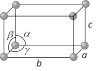Number of lattices = 4	\[a\ne b\ne c\]	\[\alpha =\beta =\gamma ={{90}^{o}}\]	\[HgC{{l}_{2}},\,KN{{O}_{3}}\], gallium etc.
Monoclinic 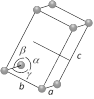Number of lattices = 2	\[a=b\ne c\]	\[\alpha =\gamma ={{90}^{o}}\] and \[\beta \ne {{90}^{o}}\]	\[Kcl{{O}_{3}},\,FeS{{O}_{4}}\] etc.
Triclinic 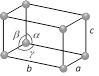Number of lattices = 1	\[a\ne b\ne c\]	\[\alpha \ne \beta \ne \gamma \ne {{90}^{o}}\]	\[{{K}_{2}}C{{r}_{2}}{{O}_{7}},\,CuS{{O}_{4}}\]  etc.
Rhombo-hedral or Trigonal 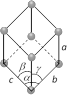Number of lattices = 1	\[a=b=c\]	\[\alpha =\beta =\gamma \ne {{90}^{o}}\]	Calcite, As, Sb, Bi etc.
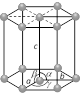Hexagonal             Number of lattices = 1	\[a=b\ne c\]	\[\alpha =\beta ={{90}^{o}}\] and \[\gamma ={{120}^{o}}\]	Zn, Cd, Ni etc.