JEE Main & Advanced Physics Semiconducting Devices Boolean Algebra

(1) In Boolean algebra only two states of variables (0 and 1) are allowed.

(2) The variables (A, B, C ....) of Boolean Algebra are subjected to three operations.

(i) OR Operation : Represented by (+) sign

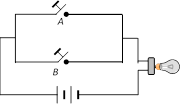
Boolean expression  \[Y=A+B\]

When switch A or B is closed ? Bulb glows

(ii) AND Operation : Represented by \[(.)\] sign

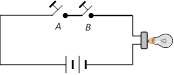
Boolean expression \[Y=A\cdot B\]

When switches A and B both are closed ? Bulb glows

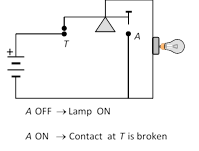
(iii) NOT Operation : Represented by bar over the variables

Boolean expression  \[Y=\bar{A}\]

(3) Basic Boolean postulates and laws

(i) Boolean Postulates : \[0+A=A,\]          \[1\,\,\cdot \text{ }A=A,\]                                        

\[1+A=1,\]         

\[0\cdot A=0,\]                                        

\[A+\bar{A}=1\]

(ii) Identity law :               \[A+A=A,\]         \[A\cdot A=A\]

(iii) Negation law :            \[\overline{{\bar{A}}}=A\]

(iv) Commutative law : \[A+B=B+A,\]    \[A\cdot B=B\cdot A\]

(v) Associative law :        \[(A+B)+C=A+(B+C),\]                                        

\[(A\cdot B)\cdot C=A\cdot (B\cdot C)\]

(vi) Distributive law :       \[A\cdot (B+C)=A\cdot B+A\cdot C\]                                        

\[(A+B)\cdot (A+C)=A+BC\]

(vii) Absorption laws :    \[A+A\cdot B=A,\]          \[A\cdot (A+B)=A\]                                        

\[\overline{A}\,\text{ }\!\!\cdot\!\!\text{ }\,(A+B\text{)}=\overline{A}\,\text{ }\!\!\cdot\!\!\text{ }\,B\]

(viii) Boolean identities :   \[A+\overline{A}\,B=A+B\], \[A(\overline{A}+B)=AB\],

\[A+BC=(A+B)\,(A+C)\], \[(\overline{A}+B)\,\text{ }\!\!\cdot\!\!\text{ }\,\text{(}A+C)\,=\overline{A}C+AB\]

(ix) De Morgan's theorem : It states that the complement of the whole sum is equal to the product of individual complements and vice versa i.e.

\[\overline{A+B}=\bar{A}\cdot \bar{B}\] and \[\overline{A\cdot B}=\bar{A}+\bar{B}\]