Heisenberg Uncertainty Principle
Category : JEE Main & Advanced
(1) According to Heisenberg's uncertainty principle, it is impossible to measure simultaneously both the position and the momentum of the particle.
(2) Let \[\Delta x\] and \[\Delta p\] be the uncertainty in the simultaneous measurement of the position and momentum of the particle, then \[\Delta x\Delta p=\hbar \]; where \[\hbar =\frac{h}{2\pi }\] and \[h=6.63\times {{10}^{-34}}\,J-s\] is the Planck's constant. \[(\frac{h}{2\pi }=1.05\times {{10}^{-34}}J\text{-}sec\text{)}\]
A more rigorous treatment gives \[\Delta x..\Delta p\ge \frac{\hbar }{2}\,\,\left( \text{or}\,\frac{\text{h}}{\text{4}\pi } \right)\].
(3) If \[\Delta x=0\] then \[\Delta p=\infty \] and if \[\Delta p=0\] then \[\Delta x=\infty \]
i.e., if we are able to measure the exact position of the particle (say an electron) then the uncertainty in the measurement of the linear momentum of the particle is infinite. Similarly, if we are able to measure the exact linear momentum of the particle i.e., \[\Delta p=0\], then we can not measure the exact position of the particle at that time.
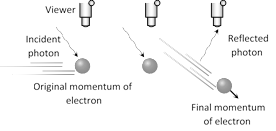
An electron cannot be observed without changing it's momentum
(4) Uncertainty principle successfully explains
(i) Non-existence of electrons in the nucleus
(ii) Finite size of spectral lines.
(5) The Heisenberg uncertainty principle is also applicable to energy and time, angular momentum and angular displacement. Hence \[\Delta E.\,\Delta t\ge \frac{h}{2\pi }\] and \[\Delta L.\,\Delta \theta \ge \frac{h}{2\pi }\]
(6) If the radius of the nucleus is r then the probability of finding the electron inside the nucleus is \[\Delta x=2r\] and uncertainty in momentum is \[\Delta p=\frac{h}{4\pi r}\]
You need to login to perform this action.
You will be redirected in
3 sec
