Motion of Block Motion of Blocks in Contact.
| Condition | Free body diagram | Equation | Force and acceleration |
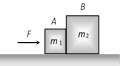 |  | \[F-f={{m}_{1}}a\]. | \[a=\frac{F}{{{m}_{1}}+{{m}_{2}}}\] |
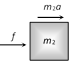 | \[f={{m}_{2}}a\] | \[f=\frac{{{m}_{2}}F}{{{m}_{1}}+{{m}_{2}}}\]. |
 |   | \[f={{m}_{1}}a\] | \[a=\frac{F}{{{m}_{1}}+{{m}_{2}}}\] |
| | \[F-f={{m}_{2}}a\]. | \[f=\frac{{{m}_{1}}F}{{{m}_{1}}+{{m}_{2}}}\]. |
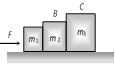 |    | \[F-{{f}_{1}}={{m}_{1}}a\] | \[a=\frac{F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\] |
| | 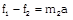 | \[{{f}_{1}}=\frac{({{m}_{2}}+{{m}_{3}})F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]. |
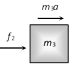
| | \[{{f}_{2}}={{m}_{3}}a\]. | \[{{f}_{2}}=\frac{{{m}_{3}}F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]. |
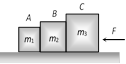 | 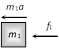  | \[{{f}_{1}}={{m}_{1}}a\]. | \[a=\frac{F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]. |
 | 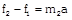 | \[{{f}_{1}}=\frac{{{m}_{1}}F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]. |
| | 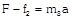 | \[{{f}_{2}}=\frac{({{m}_{1}}+{{m}_{2}})F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]. |
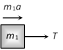
Sample problems based on motion of blocks in contact Problem 43. Two blocks of mass 4 kg and 6 kg are placed in contact with each other on a frictionless horizontal surface. If we apply a push of 5 N on the heavier mass, the force on the lighter mass will be
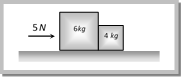
(a) 5 N (b) 4 N (c) 2 N (d) None of the above Solution: (c) Let \[{{m}_{1}}=6kg,\,{{m}_{2}}=4kg\] and \[F=5N\] (given) Force on the lighter mass = \[\frac{{{m}_{2}}\times F}{{{m}_{1}}+{{m}_{2}}}\]\[=\frac{4\times 5}{6+4}\]\[=2N\] Problem 44. In the above problem, if a push of 5 N is applied on the lighter mass, the force exerted by the lighter mass on the heavier mass will be (a) 5 N (b) 4 N (c) 2 N (d) None of the above Solution: (d) Force on the heavier mass \[=\frac{{{m}_{1}}F}{{{m}_{1}}+{{m}_{2}}}\]\[=\frac{6\times 5}{6+4}\] \[=3N\] Problem 45. In the above problem, the acceleration of the lighter mass will be (a) \[0.5\,m{{s}^{-2}}\] (b) \[\frac{5}{4}\,\,m{{s}^{-2}}\] (c) \[\frac{5}{6}\,\,m{{s}^{-2}}\] (d) None of the above Solution: (a) \[\text{Acceleration}=\frac{\text{Net force on the system}}{\text{Total mass of the system}}\]\[=\frac{5}{10}=0.5\,m/{{s}^{2}}\] Problem 46. Two blocks are in contact on a frictionless table one has a mass m and the other 2 m as shown in figure. Force F is applied on mass 2m then system moves towards right. Now the same force F is applied on m. The ratio of force of contact between the two blocks will be in the two cases respectively.
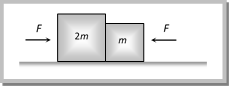
(a) 1 : 1 (b) 1 : 2 (c) 1 : 3 (d) 1 : 4 Solution: (b) When the force is applied on mass 2m contact force \[{{f}_{1}}=\frac{m}{m+2m}g=\frac{g}{3}\] When the force is applied on mass m contact force \[{{f}_{2}}=\frac{2m}{m+2m}g=\frac{2}{3}g\] Ratio of contact forces \[\frac{{{f}_{1}}}{{{f}_{2}}}=\frac{1}{2}\] Motion of Blocks Connected by Mass Less String.
| Condition | Free body diagram | Equation | Tension and acceleration |
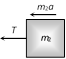
 |  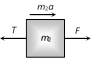 | \[T={{m}_{1}}a\] | \[a=\frac{F}{{{m}_{1}}+{{m}_{2}}}\]. |
| | 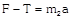 | \[T=\frac{{{m}_{1}}F}{{{m}_{1}}+{{m}_{2}}}\]. |
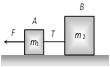 |   | 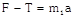 | \[a=\frac{F}{{{m}_{1}}+{{m}_{2}}}\] |
| | 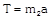 | \[T=\frac{{{m}_{2}}F}{{{m}_{1}}+{{m}_{2}}}\]. |
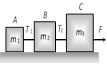 | 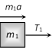 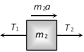 | \[{{T}_{1}}={{m}_{1}}a\] | \[a=\frac{F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]. |
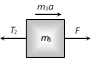 | 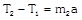 | \[{{T}_{1}}=\frac{{{m}_{1}}F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]. |
| | 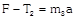 | \[{{T}_{2}}=\frac{({{m}_{1}}+{{m}_{2}})F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]. |
 |  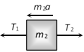 | 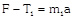 | \[a=\frac{F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\] |
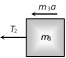 | 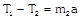 | 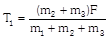 |
| | 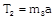 | 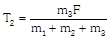 |
Sample problems based on motion of blocks connected by mass less string Problem 47. A monkey of mass 20 kg is holding a vertical rope. The rope will not break when a mass of 25 kg is suspended from it but will break if the mass exceeds 25 kg. What is the maximum acceleration with which the monkey can climb up along the rope \[(g=10m/{{s}^{2}})\] [CBSE 2003] (a) \[10\,m/{{s}^{2}}\] (b) \[25\,m/{{s}^{2}}\] (c) \[2.5m/{{s}^{2}}\] (d) \[5m/{{s}^{2}}\] Solution: (c) Maximum tension that string can bear \[\left( {{T}_{max}} \right) = 25\,\,\times \,\,g N = 250 N\] Tension in rope when the monkey climb up \[T=m\left( g+a \right)\] For limiting condition \[T={{T}_{\max }}\] Þ \[m(g+a)=250\] Þ \[20\,\left( 10+a \right)\,=\,250\] \[\therefore \,\,\,\,\,\,a=2.5\,m/{{s}^{2}}\] Problem 48. Three blocks of masses 2 kg, 3 kg and 5 kg are connected to each other with light string and are then placed on a frictionless surface as shown in the figure. The system is pulled by a force \[F=10N,\] then tension \[{{T}_{1}}=\] [Orissa JEE 2002]
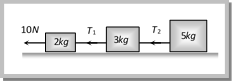
(a) 1 N (b) 5 N (c) 8 N (d) 10 N Solution: (c) By comparing the above problem with general expression. \[{{T}_{1}}=\frac{\left( {{m}_{2}}+{{m}_{3}} \right)F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\] \[=\frac{\left( 3+5 \right)\,10}{2+3+5}\]\[=8\,Newton\] Problem 49. Two blocks are connected by a string as shown in the diagram. The upper block is hung by another string. A force F applied on the upper string produces an acceleration of \[2m/{{s}^{2}}\] in the upward direction in both the blocks. If T and \[{T}'\] be the tensions in the two parts of the string, then [AMU (Engg.) 2000]
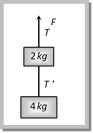
(a) \[T=70.8N\] and \[{T}'=47.2N\] (b) \[T=58.8N\] and \[{T}'=47.2N\] (c) \[T=70.8N\] and \[{T}'=58.8N\] (d) \[T=70.8N\] and \[{T}'=0\]
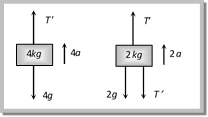
Solution: (a) From F.B.D. of mass 4 kg \[4a=T'-4g\] .?. (i) From F.B.D. of mass 2 kg \[2a=T=T'-2g\] .?. (ii) For total system upward force \[F=T=\left( 2+4 \right)\,\left( g+a \right)\]\[=6\,\left( 18+2 \right)\,N\]= 70.8 N by substituting the value of T in equation (i) and (ii) and solving we get \[T'=47.2N\] Problem 50. Three masses of 15 kg. 10 kg and 5 kg are suspended vertically as shown in the fig. If the string attached to the support breaks and the system falls freely, what will be the tension in the string between 10 kg and 5 kg masses. Take \[g=10\,m{{s}^{-2}}\]. It is assumed that the string remains tight during the motion
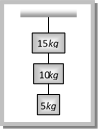
(a) 300 N (b) 250 N (c) 50 N (d) Zero Solution: (d) In the condition of free fall, tension becomes zero. Problem 51. A sphere is accelerated upwards with the help of a cord whose breaking strength is five times its weight. The maximum acceleration with which the sphere can move up without cord breaking is (a) 4g (b) 3g (c) 2g (d) g Solution: (a) Tension in the cord \[= m\left( g + a \right)\] and breaking strength = 5 mg For critical condition \[m\left( g+a \right)\,=\,5mg\,\,\,\,\Rightarrow \,\,\,a=4g\] This is the maximum acceleration with which the sphere can move up with cord breaking.
Motion of Connected Block Over a Pulley
| Condition | Free body diagram | Equation | Tension and acceleration |
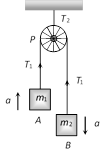 |  | \[{{m}_{1}}a={{T}_{1}}-{{m}_{1}}g\] | \[{{T}_{1}}=\frac{2{{m}_{1}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}g\] |
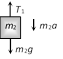 | \[{{m}_{2}}a={{m}_{2}}g-{{T}_{1}}\]. | 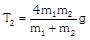 |
| | 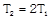 | 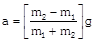 |
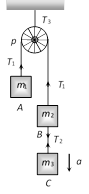 |  | 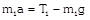 | 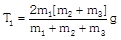 |
 | 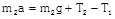 | 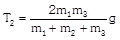 |
 | 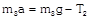 | \[{{T}_{3}}=\frac{4{{m}_{1}}[{{m}_{2}}+{{m}_{3}}]}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}g\]. |
 | 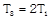 | 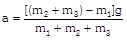 |
| Condition | Free body diagram | Equation | Tension and acceleration |
When pulley have a finite mass M and radius R then tension in two segments of string are different 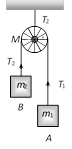 | 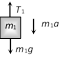 | 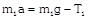 | 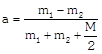 |
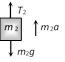 | 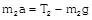 | 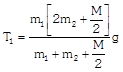 |
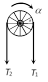 | Torque 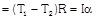 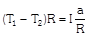 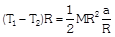 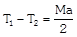 | 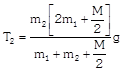 |
 |  | 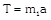 | 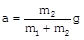 |
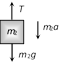 | 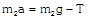 | 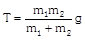 |
 |   | 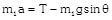 | 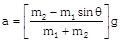 |
| | 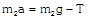 | 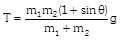 |
 |  |  | 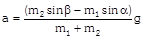 |
 | 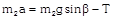 | 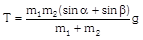 |
| Condition | Free body diagram | Equation | Tension and acceleration |
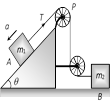 | 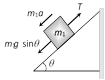 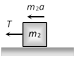 | 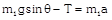 | 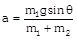 |
| | 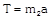 | 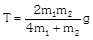 |
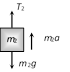
 As As 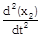 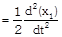  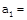 acceleration of block A acceleration of block A 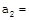 acceleration of block B acceleration of block B | 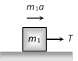 | 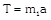 | 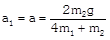 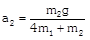 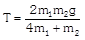 |
 | 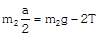 |
 |  | 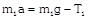 | 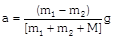 |
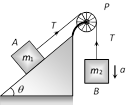
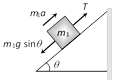
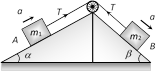
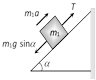
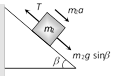
 | 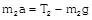 | 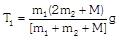 |
 | 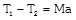 | 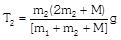 |
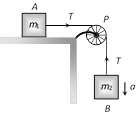
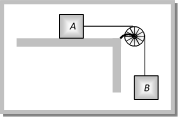
Sample problems based on motion of blocks over pulley Problem 52. A light string passing over a smooth light pulley connects two blocks of masses \[{{m}_{1}}\] and \[{{m}_{2}}\] (vertically). If the acceleration of the system is g/8 then the ratio of the masses is [AIEEE 2002] (a) 8 : 1 (b) 9 : 7 (c) 4 : 3 (d) 5 : 3 Solution: (b) \[a=\left( \frac{{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right)\,g=\frac{g}{8}\]; by solving \[\frac{{{m}_{2}}}{{{m}_{1}}}=9/7\] Problem 53. A block A of mass 7 kg is placed on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 3 kg at the other end. The acceleration of the system is (given g = 10\[m{{s}^{-2}})\] [Kerala (Engg.) 2000]
(a) \[100\,m{{s}^{-2}}\] (b) \[3m{{s}^{-2}}\] (c) \[10m{{s}^{-2}}\] (d) \[30m{{s}^{-2}}\] Solution: (b) \[a=\left( \frac{{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right)\,g\] \[={{\left( \frac{3}{7+3} \right)}^{10}}=3m/{{s}^{2}}\] Problem 54. Two masses \[{{m}_{1}}\] and \[{{m}_{2}}\] are attached to a string which passes over a frictionless smooth pulley. When \[{{m}_{1}}=10\,kg,\] \[{{m}_{2}}=6\,kg,\,\]the acceleration of masses is [Orissa JEE 2002]
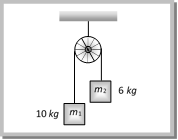
(a) 20\[m/{{s}^{2}}\] (b) \[5m/{{s}^{2}}\] (c) 2.5\[m/{{s}^{2}}\] (d) \[10\,m/{{s}^{2}}\] Solution: (c) \[a=\frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\left( \frac{10-6}{10+6} \right)\,10\]\[=2.5\,m/{{s}^{2}}\] Problem 55. Two weights \[{{W}_{1}}\] and \[{{W}_{2}}\] are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up with an acceleration g, the tension in the string will be (a) \[\frac{4{{W}_{1}}{{W}_{2}}}{{{W}_{1}}+{{W}_{2}}}\] (b) \[\frac{2{{W}_{1}}{{W}_{2}}}{{{W}_{1}}+{{W}_{2}}}\] (c) \[\frac{{{W}_{1}}{{W}_{2}}}{{{W}_{1}}+{{W}_{2}}}\] (d) \[\frac{{{W}_{1}}{{W}_{2}}}{2\,({{W}_{1}}+{{W}_{2}})}\] Solution: (a) When the system is at rest tension in string \[T=\frac{2{{m}_{1}}{{m}_{2}}}{\left( {{m}_{1}}+{{m}_{2}} \right)}g\] If the system moves upward with acceleration g then \[T=\frac{2{{m}_{1}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}\left( g+g \right)\] \[=\frac{4{{m}_{1}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}g\] or \[T=\frac{4{{w}_{1}}{{w}_{2}}}{{{w}_{1}}+{{w}_{2}}}\] Problem 56. Two masses \[{{\operatorname{M}}_{1}}\,\,and {{M}_{2}}\] are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane in \[\theta \]. Take \[\operatorname{g} = 10 m{{s}^{2}}.\] If M1 = 10 kg, M2 = 5 kg, q = 30o, what is the acceleration of mass M2
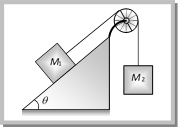
(a) \[10m{{s}^{-2}}\] (b) \[5m{{s}^{-2}}\] (c) \[\frac{2}{3}\,m{{s}^{-2}}\] (d) Zero Solution: (d) Acceleration \[=\frac{{{m}_{2}}-{{m}_{1}}\sin \theta }{{{m}_{1}}+{{m}_{2}}}g\]\[=\frac{5-10\,.\,\sin 30}{5+10}\,g\] \[=\frac{5-5}{5+10}\,g~=\text{ }0\] Problem 57. In the above problem, what is the tension in the string (a) 100 N (b) 50 N (c) 25 N (d) Zero Solution: (b) \[T=\frac{{{m}_{1}}{{m}_{2}}\left( 1+\sin \theta \right)}{{{m}_{1}}+{{m}_{2}}}g\] \[=\frac{10\times 5\left( 1+\sin 30 \right)\,.\,10}{10+5}=50\,N\] Problem 58. In the above problem, given that \[{{\operatorname{M}}_{2}}= 2{{M}_{1}}\,\,and {{M}_{2}}\] moves vertically downwards with acceleration a. If the position of the masses are reversed the acceleration of \[{{M}_{2}}\] down the inclined plane will be (a) 2 a (b) a (c) a/2 (d) None of the above Solution: (d) If \[{{m}_{2}}=2{{m}_{1}}\], then \[{{m}_{2}}\] moves vertically downward with acceleration \[a=\frac{{{m}_{2}}-{{m}_{1}}\,\sin \theta }{{{m}_{1}}+{{m}_{2}}}\,g=\frac{2{{m}_{1}}-{{m}_{1}}\,\sin \,30}{{{m}_{1}}+2{{m}_{1}}}\,g=\text{ }g/2\] If the position of masses are reversed then \[{{m}_{2}}\] moves downward with acceleration \[a'=\frac{{{m}_{2}}\sin \theta -{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\frac{2{{m}_{1}}\,\sin 30-{{m}_{1}}}{{{m}_{1}}+2{{m}_{1}}}\,.\,g=0\] [As \[{{\operatorname{m}}_{2}}= 2{{m}_{1}}\]] i.e. the \[{{m}_{2}}\] will not move. Problem 59. In the above problem, given that \[{{\operatorname{M}}_{2}}= 2{{M}_{1}}\] and the tension in the string is T. If the positions of the masses are reversed, the tension in the string will be (a) 4 T (b) 1 T (c) T (d) T/2 Solution : (c) Tension in the string \[T=\frac{{{m}_{1}}{{m}_{2}}\,\left( 1+\sin \theta \right)}{{{m}_{1}}+{{m}_{2}}}\,g\] If the position of the masses are reversed then there will be no effect on tension. Problem 60. In the above problem, given that \[{{\operatorname{M}}_{1}}= {{M}_{2}}\] and \[\theta ={{30}^{o}}\]. What will be the acceleration of the system (a) \[10\,\,m{{s}^{-2}}\] (b) \[5\,\,m{{s}^{-2}}\] (c) \[2.5\,\,m{{s}^{-2}}\] (d) Zero Solution: (c) \[a=\frac{{{m}_{2}}-{{m}_{1}}\,\sin \theta }{{{m}_{1}}+{{m}_{2}}}\,g\] \[=\frac{1-\sin 30}{2}\,g\] \[=\frac{g}{4}\,=\,2.5\,m/{{s}^{2}}\] [As \[{{\operatorname{m}}_{1}}= {{m}_{2}}\]] Problem 61. In the above problem, given that \[{{\operatorname{M}}_{1}}= {{M}_{2}}= 5 kg\] and \[\theta ={{30}^{o}}\]. What is tension in the string (a) 37.5 N (b) 25 N (c) 12.5 N (d) Zero Solution: (a) \[T=\frac{{{m}_{1}}{{m}_{2}}\,\left( 1+\sin \theta \right)}{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\frac{5\times 5\,\left( 1+\sin \,30 \right)}{5+5}\,\times \,10\]\[=37.5\,N\] Problem 62. Two blocks are attached to the two ends of a string passing over a smooth pulley as shown in the figure. The acceleration of the block will be \[\left( in m/{{s}^{2}} \right) \left( sin 3{{7}^{o}}= 0.60, sin 5{{3}^{o}}= 0.80 \right)\]
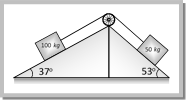
(a) 0.33 (b) 0.133 (c) 1 (d) 0.066 Solution: (b) \[a=\frac{{{m}_{2}}\,\sin \beta -{{m}_{1}}\,\sin \,\alpha }{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\frac{50\,\sin \,53{}^\circ -100\,\sin \,37{}^\circ }{100+50}\,g\]\[=-\,0.133\,m/{{s}^{2}}\] Problem 63. The two pulley arrangements shown in the figure are identical. The mass of the rope is negligible. In (a) the mass m is lifted up by attaching a mass 2m to the other end of the rope. In (b). m is lifted up by pulling the other end of the rope with a constant downward force of 2mg. The ratio of accelerations in two cases will be
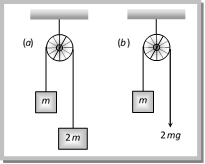
(a) 1 : 1 (b) 1 : 2 (c) 1 : 3 (d) 1 : 4 Solution: (c) For first case \[{{a}_{1}}=\frac{{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}g=\frac{2m-m}{m+2m}\,=\,\frac{g}{3}\] ?.. (i) For second case from free body diagram of m
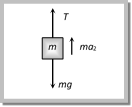
\[m{{a}_{2}}=T-mg\] \[m{{a}_{2}}=2mg-mg\] [As T = 2 mg] \[{{a}_{2}}=g\] ??..(ii) From (i) and (ii) \[\frac{{{a}_{1}}}{{{a}_{2}}}\,=\,\frac{g/3}{g}=\,1/3\] Problem 64. In the adjoining figure \[{{\operatorname{m}}_{1}}= 4{{m}_{2}}\]. The pulleys are smooth and light. At time t = 0, the system is at rest. If the system is released and if the acceleration of mass \[{{m}_{1}}\] is a, then the acceleration of \[{{m}_{2}}\] will be
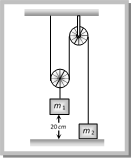
(a) g (b) a (c) \[\frac{a}{2}\] (d) 2a Solution: (d) Since the mass \[{{m}_{2}}\] travels double distance in comparison to mass \[{{m}_{1}}\] therefore its acceleration will be double i.e. 2a Problem 65. In the above problem (64), the value of a will be (a) g (b) \[\frac{g}{2}\] (c) \[\frac{g}{4}\] (d) \[\frac{g}{8}\]
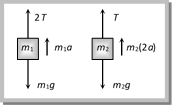
Solution: (c) By drawing the FBD of \[{{m}_{1}}\] and \[{{m}_{2}}\] \[{{m}_{1}}a={{m}_{1}}g-2T\] ?.. (i) \[{{m}_{2}}\left( 2a \right)=T-{{m}_{2}}g\] ?.. (ii) by solving these equation \[a=g/4\] Problem 66. In the above problem, the tension T in the string will be (a) \[{{\operatorname{m}}_{2}}g\] (b) \[\frac{{{m}_{2}}g}{2}\] (c) \[\frac{2}{3}{{m}_{2}}g\] (d) \[\frac{3}{2}{{m}_{2}}g\] Solution: (d) From the solution (65) by solving equation \[T=\frac{3}{2}\,{{m}_{2}}g\] Problem 67. In the above problem, the time taken by m1 in coming to rest position will be (a) 0.2 s (b) 0.4 s (c) 0.6 s (d) 0.8 s Solution: (b) Time taken by mass \[{{m}_{2}}\] to cover the distance 20 cm \[t=\sqrt{\frac{2h}{a}}\,=\,\sqrt{\frac{2\times 0.2}{g/4}}\,=\,\sqrt{\frac{2\times 0.2}{2.5}}\]\[=0.4\,\sec \] Problem 68. In the above problem, the distance covered by m2 in 0.4 s will be (a) 40 cm (b) 20 cm (c) 10 cm (d) 80 cm Solution: (a) Since the \[{{m}_{2}}\] mass cover double distance therefore \[\operatorname{S} = 2\,\,\times \,\,20 = 40 cm\] Problem 69. In the above problem, the velocity acquired by m2 in 0.4 second will be (a) 100 cm/s (b) 200 cm/s (c) 300 cm/s (d) 400 cm/s Solution: (b) Velocity acquired by mass \[{{m}_{2}}\] in 0.4 sec From \[v=u+at\] [As \[a=g/2=\frac{10}{2}=5\,m/{{s}^{2}}\]] \[v=0+5\times 0.4\] \[=2m/s\,\,=\,200\,cm/sec.\] Problem 70. In the above problem, the additional distance traversed by m2 in coming to rest position will be (a) 20 cm (b) 40 cm (c) 60 cm (d) 80 cm Solution: (a) When \[{{m}_{2}}\] mass acquired velocity 200 cm/sec it will move upward till its velocity becomes zero. \[H=\frac{{{v}^{2}}}{2g}=\frac{{{\left( 200 \right)}^{2}}}{2\times 100}\,=\,20\,cm\] Problem 71. The acceleration of block B in the figure will be
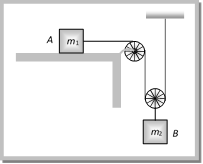
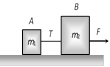
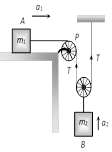
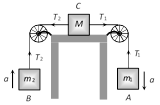
(a) \[\frac{{{m}_{2}}g}{(4{{m}_{1}}+{{m}_{2}})}\] (b) \[\frac{2{{m}_{2}}g}{(4{{m}_{1}}+{{m}_{2}})}\] (c) \[\frac{2{{m}_{1}}g}{({{m}_{1}}+4{{m}_{2}})}\] (d) \[\frac{2{{m}_{1}}g}{({{m}_{1}}+{{m}_{2}})}\] Solution: (a) When the block \[{{m}_{2}}\] moves downward with acceleration a, the acceleration of mass \[{{m}_{1}}\] will be \[2a\] because it covers double distance in the same time in comparison to \[{{m}_{2}}\].
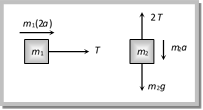
Let T is the tension in the string. By drawing the free body diagram of A and B \[T={{m}_{1}}2a\] ??.. (i) \[{{m}_{2}}g-2T={{m}_{2}}a\] ??.. (ii) by solving (i) and (ii) \[a=\frac{{{M}_{2}}g}{\left( 4{{m}_{1}}+{{m}_{2}} \right)}\]










 (a) 5 N (b) 4 N (c) 2 N (d) None of the above Solution: (c) Let \[{{m}_{1}}=6kg,\,{{m}_{2}}=4kg\] and \[F=5N\] (given) Force on the lighter mass = \[\frac{{{m}_{2}}\times F}{{{m}_{1}}+{{m}_{2}}}\]\[=\frac{4\times 5}{6+4}\]\[=2N\] Problem 44. In the above problem, if a push of 5 N is applied on the lighter mass, the force exerted by the lighter mass on the heavier mass will be (a) 5 N (b) 4 N (c) 2 N (d) None of the above Solution: (d) Force on the heavier mass \[=\frac{{{m}_{1}}F}{{{m}_{1}}+{{m}_{2}}}\]\[=\frac{6\times 5}{6+4}\] \[=3N\] Problem 45. In the above problem, the acceleration of the lighter mass will be (a) \[0.5\,m{{s}^{-2}}\] (b) \[\frac{5}{4}\,\,m{{s}^{-2}}\] (c) \[\frac{5}{6}\,\,m{{s}^{-2}}\] (d) None of the above Solution: (a) \[\text{Acceleration}=\frac{\text{Net force on the system}}{\text{Total mass of the system}}\]\[=\frac{5}{10}=0.5\,m/{{s}^{2}}\] Problem 46. Two blocks are in contact on a frictionless table one has a mass m and the other 2 m as shown in figure. Force F is applied on mass 2m then system moves towards right. Now the same force F is applied on m. The ratio of force of contact between the two blocks will be in the two cases respectively.
(a) 5 N (b) 4 N (c) 2 N (d) None of the above Solution: (c) Let \[{{m}_{1}}=6kg,\,{{m}_{2}}=4kg\] and \[F=5N\] (given) Force on the lighter mass = \[\frac{{{m}_{2}}\times F}{{{m}_{1}}+{{m}_{2}}}\]\[=\frac{4\times 5}{6+4}\]\[=2N\] Problem 44. In the above problem, if a push of 5 N is applied on the lighter mass, the force exerted by the lighter mass on the heavier mass will be (a) 5 N (b) 4 N (c) 2 N (d) None of the above Solution: (d) Force on the heavier mass \[=\frac{{{m}_{1}}F}{{{m}_{1}}+{{m}_{2}}}\]\[=\frac{6\times 5}{6+4}\] \[=3N\] Problem 45. In the above problem, the acceleration of the lighter mass will be (a) \[0.5\,m{{s}^{-2}}\] (b) \[\frac{5}{4}\,\,m{{s}^{-2}}\] (c) \[\frac{5}{6}\,\,m{{s}^{-2}}\] (d) None of the above Solution: (a) \[\text{Acceleration}=\frac{\text{Net force on the system}}{\text{Total mass of the system}}\]\[=\frac{5}{10}=0.5\,m/{{s}^{2}}\] Problem 46. Two blocks are in contact on a frictionless table one has a mass m and the other 2 m as shown in figure. Force F is applied on mass 2m then system moves towards right. Now the same force F is applied on m. The ratio of force of contact between the two blocks will be in the two cases respectively.  (a) 1 : 1 (b) 1 : 2 (c) 1 : 3 (d) 1 : 4 Solution: (b) When the force is applied on mass 2m contact force \[{{f}_{1}}=\frac{m}{m+2m}g=\frac{g}{3}\] When the force is applied on mass m contact force \[{{f}_{2}}=\frac{2m}{m+2m}g=\frac{2}{3}g\] Ratio of contact forces \[\frac{{{f}_{1}}}{{{f}_{2}}}=\frac{1}{2}\] Motion of Blocks Connected by Mass Less String.
(a) 1 : 1 (b) 1 : 2 (c) 1 : 3 (d) 1 : 4 Solution: (b) When the force is applied on mass 2m contact force \[{{f}_{1}}=\frac{m}{m+2m}g=\frac{g}{3}\] When the force is applied on mass m contact force \[{{f}_{2}}=\frac{2m}{m+2m}g=\frac{2}{3}g\] Ratio of contact forces \[\frac{{{f}_{1}}}{{{f}_{2}}}=\frac{1}{2}\] Motion of Blocks Connected by Mass Less String. 









 (a) 1 N (b) 5 N (c) 8 N (d) 10 N Solution: (c) By comparing the above problem with general expression. \[{{T}_{1}}=\frac{\left( {{m}_{2}}+{{m}_{3}} \right)F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\] \[=\frac{\left( 3+5 \right)\,10}{2+3+5}\]\[=8\,Newton\] Problem 49. Two blocks are connected by a string as shown in the diagram. The upper block is hung by another string. A force F applied on the upper string produces an acceleration of \[2m/{{s}^{2}}\] in the upward direction in both the blocks. If T and \[{T}'\] be the tensions in the two parts of the string, then [AMU (Engg.) 2000]
(a) 1 N (b) 5 N (c) 8 N (d) 10 N Solution: (c) By comparing the above problem with general expression. \[{{T}_{1}}=\frac{\left( {{m}_{2}}+{{m}_{3}} \right)F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\] \[=\frac{\left( 3+5 \right)\,10}{2+3+5}\]\[=8\,Newton\] Problem 49. Two blocks are connected by a string as shown in the diagram. The upper block is hung by another string. A force F applied on the upper string produces an acceleration of \[2m/{{s}^{2}}\] in the upward direction in both the blocks. If T and \[{T}'\] be the tensions in the two parts of the string, then [AMU (Engg.) 2000]  (a) \[T=70.8N\] and \[{T}'=47.2N\] (b) \[T=58.8N\] and \[{T}'=47.2N\] (c) \[T=70.8N\] and \[{T}'=58.8N\] (d) \[T=70.8N\] and \[{T}'=0\]
(a) \[T=70.8N\] and \[{T}'=47.2N\] (b) \[T=58.8N\] and \[{T}'=47.2N\] (c) \[T=70.8N\] and \[{T}'=58.8N\] (d) \[T=70.8N\] and \[{T}'=0\]  Solution: (a) From F.B.D. of mass 4 kg \[4a=T'-4g\] .?. (i) From F.B.D. of mass 2 kg \[2a=T=T'-2g\] .?. (ii) For total system upward force \[F=T=\left( 2+4 \right)\,\left( g+a \right)\]\[=6\,\left( 18+2 \right)\,N\]= 70.8 N by substituting the value of T in equation (i) and (ii) and solving we get \[T'=47.2N\] Problem 50. Three masses of 15 kg. 10 kg and 5 kg are suspended vertically as shown in the fig. If the string attached to the support breaks and the system falls freely, what will be the tension in the string between 10 kg and 5 kg masses. Take \[g=10\,m{{s}^{-2}}\]. It is assumed that the string remains tight during the motion
Solution: (a) From F.B.D. of mass 4 kg \[4a=T'-4g\] .?. (i) From F.B.D. of mass 2 kg \[2a=T=T'-2g\] .?. (ii) For total system upward force \[F=T=\left( 2+4 \right)\,\left( g+a \right)\]\[=6\,\left( 18+2 \right)\,N\]= 70.8 N by substituting the value of T in equation (i) and (ii) and solving we get \[T'=47.2N\] Problem 50. Three masses of 15 kg. 10 kg and 5 kg are suspended vertically as shown in the fig. If the string attached to the support breaks and the system falls freely, what will be the tension in the string between 10 kg and 5 kg masses. Take \[g=10\,m{{s}^{-2}}\]. It is assumed that the string remains tight during the motion  (a) 300 N (b) 250 N (c) 50 N (d) Zero Solution: (d) In the condition of free fall, tension becomes zero. Problem 51. A sphere is accelerated upwards with the help of a cord whose breaking strength is five times its weight. The maximum acceleration with which the sphere can move up without cord breaking is (a) 4g (b) 3g (c) 2g (d) g Solution: (a) Tension in the cord \[= m\left( g + a \right)\] and breaking strength = 5 mg For critical condition \[m\left( g+a \right)\,=\,5mg\,\,\,\,\Rightarrow \,\,\,a=4g\] This is the maximum acceleration with which the sphere can move up with cord breaking.
(a) 300 N (b) 250 N (c) 50 N (d) Zero Solution: (d) In the condition of free fall, tension becomes zero. Problem 51. A sphere is accelerated upwards with the help of a cord whose breaking strength is five times its weight. The maximum acceleration with which the sphere can move up without cord breaking is (a) 4g (b) 3g (c) 2g (d) g Solution: (a) Tension in the cord \[= m\left( g + a \right)\] and breaking strength = 5 mg For critical condition \[m\left( g+a \right)\,=\,5mg\,\,\,\,\Rightarrow \,\,\,a=4g\] This is the maximum acceleration with which the sphere can move up with cord breaking. 







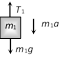
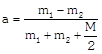
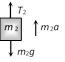
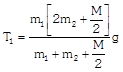
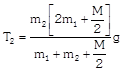












 As
As 




 (a) \[100\,m{{s}^{-2}}\] (b) \[3m{{s}^{-2}}\] (c) \[10m{{s}^{-2}}\] (d) \[30m{{s}^{-2}}\] Solution: (b) \[a=\left( \frac{{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right)\,g\] \[={{\left( \frac{3}{7+3} \right)}^{10}}=3m/{{s}^{2}}\] Problem 54. Two masses \[{{m}_{1}}\] and \[{{m}_{2}}\] are attached to a string which passes over a frictionless smooth pulley. When \[{{m}_{1}}=10\,kg,\] \[{{m}_{2}}=6\,kg,\,\]the acceleration of masses is [Orissa JEE 2002]
(a) \[100\,m{{s}^{-2}}\] (b) \[3m{{s}^{-2}}\] (c) \[10m{{s}^{-2}}\] (d) \[30m{{s}^{-2}}\] Solution: (b) \[a=\left( \frac{{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right)\,g\] \[={{\left( \frac{3}{7+3} \right)}^{10}}=3m/{{s}^{2}}\] Problem 54. Two masses \[{{m}_{1}}\] and \[{{m}_{2}}\] are attached to a string which passes over a frictionless smooth pulley. When \[{{m}_{1}}=10\,kg,\] \[{{m}_{2}}=6\,kg,\,\]the acceleration of masses is [Orissa JEE 2002]  (a) 20\[m/{{s}^{2}}\] (b) \[5m/{{s}^{2}}\] (c) 2.5\[m/{{s}^{2}}\] (d) \[10\,m/{{s}^{2}}\] Solution: (c) \[a=\frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\left( \frac{10-6}{10+6} \right)\,10\]\[=2.5\,m/{{s}^{2}}\] Problem 55. Two weights \[{{W}_{1}}\] and \[{{W}_{2}}\] are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up with an acceleration g, the tension in the string will be (a) \[\frac{4{{W}_{1}}{{W}_{2}}}{{{W}_{1}}+{{W}_{2}}}\] (b) \[\frac{2{{W}_{1}}{{W}_{2}}}{{{W}_{1}}+{{W}_{2}}}\] (c) \[\frac{{{W}_{1}}{{W}_{2}}}{{{W}_{1}}+{{W}_{2}}}\] (d) \[\frac{{{W}_{1}}{{W}_{2}}}{2\,({{W}_{1}}+{{W}_{2}})}\] Solution: (a) When the system is at rest tension in string \[T=\frac{2{{m}_{1}}{{m}_{2}}}{\left( {{m}_{1}}+{{m}_{2}} \right)}g\] If the system moves upward with acceleration g then \[T=\frac{2{{m}_{1}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}\left( g+g \right)\] \[=\frac{4{{m}_{1}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}g\] or \[T=\frac{4{{w}_{1}}{{w}_{2}}}{{{w}_{1}}+{{w}_{2}}}\] Problem 56. Two masses \[{{\operatorname{M}}_{1}}\,\,and {{M}_{2}}\] are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane in \[\theta \]. Take \[\operatorname{g} = 10 m{{s}^{2}}.\] If M1 = 10 kg, M2 = 5 kg, q = 30o, what is the acceleration of mass M2
(a) 20\[m/{{s}^{2}}\] (b) \[5m/{{s}^{2}}\] (c) 2.5\[m/{{s}^{2}}\] (d) \[10\,m/{{s}^{2}}\] Solution: (c) \[a=\frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\left( \frac{10-6}{10+6} \right)\,10\]\[=2.5\,m/{{s}^{2}}\] Problem 55. Two weights \[{{W}_{1}}\] and \[{{W}_{2}}\] are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up with an acceleration g, the tension in the string will be (a) \[\frac{4{{W}_{1}}{{W}_{2}}}{{{W}_{1}}+{{W}_{2}}}\] (b) \[\frac{2{{W}_{1}}{{W}_{2}}}{{{W}_{1}}+{{W}_{2}}}\] (c) \[\frac{{{W}_{1}}{{W}_{2}}}{{{W}_{1}}+{{W}_{2}}}\] (d) \[\frac{{{W}_{1}}{{W}_{2}}}{2\,({{W}_{1}}+{{W}_{2}})}\] Solution: (a) When the system is at rest tension in string \[T=\frac{2{{m}_{1}}{{m}_{2}}}{\left( {{m}_{1}}+{{m}_{2}} \right)}g\] If the system moves upward with acceleration g then \[T=\frac{2{{m}_{1}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}\left( g+g \right)\] \[=\frac{4{{m}_{1}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}g\] or \[T=\frac{4{{w}_{1}}{{w}_{2}}}{{{w}_{1}}+{{w}_{2}}}\] Problem 56. Two masses \[{{\operatorname{M}}_{1}}\,\,and {{M}_{2}}\] are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane in \[\theta \]. Take \[\operatorname{g} = 10 m{{s}^{2}}.\] If M1 = 10 kg, M2 = 5 kg, q = 30o, what is the acceleration of mass M2  (a) \[10m{{s}^{-2}}\] (b) \[5m{{s}^{-2}}\] (c) \[\frac{2}{3}\,m{{s}^{-2}}\] (d) Zero Solution: (d) Acceleration \[=\frac{{{m}_{2}}-{{m}_{1}}\sin \theta }{{{m}_{1}}+{{m}_{2}}}g\]\[=\frac{5-10\,.\,\sin 30}{5+10}\,g\] \[=\frac{5-5}{5+10}\,g~=\text{ }0\] Problem 57. In the above problem, what is the tension in the string (a) 100 N (b) 50 N (c) 25 N (d) Zero Solution: (b) \[T=\frac{{{m}_{1}}{{m}_{2}}\left( 1+\sin \theta \right)}{{{m}_{1}}+{{m}_{2}}}g\] \[=\frac{10\times 5\left( 1+\sin 30 \right)\,.\,10}{10+5}=50\,N\] Problem 58. In the above problem, given that \[{{\operatorname{M}}_{2}}= 2{{M}_{1}}\,\,and {{M}_{2}}\] moves vertically downwards with acceleration a. If the position of the masses are reversed the acceleration of \[{{M}_{2}}\] down the inclined plane will be (a) 2 a (b) a (c) a/2 (d) None of the above Solution: (d) If \[{{m}_{2}}=2{{m}_{1}}\], then \[{{m}_{2}}\] moves vertically downward with acceleration \[a=\frac{{{m}_{2}}-{{m}_{1}}\,\sin \theta }{{{m}_{1}}+{{m}_{2}}}\,g=\frac{2{{m}_{1}}-{{m}_{1}}\,\sin \,30}{{{m}_{1}}+2{{m}_{1}}}\,g=\text{ }g/2\] If the position of masses are reversed then \[{{m}_{2}}\] moves downward with acceleration \[a'=\frac{{{m}_{2}}\sin \theta -{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\frac{2{{m}_{1}}\,\sin 30-{{m}_{1}}}{{{m}_{1}}+2{{m}_{1}}}\,.\,g=0\] [As \[{{\operatorname{m}}_{2}}= 2{{m}_{1}}\]] i.e. the \[{{m}_{2}}\] will not move. Problem 59. In the above problem, given that \[{{\operatorname{M}}_{2}}= 2{{M}_{1}}\] and the tension in the string is T. If the positions of the masses are reversed, the tension in the string will be (a) 4 T (b) 1 T (c) T (d) T/2 Solution : (c) Tension in the string \[T=\frac{{{m}_{1}}{{m}_{2}}\,\left( 1+\sin \theta \right)}{{{m}_{1}}+{{m}_{2}}}\,g\] If the position of the masses are reversed then there will be no effect on tension. Problem 60. In the above problem, given that \[{{\operatorname{M}}_{1}}= {{M}_{2}}\] and \[\theta ={{30}^{o}}\]. What will be the acceleration of the system (a) \[10\,\,m{{s}^{-2}}\] (b) \[5\,\,m{{s}^{-2}}\] (c) \[2.5\,\,m{{s}^{-2}}\] (d) Zero Solution: (c) \[a=\frac{{{m}_{2}}-{{m}_{1}}\,\sin \theta }{{{m}_{1}}+{{m}_{2}}}\,g\] \[=\frac{1-\sin 30}{2}\,g\] \[=\frac{g}{4}\,=\,2.5\,m/{{s}^{2}}\] [As \[{{\operatorname{m}}_{1}}= {{m}_{2}}\]] Problem 61. In the above problem, given that \[{{\operatorname{M}}_{1}}= {{M}_{2}}= 5 kg\] and \[\theta ={{30}^{o}}\]. What is tension in the string (a) 37.5 N (b) 25 N (c) 12.5 N (d) Zero Solution: (a) \[T=\frac{{{m}_{1}}{{m}_{2}}\,\left( 1+\sin \theta \right)}{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\frac{5\times 5\,\left( 1+\sin \,30 \right)}{5+5}\,\times \,10\]\[=37.5\,N\] Problem 62. Two blocks are attached to the two ends of a string passing over a smooth pulley as shown in the figure. The acceleration of the block will be \[\left( in m/{{s}^{2}} \right) \left( sin 3{{7}^{o}}= 0.60, sin 5{{3}^{o}}= 0.80 \right)\]
(a) \[10m{{s}^{-2}}\] (b) \[5m{{s}^{-2}}\] (c) \[\frac{2}{3}\,m{{s}^{-2}}\] (d) Zero Solution: (d) Acceleration \[=\frac{{{m}_{2}}-{{m}_{1}}\sin \theta }{{{m}_{1}}+{{m}_{2}}}g\]\[=\frac{5-10\,.\,\sin 30}{5+10}\,g\] \[=\frac{5-5}{5+10}\,g~=\text{ }0\] Problem 57. In the above problem, what is the tension in the string (a) 100 N (b) 50 N (c) 25 N (d) Zero Solution: (b) \[T=\frac{{{m}_{1}}{{m}_{2}}\left( 1+\sin \theta \right)}{{{m}_{1}}+{{m}_{2}}}g\] \[=\frac{10\times 5\left( 1+\sin 30 \right)\,.\,10}{10+5}=50\,N\] Problem 58. In the above problem, given that \[{{\operatorname{M}}_{2}}= 2{{M}_{1}}\,\,and {{M}_{2}}\] moves vertically downwards with acceleration a. If the position of the masses are reversed the acceleration of \[{{M}_{2}}\] down the inclined plane will be (a) 2 a (b) a (c) a/2 (d) None of the above Solution: (d) If \[{{m}_{2}}=2{{m}_{1}}\], then \[{{m}_{2}}\] moves vertically downward with acceleration \[a=\frac{{{m}_{2}}-{{m}_{1}}\,\sin \theta }{{{m}_{1}}+{{m}_{2}}}\,g=\frac{2{{m}_{1}}-{{m}_{1}}\,\sin \,30}{{{m}_{1}}+2{{m}_{1}}}\,g=\text{ }g/2\] If the position of masses are reversed then \[{{m}_{2}}\] moves downward with acceleration \[a'=\frac{{{m}_{2}}\sin \theta -{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\frac{2{{m}_{1}}\,\sin 30-{{m}_{1}}}{{{m}_{1}}+2{{m}_{1}}}\,.\,g=0\] [As \[{{\operatorname{m}}_{2}}= 2{{m}_{1}}\]] i.e. the \[{{m}_{2}}\] will not move. Problem 59. In the above problem, given that \[{{\operatorname{M}}_{2}}= 2{{M}_{1}}\] and the tension in the string is T. If the positions of the masses are reversed, the tension in the string will be (a) 4 T (b) 1 T (c) T (d) T/2 Solution : (c) Tension in the string \[T=\frac{{{m}_{1}}{{m}_{2}}\,\left( 1+\sin \theta \right)}{{{m}_{1}}+{{m}_{2}}}\,g\] If the position of the masses are reversed then there will be no effect on tension. Problem 60. In the above problem, given that \[{{\operatorname{M}}_{1}}= {{M}_{2}}\] and \[\theta ={{30}^{o}}\]. What will be the acceleration of the system (a) \[10\,\,m{{s}^{-2}}\] (b) \[5\,\,m{{s}^{-2}}\] (c) \[2.5\,\,m{{s}^{-2}}\] (d) Zero Solution: (c) \[a=\frac{{{m}_{2}}-{{m}_{1}}\,\sin \theta }{{{m}_{1}}+{{m}_{2}}}\,g\] \[=\frac{1-\sin 30}{2}\,g\] \[=\frac{g}{4}\,=\,2.5\,m/{{s}^{2}}\] [As \[{{\operatorname{m}}_{1}}= {{m}_{2}}\]] Problem 61. In the above problem, given that \[{{\operatorname{M}}_{1}}= {{M}_{2}}= 5 kg\] and \[\theta ={{30}^{o}}\]. What is tension in the string (a) 37.5 N (b) 25 N (c) 12.5 N (d) Zero Solution: (a) \[T=\frac{{{m}_{1}}{{m}_{2}}\,\left( 1+\sin \theta \right)}{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\frac{5\times 5\,\left( 1+\sin \,30 \right)}{5+5}\,\times \,10\]\[=37.5\,N\] Problem 62. Two blocks are attached to the two ends of a string passing over a smooth pulley as shown in the figure. The acceleration of the block will be \[\left( in m/{{s}^{2}} \right) \left( sin 3{{7}^{o}}= 0.60, sin 5{{3}^{o}}= 0.80 \right)\]  (a) 0.33 (b) 0.133 (c) 1 (d) 0.066 Solution: (b) \[a=\frac{{{m}_{2}}\,\sin \beta -{{m}_{1}}\,\sin \,\alpha }{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\frac{50\,\sin \,53{}^\circ -100\,\sin \,37{}^\circ }{100+50}\,g\]\[=-\,0.133\,m/{{s}^{2}}\] Problem 63. The two pulley arrangements shown in the figure are identical. The mass of the rope is negligible. In (a) the mass m is lifted up by attaching a mass 2m to the other end of the rope. In (b). m is lifted up by pulling the other end of the rope with a constant downward force of 2mg. The ratio of accelerations in two cases will be
(a) 0.33 (b) 0.133 (c) 1 (d) 0.066 Solution: (b) \[a=\frac{{{m}_{2}}\,\sin \beta -{{m}_{1}}\,\sin \,\alpha }{{{m}_{1}}+{{m}_{2}}}\,g\]\[=\frac{50\,\sin \,53{}^\circ -100\,\sin \,37{}^\circ }{100+50}\,g\]\[=-\,0.133\,m/{{s}^{2}}\] Problem 63. The two pulley arrangements shown in the figure are identical. The mass of the rope is negligible. In (a) the mass m is lifted up by attaching a mass 2m to the other end of the rope. In (b). m is lifted up by pulling the other end of the rope with a constant downward force of 2mg. The ratio of accelerations in two cases will be  (a) 1 : 1 (b) 1 : 2 (c) 1 : 3 (d) 1 : 4 Solution: (c) For first case \[{{a}_{1}}=\frac{{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}g=\frac{2m-m}{m+2m}\,=\,\frac{g}{3}\] ?.. (i) For second case from free body diagram of m
(a) 1 : 1 (b) 1 : 2 (c) 1 : 3 (d) 1 : 4 Solution: (c) For first case \[{{a}_{1}}=\frac{{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}g=\frac{2m-m}{m+2m}\,=\,\frac{g}{3}\] ?.. (i) For second case from free body diagram of m  \[m{{a}_{2}}=T-mg\] \[m{{a}_{2}}=2mg-mg\] [As T = 2 mg] \[{{a}_{2}}=g\] ??..(ii) From (i) and (ii) \[\frac{{{a}_{1}}}{{{a}_{2}}}\,=\,\frac{g/3}{g}=\,1/3\] Problem 64. In the adjoining figure \[{{\operatorname{m}}_{1}}= 4{{m}_{2}}\]. The pulleys are smooth and light. At time t = 0, the system is at rest. If the system is released and if the acceleration of mass \[{{m}_{1}}\] is a, then the acceleration of \[{{m}_{2}}\] will be
\[m{{a}_{2}}=T-mg\] \[m{{a}_{2}}=2mg-mg\] [As T = 2 mg] \[{{a}_{2}}=g\] ??..(ii) From (i) and (ii) \[\frac{{{a}_{1}}}{{{a}_{2}}}\,=\,\frac{g/3}{g}=\,1/3\] Problem 64. In the adjoining figure \[{{\operatorname{m}}_{1}}= 4{{m}_{2}}\]. The pulleys are smooth and light. At time t = 0, the system is at rest. If the system is released and if the acceleration of mass \[{{m}_{1}}\] is a, then the acceleration of \[{{m}_{2}}\] will be  (a) g (b) a (c) \[\frac{a}{2}\] (d) 2a Solution: (d) Since the mass \[{{m}_{2}}\] travels double distance in comparison to mass \[{{m}_{1}}\] therefore its acceleration will be double i.e. 2a Problem 65. In the above problem (64), the value of a will be (a) g (b) \[\frac{g}{2}\] (c) \[\frac{g}{4}\] (d) \[\frac{g}{8}\]
(a) g (b) a (c) \[\frac{a}{2}\] (d) 2a Solution: (d) Since the mass \[{{m}_{2}}\] travels double distance in comparison to mass \[{{m}_{1}}\] therefore its acceleration will be double i.e. 2a Problem 65. In the above problem (64), the value of a will be (a) g (b) \[\frac{g}{2}\] (c) \[\frac{g}{4}\] (d) \[\frac{g}{8}\]  Solution: (c) By drawing the FBD of \[{{m}_{1}}\] and \[{{m}_{2}}\] \[{{m}_{1}}a={{m}_{1}}g-2T\] ?.. (i) \[{{m}_{2}}\left( 2a \right)=T-{{m}_{2}}g\] ?.. (ii) by solving these equation \[a=g/4\] Problem 66. In the above problem, the tension T in the string will be (a) \[{{\operatorname{m}}_{2}}g\] (b) \[\frac{{{m}_{2}}g}{2}\] (c) \[\frac{2}{3}{{m}_{2}}g\] (d) \[\frac{3}{2}{{m}_{2}}g\] Solution: (d) From the solution (65) by solving equation \[T=\frac{3}{2}\,{{m}_{2}}g\] Problem 67. In the above problem, the time taken by m1 in coming to rest position will be (a) 0.2 s (b) 0.4 s (c) 0.6 s (d) 0.8 s Solution: (b) Time taken by mass \[{{m}_{2}}\] to cover the distance 20 cm \[t=\sqrt{\frac{2h}{a}}\,=\,\sqrt{\frac{2\times 0.2}{g/4}}\,=\,\sqrt{\frac{2\times 0.2}{2.5}}\]\[=0.4\,\sec \] Problem 68. In the above problem, the distance covered by m2 in 0.4 s will be (a) 40 cm (b) 20 cm (c) 10 cm (d) 80 cm Solution: (a) Since the \[{{m}_{2}}\] mass cover double distance therefore \[\operatorname{S} = 2\,\,\times \,\,20 = 40 cm\] Problem 69. In the above problem, the velocity acquired by m2 in 0.4 second will be (a) 100 cm/s (b) 200 cm/s (c) 300 cm/s (d) 400 cm/s Solution: (b) Velocity acquired by mass \[{{m}_{2}}\] in 0.4 sec From \[v=u+at\] [As \[a=g/2=\frac{10}{2}=5\,m/{{s}^{2}}\]] \[v=0+5\times 0.4\] \[=2m/s\,\,=\,200\,cm/sec.\] Problem 70. In the above problem, the additional distance traversed by m2 in coming to rest position will be (a) 20 cm (b) 40 cm (c) 60 cm (d) 80 cm Solution: (a) When \[{{m}_{2}}\] mass acquired velocity 200 cm/sec it will move upward till its velocity becomes zero. \[H=\frac{{{v}^{2}}}{2g}=\frac{{{\left( 200 \right)}^{2}}}{2\times 100}\,=\,20\,cm\] Problem 71. The acceleration of block B in the figure will be
Solution: (c) By drawing the FBD of \[{{m}_{1}}\] and \[{{m}_{2}}\] \[{{m}_{1}}a={{m}_{1}}g-2T\] ?.. (i) \[{{m}_{2}}\left( 2a \right)=T-{{m}_{2}}g\] ?.. (ii) by solving these equation \[a=g/4\] Problem 66. In the above problem, the tension T in the string will be (a) \[{{\operatorname{m}}_{2}}g\] (b) \[\frac{{{m}_{2}}g}{2}\] (c) \[\frac{2}{3}{{m}_{2}}g\] (d) \[\frac{3}{2}{{m}_{2}}g\] Solution: (d) From the solution (65) by solving equation \[T=\frac{3}{2}\,{{m}_{2}}g\] Problem 67. In the above problem, the time taken by m1 in coming to rest position will be (a) 0.2 s (b) 0.4 s (c) 0.6 s (d) 0.8 s Solution: (b) Time taken by mass \[{{m}_{2}}\] to cover the distance 20 cm \[t=\sqrt{\frac{2h}{a}}\,=\,\sqrt{\frac{2\times 0.2}{g/4}}\,=\,\sqrt{\frac{2\times 0.2}{2.5}}\]\[=0.4\,\sec \] Problem 68. In the above problem, the distance covered by m2 in 0.4 s will be (a) 40 cm (b) 20 cm (c) 10 cm (d) 80 cm Solution: (a) Since the \[{{m}_{2}}\] mass cover double distance therefore \[\operatorname{S} = 2\,\,\times \,\,20 = 40 cm\] Problem 69. In the above problem, the velocity acquired by m2 in 0.4 second will be (a) 100 cm/s (b) 200 cm/s (c) 300 cm/s (d) 400 cm/s Solution: (b) Velocity acquired by mass \[{{m}_{2}}\] in 0.4 sec From \[v=u+at\] [As \[a=g/2=\frac{10}{2}=5\,m/{{s}^{2}}\]] \[v=0+5\times 0.4\] \[=2m/s\,\,=\,200\,cm/sec.\] Problem 70. In the above problem, the additional distance traversed by m2 in coming to rest position will be (a) 20 cm (b) 40 cm (c) 60 cm (d) 80 cm Solution: (a) When \[{{m}_{2}}\] mass acquired velocity 200 cm/sec it will move upward till its velocity becomes zero. \[H=\frac{{{v}^{2}}}{2g}=\frac{{{\left( 200 \right)}^{2}}}{2\times 100}\,=\,20\,cm\] Problem 71. The acceleration of block B in the figure will be  (a) \[\frac{{{m}_{2}}g}{(4{{m}_{1}}+{{m}_{2}})}\] (b) \[\frac{2{{m}_{2}}g}{(4{{m}_{1}}+{{m}_{2}})}\] (c) \[\frac{2{{m}_{1}}g}{({{m}_{1}}+4{{m}_{2}})}\] (d) \[\frac{2{{m}_{1}}g}{({{m}_{1}}+{{m}_{2}})}\] Solution: (a) When the block \[{{m}_{2}}\] moves downward with acceleration a, the acceleration of mass \[{{m}_{1}}\] will be \[2a\] because it covers double distance in the same time in comparison to \[{{m}_{2}}\].
(a) \[\frac{{{m}_{2}}g}{(4{{m}_{1}}+{{m}_{2}})}\] (b) \[\frac{2{{m}_{2}}g}{(4{{m}_{1}}+{{m}_{2}})}\] (c) \[\frac{2{{m}_{1}}g}{({{m}_{1}}+4{{m}_{2}})}\] (d) \[\frac{2{{m}_{1}}g}{({{m}_{1}}+{{m}_{2}})}\] Solution: (a) When the block \[{{m}_{2}}\] moves downward with acceleration a, the acceleration of mass \[{{m}_{1}}\] will be \[2a\] because it covers double distance in the same time in comparison to \[{{m}_{2}}\].  Let T is the tension in the string. By drawing the free body diagram of A and B \[T={{m}_{1}}2a\] ??.. (i) \[{{m}_{2}}g-2T={{m}_{2}}a\] ??.. (ii) by solving (i) and (ii) \[a=\frac{{{M}_{2}}g}{\left( 4{{m}_{1}}+{{m}_{2}} \right)}\]
Let T is the tension in the string. By drawing the free body diagram of A and B \[T={{m}_{1}}2a\] ??.. (i) \[{{m}_{2}}g-2T={{m}_{2}}a\] ??.. (ii) by solving (i) and (ii) \[a=\frac{{{M}_{2}}g}{\left( 4{{m}_{1}}+{{m}_{2}} \right)}\]
