JEE Main & Advanced Mathematics Vector Algebra Scalar Triple Product

(1) Scalar triple product of three vectors : If \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] are three vectors, then their scalar triple product is defined as the dot product of two vectors \[\mathbf{a}\] and \[\mathbf{b\times c}\]. It is generally denoted by \[\mathbf{a}\]. \[\mathbf{(b\times c)}\] or \[\mathbf{[a}\,\,\mathbf{b}\,\,\,\mathbf{c]}\].

(2) Properties of scalar triple product

(i) If \[\mathbf{a},\,\mathbf{b},\mathbf{c}\] are cyclically permuted, the value of scalar triple product remains the same. i.e., \[(\mathbf{a}\times \mathbf{b})\,.\,\mathbf{c}=(\mathbf{b}\times \mathbf{c})\,.\,\mathbf{a}=(\mathbf{c}\times \mathbf{a})\,.\,\mathbf{b}\] or \[[\mathbf{a}\,\mathbf{b}\,\mathbf{c}]=[\mathbf{b}\,\mathbf{c}\,\mathbf{a}]=[\mathbf{c}\,\mathbf{a}\,\mathbf{b}]\]

(ii) The change of cyclic order of vectors in scalar triple product changes the sign of the scalar triple product but not the magnitude i.e., \[[\mathbf{a}\,\mathbf{b}\,\mathbf{c}]=-[\mathbf{b}\,\mathbf{a}\,\mathbf{c}]=-[\mathbf{c}\,\mathbf{b}\,\mathbf{a}]=-[\mathbf{a}\,\mathbf{c}\,\mathbf{b}]\]

(iii) In scalar triple product the positions of dot and cross can be interchanged provided that the cyclic order of the vectors remains same i.e., \[(\mathbf{a}\times \mathbf{b})\,.\,\mathbf{c}=\mathbf{a}\,.\,(\mathbf{b}\times \mathbf{c})\]

(iv) The scalar triple product of three vectors is zero if any two of them are equal.

(v) For any three vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] and scalar \[\lambda \], \[[\lambda \,\mathbf{a}\,\mathbf{b}\,\mathbf{c}]\,\] \[=\,\lambda [\mathbf{a}\,\mathbf{b}\,\mathbf{c}]\]

(vi) The scalar triple product of three vectors is zero if any two of them are parallel or collinear.

(vii) If \[\mathbf{a},\,\mathbf{b},\,\mathbf{c},\,\mathbf{d}\] are four vectors, then \[[(\mathbf{a}+\mathbf{b})\,\,\mathbf{c}\,\,\mathbf{d}]=\] \[[\mathbf{a}\,\mathbf{c}\,\mathbf{d}]+\mathbf{[b}\text{ }\mathbf{c}\text{ }\mathbf{d}]\]

(viii) The necessary and sufficient condition for three non-zero non-collinear vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] to be coplanar is that \[[\mathbf{a}\,\mathbf{b}\,\mathbf{c}]=0\].

(ix) Four points with position vectors \[\mathbf{a,}\,\,\mathbf{b,}\,\,\mathbf{c}\] and \[\mathbf{d}\] will be coplanar, if \[[\mathbf{a}\,\,\mathbf{b}\ \,\mathbf{c}]+[\mathbf{d}\,\,\mathbf{c}\,\,\mathbf{a}]+[\mathbf{d}\ \,\mathbf{a}\,\,\mathbf{b}]\]\[=[\mathbf{a}\,\ \mathbf{b}\,\ \mathbf{c}]\].

(x) Volume of parallelopiped whose coterminous edges are \[\mathbf{a,}\,\,\mathbf{b,}\,\,\mathbf{c}\] is \[[\mathbf{a}\,\mathbf{b}\,\mathbf{c}]\]or  \[\mathbf{a}\,\mathbf{(b\times c)}\].

(3) Scalar triple product in terms of components

(i) If \[\mathbf{a}={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k},\,\,\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\] and \[\mathbf{c}={{c}_{1}}\mathbf{i}+{{c}_{2}}\mathbf{j}+{{c}_{3}}\mathbf{k}\] be three vectors then, \[[\mathbf{a}\,\mathbf{b}\,\mathbf{c}]=\left| \,\begin{matrix} {{a}_{1}} & {{b}_{1}} & {{c}_{1}}  \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}}  \\ {{a}_{3}} & {{b}_{3}} & {{c}_{3}}  \\ \end{matrix}\, \right|\]

(ii) If \[\mathbf{a}={{a}_{1}}\mathbf{l}+{{a}_{2}}\mathbf{m}+{{a}_{3}}\mathbf{n},\,\mathbf{b}={{b}_{1}}\mathbf{l}+{{b}_{2}}\mathbf{m}+{{b}_{3}}\mathbf{n}\]  and \[\mathbf{c}={{c}_{1}}\mathbf{l}+{{c}_{2}}\mathbf{m}+{{c}_{3}}\mathbf{n}\], then \[[\mathbf{a}\,\mathbf{b}\,\mathbf{c}]=\left| \begin{matrix} {{a}_{1}} & {{a}_{2}} & {{a}_{3}}  \\ {{b}_{1}} & {{b}_{2}} & {{b}_{3}}  \\ {{c}_{1}} & {{c}_{2}} & {{c}_{3}}  \\ \end{matrix}\, \right|\,[\mathbf{l}\,\mathbf{m}\,\mathbf{n}]\]

(iii) For any three vectors \[\mathbf{a},\,\mathbf{b}\] and \[\mathbf{c}\]

(a) \[[\mathbf{a}+\mathbf{b}\,\,\,\mathbf{b}+\mathbf{c}\,\,\,\mathbf{c}+\mathbf{a}]=2[\mathbf{a}\,\,\mathbf{b}\,\,\mathbf{c}]\]  

(b) \[[\mathbf{a}-\mathbf{b}\,\,\,\mathbf{b}-\mathbf{c}\,\,\,\mathbf{c}-\mathbf{a}]=0\]  

(c) \[[\mathbf{a}\times \mathbf{b}\,\,\,\mathbf{b}\times \mathbf{c}\,\,\,\mathbf{c}\times \mathbf{a}]={{[\mathbf{a}\,\,\mathbf{b}\,\,\mathbf{c}]}^{2}}\]

(4) Tetrahedron : A tetrahedron is a three-dimensional figure formed by four triangle \[OABC\] is a tetrahedron with \[\Delta ABC\] as the base. \[OA,\,OB,OC,AB,\,BC\] and \[CA\] are known as edges of the tetrahedron. \[OA,\,BC;\,OB,\,CA\] and \[OC,\,AB\] are known as the pairs of opposite edges. A tetrahedron in which all edges are equal, is called a regular tetrahedron. Any two edges of regular tetrahedron are perpendicular to each other.

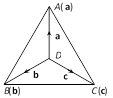
Volume of tetrahedron

(i) The volume of a tetrahedron  \[=\frac{1}{3}(\text{area of the base) (corresponding altitude)}\]\[=\frac{1}{6}[\overrightarrow{AB}\,\text{ }\overrightarrow{BC}\,\text{ }\overrightarrow{AD}]\]

(ii) If \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] are position vectors of vertices \[A,\,\,B\] and \[C\] with respect to \[O,\] then volume of tetrahedron \[OABC=\frac{1}{6}\,[\mathbf{a}\,\,\mathbf{b}\ \,\mathbf{c}]\].

(iii) If \[\mathbf{a},\,\mathbf{b},\,\mathbf{c},\,\mathbf{d}\] are position vectors of vertices \[A,B,C,D\] of a tetrahedron \[ABCD,\] then its volume \[=\frac{1}{6}[\mathbf{b}-\mathbf{a}\,\,\mathbf{c}-\mathbf{a}\,\,\mathbf{d}-\mathbf{a}]\].

(5) Reciprocal system of vectors : Let \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] be three non-coplanar vectors, and let\[\mathbf{{a}'}=\frac{\mathbf{b}\times \mathbf{c}}{[\mathbf{abc}]},\,\ \,\mathbf{{b}'}=\frac{\mathbf{c}\times \mathbf{a}}{[\mathbf{abc}]},\ \mathbf{{c}'}=\frac{\mathbf{a}\times \mathbf{b}}{[\mathbf{abc}]}\]. \[\mathbf{{a}',}\,\mathbf{{b}',}\,\mathbf{{c}'}\] are said to form a reciprocal system of vectors for the vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\].

If \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] and \[\mathbf{{a}'},\,\mathbf{{b}'},\,\mathbf{{c}'}\] form a reciprocal system of vectors, then

(i)   \[\mathbf{a}\,.\,\mathbf{{a}'}=\mathbf{b}\,.\,\mathbf{{b}'}=\mathbf{c}\,.\,\mathbf{{c}'}=1\]               

(ii)  \[\mathbf{a}\,.\,\mathbf{{b}'}=\mathbf{a}\,.\,\mathbf{{c}'}=0;\,\mathbf{b}\,.\,\mathbf{{c}'}=\mathbf{b}\,.\,\mathbf{{a}'}=0;\,\mathbf{c}\,.\,\mathbf{{a}'}=\mathbf{c}\,.\,\mathbf{{b}'}=0\]

(iii) \[[\mathbf{{a}'}\,\mathbf{{b}'}\,\mathbf{{c}'}]=\frac{1}{[\mathbf{a}\,\,\mathbf{b}\,\,\mathbf{c}]}\]

(iv)  \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] are non-coplanar iff so are \[\mathbf{{a}'},\,\mathbf{{b}'},\,\mathbf{{c}'}\].