Mechanics
Category : Banking
Introduction
Those quantities which can describe the laws of physics and possible to measure are called physical quantities. The physical quantities which do not depend upon other physical quantities are called fundamental quantities. In Standard International (S.I.) system the fundamental quantities are mass, length, time, temperature, luminous intensity, electric current and amount of substance. The physical quantities which depend on fundamental quantities are called derived quantities e.g. speed, acceleration, force, etc.
The unit of a physical quantity is the reference standard used to measure it.
Types of Units
The units defined for the fundamental quantities are called fundamental or base units.
|
Fundamental Physical quantity |
Mass (M) |
Length (L) |
Time (T) |
Temperature (\[\theta \]or k) |
Electric current (I) |
Luminous intensity |
Amount of Substance |
|
Fundamental unit |
Kilogram (kg) |
Meter (m) |
Second (s) |
Kelvin (k) |
Ampere (A) |
Candela (cd) |
Mole (mol) |
The units defined for the derived quantities are called derived units, e.g. unit of speed or velocity (metre per second),
Acceleration (metre per second\[\sec on{{d}^{2}}\]) etc.
Dimensions
|
S. No. |
Physical Quantity |
Formula |
Dimensional Formula |
SI Unit |
|
1. |
Area |
\[length\times breadth\] |
\[L\times L={{L}^{2}}={{M}^{0}}{{L}^{2}}{{T}^{0}}\] |
\[{{M}^{2}}\] |
|
2. |
Volume |
\[length\times breadth\times height\] |
\[L\times L\times L={{L}^{3}}={{M}^{0}}{{L}^{3}}{{T}^{0}}\] |
\[{{M}^{3}}\] |
|
3. |
Density |
Mass/volume |
\[{}^{M}/{}_{{{L}^{3}}}=M{{L}^{-3}}{{T}^{0}}\] |
\[kg/{{M}^{3}}\] |
|
4 |
Speed or velocity |
Distance/time |
\[{}^{L}/{}_{T}={{M}^{0}}L{{T}^{-1}}\] |
m/s |
|
5. |
Linear momentum |
\[mass\times velocity\] |
\[ML{{T}^{-1}}\] |
Kg m/s |
|
6. |
Acceleration |
\[\frac{changeinvelocity}{time}\] |
\[\frac{L{{T}^{-1}}}{T}={{M}^{0}}L{{T}^{-2}}\] |
\[m/{{s}^{2}}\] |
|
7. |
Force |
\[mass\times acceleration\] |
\[ML{{T}^{-2}}\] |
Newton (N) |
|
8. |
Impulse |
\[Force\times time\] |
\[ML{{T}^{-2}}\times T=ML{{T}^{-1}}\] |
Ns |
|
9. |
Pressure |
Force/area |
\[ML{{T}^{-2}}/{{L}^{2}}=M{{L}^{-1}}{{T}^{-2}}\] |
\[N/{{m}^{2}}\] |
|
10. |
Work |
\[force\times displacement\] |
\[ML{{T}^{-2}}\times L=M{{L}^{2}}{{T}^{-2}}\] |
Joule (j) |
|
11. |
Energy |
\[mghor\frac{1}{2}m{{v}^{2}}\] |
\[M{{L}^{2}}{{T}^{-2}}\] |
J |
|
12. |
Power |
Work/time |
\[M{{L}^{2}}{{T}^{-2}}/T=M{{L}^{2}}{{T}^{-2}}\] |
Watt (W) |
|
13. |
Moment of force |
\[Force\times dis\tan ce\] |
\[ML{{T}^{-2}}\times L=M{{L}^{2}}{{T}^{-2}}\] |
N-m |
|
14. |
Universal gravitational constant |
\[G=\frac{f{{r}^{2}}}{{{m}_{1}}{{m}_{2}}}\] |
\[G=\frac{ML{{T}^{-2}}\times {{L}^{2}}}{{{M}^{2}}}={{M}^{-1}}{{L}^{3}}{{T}^{-2}}\] |
\[N{{m}^{2}}/K{{g}^{2}}\] |
|
15. |
Surface tension |
Force/length |
\[ML{{T}^{-2}}/L=M{{L}^{0}}{{T}^{-2}}\] |
N/m |
|
16. |
Surface energy |
Energy/area |
\[M{{L}^{2}}{{T}^{-2}}/{{L}^{2}}=M{{L}^{0}}{{T}^{-2}}\] |
\[J/{{M}^{2}}\] |
|
17. |
Thrust, tension |
Force |
\[ML{{T}^{-2}}\] |
Newton(N) |
|
18. |
Stress |
Force /area |
\[ML{{T}^{-2}}/{{L}^{2}}=M{{L}^{-1}}{{T}^{-2}}\] |
\[N/{{M}^{2}}\] |
|
19. |
Strain |
\[\frac{change\,in\,configuratrion}{inital\,configuration}\] |
\[{{M}^{0}}{{L}^{0}}{{T}^{0}}\]( dimensionless) |
No unit |
|
20. |
Modulus of elasticity |
Stress/strain |
\[M{{L}^{-1}}{{T}^{-2}}\] |
\[N/{{m}^{2}}\] |
|
21. |
Radius of gyration |
Length |
\[{{M}^{0}}L{{T}^{0}}\] |
M |
|
22. |
Moment of inertia |
\[Mass\times {{(dis\tan ce)}^{2}}\] |
\[M{{L}^{2}}{{T}^{0}}\] |
\[kg{{m}^{2}}\] |
|
23. |
Angle |
Length /radius |
\[{{M}^{0}}{{L}^{0}}{{T}^{0}}\] |
Radian |
|
24. |
Angular velocity |
\[\frac{angular\,displacement}{time}\] |
\[\frac{1}{T}={{M}^{0}}{{L}^{0}}{{T}^{-1}}\] |
Rad/s |
|
25. |
Angular acceleration |
\[\frac{angular\,velocity}{time}\] |
\[\frac{{{M}^{0}}{{L}^{0}}{{T}^{-1}}}{T}={{M}^{0}}{{L}^{0}}{{T}^{-2}}\] |
\[rad/{{s}^{2}}\] |
|
26. |
Angular momentum |
Moment of inertia \[\times \] angular velocity |
\[M{{L}^{2}}{{T}^{-1}}\] |
\[kg\,{{m}^{2}}/s\] |
|
27. |
Torque |
Moment of inertia \[\times \]angular acceleration |
\[M{{L}^{2}}{{T}^{-2}}\] |
N-m |
|
28. |
Wavelength |
Length |
\[{{M}^{0}}L{{T}^{0}}\] |
M |
|
29. |
Frequency |
No. of vibrations/s |
\[\frac{1}{T}={{M}^{0}}{{L}^{0}}{{T}^{-1}}\] |
\[{{S}^{-1}}\] |
|
30. |
Velocity gradient |
Velocity/distance |
\[\frac{L{{T}^{-1}}}{L}={{M}^{0}}{{L}^{0}}{{T}^{-1}}\] |
\[{{s}^{-1}}\] |
Rounding Off
The preceding digit is raised by 1 if the uncertain digit to be dropped is more than 5 and is left unchanged if the latter is less than 5.
Example: x = 5.686 is rounded off to 5.69 (as 6 > 5) x = 3.462 is rounded off to 3.46 (as 2 < 5)
If the uncertain digit to be dropped is 5, the preceeding digit raised by 1 if it is odd and is left unchanged if it is even digit.
Example: 7.735 is rounded off to three significant figures becomes 7.74 as proceeding digit is odd.
7.745 is rounded off to 7.74 as preceeding digit is even.
The length of the actual path between initial and final positions of a particle in a given interval of time is called distance covered by the particle. Displacement The shortest distance from the initial position to the final position of the particle is called displacement.
Comparative Study of Displacement and distance
|
S. No |
Displacement |
Distance |
|
1. |
It has single value between two points. |
It may have more than one value between two points. |
|
2. |
May be +ive, -ive or zero. |
It is always > 0 (+ive) |
|
3. |
It can decrease with time. |
It can never decrease with time |
|
4.` |
It is a vector quantity |
It is a scalar quantity. |
\[\text{speed}\,\text{=}\,\,\frac{\text{Distance}\,\text{travelled}}{\text{time}\,\text{taken}}\],
\[\text{Average}\,\,\text{speed}\,\overline{\text{V}}\,\text{=}\,\,\frac{\text{Total}\,\text{distance}\,\text{travelled}}{\text{Total}\,\text{time}\,\text{taken}}\],
Instantaneous speed= \[\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta x}{\Delta t}=\frac{dx}{dt}\]
\[\text{Velocity}\,\,\text{=}\,\,\frac{\text{displacement}}{\text{Time}\,\text{interval}}\]
\[\text{Average}\,\text{velocity}\,\text{=}\,\frac{\text{Displacement}}{\text{Total}\,\text{time}\,\text{taken}}\]
\[\text{Instantaneous}\,\,\text{velocity}\overrightarrow{\,\,V}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta \overrightarrow{x}}{dt}=\frac{d\overrightarrow{x}}{dt}\]
Acceleration\[(\overrightarrow{a)}=\frac{change\,in\,velocity}{Time\,\operatorname{int}erval}=\frac{\overrightarrow{v'}-\overrightarrow{v}}{t'-t}\]average,
Acceleration\[=\frac{Total\,change\,in\,velocity}{Total\,time\,taken}\],
\[{{\overrightarrow{a}}_{inst}}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta \overrightarrow{v}}{\Delta t}=\frac{\overrightarrow{dv}}{dt}\]
Motion under uniform acceleration is described by the following equations.
\[V=u+at;\]\[s=ut+\frac{1}{2}a{{t}^{2}}\] and \[{{v}^{2}}={{u}^{2}}+2as\]
\[{{S}_{{{n}^{th}}}}={{S}_{n}}-{{S}_{n-1}}=(un+\frac{1}{2}a{{n}^{2}})-[u(n-1)+\frac{1}{2}a{{(n-1)}^{2}}]\]
So, \[{{S}_{{{n}^{th}}}}=u+\frac{a}{2}(2n-1)\]
If \[\overrightarrow{{{v}_{A}}}\]and \[\overrightarrow{{{v}_{B}}}\] be the respective velocities of object A and B then relative velocity of A w.r.t B is
\[{{\overrightarrow{V}}_{AB}}={{\overrightarrow{V}}_{A}}-{{\overrightarrow{V}}_{B}}\]
Similarly, relative velocity of B w.r.t. A is\[{{\overrightarrow{V}}_{BA}}={{\overrightarrow{V}}_{B}}-{{\overrightarrow{V}}_{A}}\]
The physical quantities which require only magnitude to express, are called scalar quantities. Ex. Mass, distance, time, speed, volume, density, pressure, work, energy, power, charge, electric current, temperature, potential, specific Beat, frequency, etc. Certain physical quantities have both magnitude and direction, they are called vector quantities. Ex. Displacement, velocity, acceleration, force, momentum, impulse, electric field, magnetic field, current density, etc.
Cross product of \[\overrightarrow{A}\] and \[\overrightarrow{B}\] inclined to each other at an angle \[\theta \] is defined as:
\[AB\,\sin \theta \,\hat{n}=\overrightarrow{A}\times \overrightarrow{B}\]
\[\hat{n}\bot \,toplane\,of\,\overrightarrow{A}\,and\,\overrightarrow{B}\]
The vector product of unit orthogonal vectors \[\hat{i}\]\[\hat{j}\] and \[\hat{k}\] have the following relations in the right-handed coordinate system.
(a) \[\hat{i}\times \hat{j}=\hat{k}\] \[\hat{j}\times \hat{i}=-\hat{k}\]
\[\hat{j}\times \hat{k}=\hat{i}\] \[\hat{K}\times \hat{j}=-\hat{i}\]
\[\hat{k}\times \hat{i}=0\] \[\hat{i}\times \hat{k}=-\hat{j}\]
(b) \[\hat{i}\times \hat{i}=0\] \[\hat{j}\times \hat{j}=0\] \[\hat{k}\times \hat{k}=0\]
If \[\theta \] is the angle between \[\overrightarrow{A}\] and \[\overrightarrow{B}\]. Then A (B cos \[\theta \]) = \[\overrightarrow{A}\]•\[\overrightarrow{B}\] , A and B are the magnitudes of vectors \[\overrightarrow{A}\] and \[\overrightarrow{B}\] .
\[\hat{i}\bullet \hat{j}=0\],\[\hat{j}\,\centerdot \,\hat{k}=0,\hat{k}\,\centerdot \,\hat{i}=0\],
\[\hat{i}\,\centerdot \,\hat{i}=1,\,\,\hat{j}\,\centerdot \,\hat{j}=1,\,\,\hat{k}\,\centerdot \,\hat{k}=1\]
1st law: Every-body continues to be in its state of rest or of uniform motion in a straight line unless compelled by an external force to change its state. This fundamental property of the body is called inertia. This law is known as Newton’s first law of motion or law of inertia.
Inertia is the property of a body due to 'which it opposes the change in its state. Inertia of a body is measured by mass of the body It is directly proportional to the mass of the body i.e., Inertia \[\propto \]mass.
Momentum
The linear momentum of a body (p) is defined as the product of the mass of the body (m) and its velocity (v) .i.e.,\[\overrightarrow{p}=m\overrightarrow{v}\]
Consider a body of mass m moving with velocity v. Linear momentum of the body, p = mv. KE of a particle can be expressed as\[E=\frac{{{p}^{2}}}{2m}\]and\[p=\sqrt{2mE}\]
2nd law: The rate of change of momentum of a body is directly proportional to the unbalanced external force applied on it.
\[\overrightarrow{f}\propto \frac{d\overrightarrow{p}}{dt}\]or, \[\overrightarrow{f}=k\frac{d\overrightarrow{p}}{dt}\], or \[\overrightarrow{F}=m\overrightarrow{a}\]
If a large force acts on a body or particle for a smaller time, then impulse =product of force and time.
Impulse\[=\overrightarrow{F}\Delta t\]
3rd law: According to this law, every action has equal and opposite reaction. Action and reaction act on two different bodies and they are simultaneous. There can be no reaction without action.
If the total external force acting on a system is equal to zero, then the final value of the total momentum of the system is equal to the initial value of the total momentum of the system.
\[\overrightarrow{p}\]= constant or \[={{\overrightarrow{p}}_{f}}\] = \[{{\overrightarrow{p}}_{i}}\]
Let a man of weight W = Mg be standing in a lift.
Case (a): If the lift is moving with constant velocity v upwards or downwards. In this case there is no accelerated motion hence no pseudo force experienced by observer '0' inside the lift. So apparent weight, W = actual weight W.
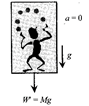
Case (b): If the lift is accelerated i.e., a = constant and in upward direction.
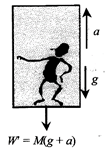
Then net forces acting on the man are
(i) weight W= Mg downward
(ii) fictitious force \[{{F}_{0}}=Ma\]downward.
So apparent weight,
\[W'=W+{{F}_{0}}=Mg+Ma=M(g+a)\]
Case (c): If the lift is accelerated downward with acceleration a<g:
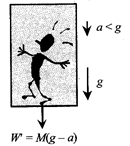
The fictitious force \[{{F}_{0}}=Ma\]acts upward while weight of a man \[W'=Mg\]always acts downward, therefor apparent weight \[W'=W+{{F}_{0}}=Mg-Ma=M(g-a)\],
Friction
Whenever a body moves or tends to move over the surface of another body, a force comes into play which acts parallel to the surface of contact and opposes the relative motion. This opposing force is called friction.
(i) It depends on the nature of the surfaces in contact and their state of polish.
(ii) It acts tangential to the two surfaces in contact and in a direction opposite to the direction of motion of the body.
(iii) The value of limiting friction is independent of the area of the surface in contact so long as the normal reaction remains the same.
(iv) The limiting friction (\[{{F}_{s}}\]max) is directly proportional to the normal reaction R between the two surfaces. i.e \[{{f}_{s}}\max \propto R\] or \[{{f}_{s}}\max \propto {{\mu }_{s}}R\] or \[{{\mu }_{s}}=\frac{{{f}_{s}}\max }{R}=\frac{Limiting\,fricition}{Normal\,reaction}\]
The force directed towards the centre required for traversing a circular path is called centripetal force.
Centripetal force = \[F=\frac{{{M}^{2}}}{r}=m{{\omega }^{2}}r\] .
Bending of cyclist: In order to take a circular turn of radius r with speed v, the cyclist should bend himself through an angle \[\theta \] from the vertical such that \[\tan \theta =\frac{{{V}^{2}}}{rg}\]
Work
Work done (W) by a constant force (\[\overrightarrow{F}\]) producing a displacement (\[\overrightarrow{S}\]) is \[W=\overrightarrow{F}.\overrightarrow{S}=FS\cos \theta \] where \[\theta \] is the angle between \[\overrightarrow{F}\] and \[\overrightarrow{S}\].
Work done by a variable force =\[\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{Fdx,}\]where F=F(x) and \[{{x}_{1}}\] and \[{{x}_{2}}\] are initial and final positions.
Work done by a stretched spring = W=\[\int{kxdx=\frac{1}{2}k{{x}^{2}}}\].
Power
Where k is spring constant.
Power is the rate of doing work.
Power=\[p=\frac{dw}{dt}=\frac{\overrightarrow{F}.d\,\overrightarrow{S}}{dt}=\overrightarrow{F}.\overrightarrow{V}\]\[=Fv\cos \theta \left[ \because \,\,\,\overrightarrow{V}=\frac{d\overrightarrow{s}}{dt} \right]\]where 9 is the angle between \[\overrightarrow{F}\] and \[\overrightarrow{v}\]. Its SI unit is watt.
1 Horse power [1HP] = 746 W, 1 calorie = 4.2J and 1 kW h \[=3.6\times {{10}^{6}}J\]
Energy is the capacity of doing work. It is also a scalar quantity. The SI unit is joule. Work-energy theorem states that the work done on a body is equal to the change in its kinetic energy.
Collision
Elastic collision: Both momentum and K.E. are conserved. For elastic collision in one dimension.
Inelastic collision: Only momentum is conserved. Coefficient of restitution is defined as the ratio of velocity of separation to the velocity of approach. Coefficient of restitution = \[e=\frac{{{v}_{2}}-{{v}_{1}}}{{{u}_{1}}-{{u}_{2}}}\] e= 1 for perfectly elastic collision e = 0 for perfectly inelastic collision
Centre of Mass
It is an imaginary point at which the whole mass of a body is supposed to be concentrated.
(i) It need not hold mass physically, e.g. for a hollow sphere, center of mass is at the geometrical centre of the sphere although there is no mass present physically at the centre.
(ii) Location of centre of mass depends on the distribution of masses and their individual location. For regular geometrical shaped bodies, having uniform distribution of mass, the centre of mass is located at their centres.
(iii) When no external force acts on a body, centre of mass ha constant velocity and constant angular momentum. Acceleration is zero. If C.M. is the origin, then \[\sum\limits_{i=1}^{n}{Mi{{\overrightarrow{r}}_{i}}=0}\]
Torque is the moment offeree. It is the cross product of the force with the perpendicular distance between the axis of rotation and the point of application of force with the force. Torque \[=\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F}\]S.I. unit is N - m
Angular momentum is the moment of linear momentum. It is also the product of the linear momentum and the perpendicular distance of the mass from the axis of rotation. \[=\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{p}\] where \[\overrightarrow{r}\] = position relative to origin \[\overrightarrow{p}\]= linear momentum at position. Angular momentum = L =\[\overrightarrow{r}\times \overrightarrow{p}\]: S.I unit kg \[{{m}^{2}}/s\] Relation between torque and angular momentum, \[=\overrightarrow{\tau }=\frac{d\overrightarrow{L}}{dt}\]
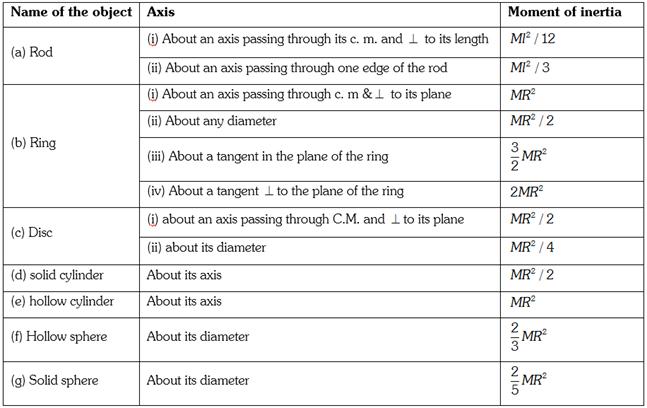
Moment of Inertia
It is equivalent to mass in rotational motion. It is defined as the sum of the product of the constituent masses and the square of their perpendicular distances from the axis of rotation. For an n-particle system having mass points \[{{m}_{1}},{{m}_{2}},{{m}_{3}}\]................ \[{{m}_{n}}\]at perpendicular distances \[{{r}_{1}},{{r}_{2}}\]............. \[{{r}_{n}}\] moment of inertia.
\[I={{m}_{1}}r_{1}^{2}+{{m}_{2}}r_{2}^{2}+.......+{{m}_{n}}r_{n}^{2}=\sum\limits_{i=1}^{n}{{{m}_{i}}r_{i}^{2}}\] S.I. unit is \[kg{{m}^{2}}\] and it is a scalar quantity.
It is the root mean square of the perpendicular distances of the constituent masses. It is the perpendicular distance of the point where the whole mass is concentrated form the axis of rotation.
Radius of gyration =\[k=\sqrt{\frac{r_{1}^{2}+r_{2}^{2}+....+r_{n}^{2}}{n}}\]
Moment of inertia \[I=M{{k}^{2}}\]
Gravitation
It is the force of attraction between any two bodies.
\[F\propto {{m}_{1}}{{m}_{2}}\] and \[F\propto \frac{1}{{{r}^{2}}}\Rightarrow F\propto \frac{{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\]
\[\therefore F=G\frac{{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\] G = Universal gravitational constant \[=6.67\times {{10}^{-11}}N{{m}^{2}}/k{{g}^{2}}\]
\[{{M}_{e}}=\frac{gR_{e}^{2}}{G}=6\times {{10}^{24}}Kg,\]\[{{\operatorname{R}}_{e}}\] = 6400 km;
Density = \[\rho =\frac{3g}{4\pi {{\operatorname{R}}_{e}}G}=5.5\times {{10}^{3}}Kg/{{m}^{3}}\]
(a) With height: g' \[=g\left( 1-\frac{2h}{R} \right)\] when h << R, \[g'=g{{\left( \frac{R}{R+h} \right)}^{2}}\]when \[h\approx R\]\[\therefore g\,\]decreases with height.
(b) With depth: g' \[=g\left( 1-\frac{d}{R} \right)\]\[\therefore g\] decreases with depth. At the centre of the earth d = R, g' = 0
(c) Effect of latitude:
\[g'=g-R{{\omega }^{2}}{{\cos }^{2}}\theta \]
where \[\theta \to \] latitude of the point
\[\omega \to \] angular velocity of the earth.
(d) Effect of the shape of the earth:
The equatorial radius is 21 km (approx) greater than the polar radius.
\[\because g\propto \frac{1}{{{R}^{2}}}\]
\[\therefore g\] Increases from equator to poles. i.e., g is maximum at poles and least (zero) at equator.
Gravitational potential at a point in a gravitational field is defined as the work done in taking a unit mass from infinity to the point.
Gravitational potential \[=\frac{-GM}{r}\]
Gravitational P.E. = Gravitational potential \[\times \] mass of the object \[=-\frac{GMm}{r}\]
Minimum speed required to escape the earth's gravitational pull. \[{{v}_{e}}=\sqrt{2gR}=\sqrt{2}\times {{v}_{0}}\](For earth \[{{v}_{e}}\]=11.2 Km/s) where \[{{v}_{0}}\]= Oribital speed
It is a heavenly body or an artificial object which revolves round a planet in a particular orbit. The required centripetal force is provided by the gravitational force. Kepler's laws of planetary motion are applicable to them.
(a) Orbital velocity of a satellite: Velocity with which the satellite orbits around the planet.
\[{{v}_{0}}=\sqrt{\frac{GM}{R+h}}\]
\[h\to \] height of the orbit from the surface of the planet;
\[R\to \] Radius of the planet.
If h<<R \[{{V}_{0}}=\sqrt{\frac{GM}{R}}=\sqrt{gR}\]
(b) Time period of a satellite: Time taken by it to complete one revolution around the planet.
\[T=\sqrt{\frac{3\pi {{(R+h)}^{3}}}{G\rho {{R}^{3}}}}=\frac{2\pi }{R}\sqrt{\frac{{{(R+h)}^{3}}}{g}}\] where \[\rho \to \] mean density of the planet;
For h<<R; \[T=\sqrt{\frac{3\pi }{G\rho }}\]
(c) Height of a satellite above the surface of the planet: \[H={{\left( \frac{{{T}^{2}}{{R}^{2}}g}{4{{\pi }^{2}}} \right)}^{1/3}}-R\]
(d) "Total energy of a satellite orbiting on a circular path is negative" with potential energy being negative but twice as the magnitude of positive kinetic energy.
(e) Binding energy of a satellite is the energy required to remove it from its orbit to infinity.
\[B.E=\frac{GMm}{2r}\] No energy is required to keep the satellite in its orbit.
Polar Satellites: A satellite that revolves in a polar orbit along north-south direction while the earth rotates around its axis in east west direction.
A situation where the effective weight of the object becomes zero. An astronaut experiences weightlessness in space satellite because the astronaut as well as the satellite are in a free fall state towards the earth.
You need to login to perform this action.
You will be redirected in
3 sec
