8th Class Mathematics Rational Numbers

RATIONAL NUMBERS

 

FUNDAMENTALS

Rational Number:-

• A number which can be expressed as\[\frac{x}{y}\], where x and y are Integers and \[y\ne 0\] is called a rational number.

e.g., \[\frac{1}{2},\frac{2}{2},\frac{-1}{2},0,\frac{3}{-\,2}\] etc.

• Set of rational number is denoted by Z.
• A Rational number may be positive, zero or negative
• If \[\frac{x}{y}\] is a rational number and \[\frac{x}{y}>0\], then\[\frac{x}{y}\] is called a positive Rational Number.

e.g., \[\frac{1}{2},\frac{2}{5},\frac{-3}{-2},-\left( -\frac{1}{2} \right)\]etc.

 

Negative Rational Numbers:-

• If \[\frac{x}{y}\] is a rational number and \[\frac{x}{y}<0\], then \[\frac{x}{y}\]is called a Negative Rational Number.

e.g., \[\frac{-1}{2}.\frac{3}{-2},\frac{-7}{11}......\]etc.

 

Standard form of Rational Number:-

• A Rational number \[\frac{x}{y}\] is said to be m standard form, if x and y are integers having no common divisor other than one, where \[y\ne 0\].

            e.g., \[\frac{-1}{2},\frac{5}{6},\frac{8}{11}\]……etc.

Note:- There are infinite rational numbers between any two rational numbers.

 

Property of Rational Number

• Let x and y are two rational number and y > x, then the rational number between x and y is\[\frac{1}{2}\left( x+y \right).\]

e.g., find 2 rational number between \[\frac{1}{3}\]and \[\frac{1}{2}\]

Solution:- Let \[x=\frac{1}{3}\] and \[y=\frac{1}{3}\] and y > x.

Then, Rational no. between\[\frac{1}{3}\]and\[\frac{1}{2}\]is

\[\frac{1}{2}\left( \frac{1}{3}+\frac{1}{2} \right)=\frac{1}{2}\left( \frac{2+3}{6} \right)=\frac{5}{12}\]

Again Let \[x=\frac{5}{12}\] and \[y=\frac{1}{2}\]  and y > x. then

Rational no. between \[\frac{5}{12}\] and \[\frac{1}{2}\] is

\[\frac{1}{2}\left( \frac{5}{12}+\frac{1}{2} \right)=\frac{1}{2}\left( \frac{5+6}{12} \right)=\frac{1}{2}\times \frac{11}{12}=\frac{11}{24}\]

Hence the Rational Numbers between \[\frac{1}{3}\] and \[\frac{1}{2}\] are \[\frac{5}{12}\] and \[\frac{11}{24}\].

• Let x and y are two rational number and y > x. Consider to find n rational numbers between x and y. Let d = \[\frac{y-x}{n+1}\]

Then 'n' rational number lying between x and y are \[\left( x+d \right),\left( x+2d \right),\left( x+3d \right),\_\_\_\left( x+nd \right).\]

Example:- Find 9 rational number between 2 and 3.

Solution:- Let x = 2 and y = 3 then y > x

Now \[\mathbf{d}=\frac{y-x}{n+1}=\frac{3-2}{9+1}=\frac{1}{10}\]

Then, rational number are, 2 + 0.1, 2 + 0.2, 2 + 0.3, 2 + 0.4, 2 + 0.5, 2 + 0.6, 2 + 0.7, 2 + 0.8, 2 + 0.9 = 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8 and 2.9.

 

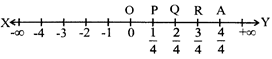
Representation of Rational Number on the Number line

• To represent - on the number line first we draw a number line

Let O represent 0 (zero) and A represent 1. So divide OA into 4 equal parts, each point in the middle representing P, Q and R. Point R represent\[\frac{3}{4}\].

 

 

Operations on Rational Numbers

• Addition of Rational Numbers:

Example: Find the sum of the rational numbers \[\frac{-4}{9},\frac{15}{12}\] and \[\frac{-7}{18}\].

Solution: \[\frac{-4}{9}+\frac{15}{12}+\frac{-7}{18}=\frac{-16+45-14}{36}=\frac{15}{36}=\frac{5}{12}\]

Properties of Addition of Rational Number

• Closure Property:- If a and b are two rational numbers, then a + b is always a rational number.

E.g., Let \[a=3\], \[b=-2,\] then \[a+b=3+\left( -2 \right)-1\]

• Commutative Property:- If a and b are two rational number then a + b = b + a.

E.g., Let \[a=\frac{1}{2}\]and \[b=\frac{1}{3}\] then

To check whether, a + b = b + a

\[\Rightarrow \frac{1}{2}+=\frac{1}{3}+\frac{1}{2}\]

\[\Rightarrow \frac{5}{6}=\frac{5}{6}\]

 

• Associative Property:-If a, b and c are three Rational number then, \[a+\left( b+c \right)=\left( a+b \right)+c.\]

E.g., \[a=1,\]\[b=-\,2\] and \[c=3\] then,

\[1+\left( -2+3 \right)=\left( 1-2 \right)+3\]

\[1+1=-1+3\]

2 = 2

 

Existence of additive identity (property of zero):-

• Zero is the additive identity for any Rational Number because when zero is added to any Rational Number, then sum is the same given Number, (a + 0 = a).

E.g., \[2+0=2,\,-2+0=-2,\,\,3+0=3,\,\,\frac{-1}{2}+0=\frac{-1}{2}\]

Existence of additive inverse;-

• Negative of rational number.

For\[\frac{a}{b}\], it is\[-\frac{a}{b}\]

e.g., For\[\frac{1}{2}\], it is\[-\frac{1}{2}\]

(\[-\frac{1}{2}\]is a additive inverse of\[\frac{1}{2}\])

\[-\frac{3}{2}\Rightarrow \frac{3}{2}\]  (\[\frac{3}{2}\] is a additive inverse of \[-\frac{3}{2}\])

Note:- Additive inverse of the rational number ‘0’ is 0 itself.

Subtraction of Rational Number:-

• Subtraction is inverse process of addition

If \[\frac{p}{q}\]and \[\frac{r}{s}\] be two rational number it follows  \[\frac{r}{s}-\frac{p}{q}=\frac{r}{s}+\left( -\frac{p}{q} \right)\]

e.g., subtract \[\frac{-2}{7}\] from \[\frac{3}{4}\].

Solution:- \[\frac{3}{4}-\left( -\frac{2}{7} \right)=\frac{3}{4}+\frac{2}{7}=\frac{21+8}{28}=\frac{29}{28}\]

 

Multiplication of Rational Number;

• The product of two rational numbers =\[\frac{\text{The Product of the numerators}}{\text{Product of the denominators}}\]

If \[\frac{a}{b}\] and \[\frac{c}{d}\] are two rational numbers, then \[\frac{a}{b}\times \frac{c}{d}=\frac{a\times c}{b\times d}\]

Example:- Multiply \[\frac{-17}{30}\] by \[\frac{15}{-34}\]

Solution:- \[\frac{-17}{30}\times \frac{15}{34}=\frac{-17\times 15}{30\times -34}=\frac{1}{4}\]

 

Properties of multiplication of Rational Numbers:

• Closure Property:- If \[\frac{a}{b}\] and \[\frac{c}{d}\] are two rational numbers, then \[\left( \frac{a}{b}\times \frac{c}{d} \right)\] is also a Rational Number.

e.g., \[\frac{2}{3}\times \frac{3}{4}=\frac{2\times 3}{3\times 4}=\frac{1}{2}\]

• Commutative Property:- If \[\frac{a}{b}\] and \[\frac{c}{d}\]are two rational numbers, then \[\frac{a}{b}\times \frac{c}{d}=\frac{c}{d}\times \frac{a}{b}\]

e.g., \[\frac{2}{3}\times \frac{3}{4}=\frac{3}{4}\times \frac{2}{3}\Rightarrow \frac{6}{12}=\frac{6}{12}\]

\[\frac{1}{2}=\frac{1}{2}\]

• Associative Property:- If \[\frac{a}{b},\frac{c}{d}\] and \[\frac{e}{f}\] are three rational numbers, then \[\frac{a}{b}\times \left( \frac{c}{d}\times \frac{e}{f} \right)=\left( \frac{a}{b}\times \frac{c}{d} \right)\times \frac{e}{f}\]

e.g., \[\frac{1}{2}\times \left( \frac{2}{3}\times \frac{3}{4} \right)=\left( \frac{1}{2}\times \frac{2}{3} \right)\times \frac{3}{4}\]

\[\frac{6}{24}=\frac{6}{24}\]

 

• Existence of Multiplicative Identity:- One is the multiplicative identity for any rational number because when 1 is multiplied to any Rational Number, Product is Given Rational Number itself.

e.g., \[\left( \frac{p}{q}\times 1 \right)=\frac{p}{q}\], \[\left( \frac{3}{4}\times 1 \right)=\frac{3}{4}\], \[\left( \frac{-5}{2}\times 1 \right)=\frac{-5}{2}\]

 

• Existence of Multiplicative inverse:- for any non-zero rational number \[\frac{a}{b}\], there exist a unique rational \[\frac{b}{a}\] such that \[\left( \frac{a}{b}\times \frac{b}{a} \right)=1.\]

Hence, we say that \[\frac{a}{b},\frac{b}{a}\] are multiplicative inverse of each other

e.g., (i) \[\frac{2}{3}\times \frac{3}{2}=1\]

(ii) \[\left( \frac{-3}{4}\times \frac{-4}{3} \right)=\frac{12}{12}=1\]          

 

• Distribution of Multiplication over Addition:- for any three rational numbers \[\frac{a}{b},\frac{b}{a}\] and \[\frac{e}{f}\]

\[\frac{a}{b}\times \left( \frac{c}{d}\times \frac{e}{f} \right)=\left( \frac{a}{b}\times \frac{c}{d} \right)+\left( \frac{a}{b}\times \frac{e}{f} \right).\] This property is called distributive property for multiplication over addition.

e.g., \[\frac{1}{2}\times \left( \frac{2}{3}+\frac{3}{4} \right)=\frac{1}{2}\left( \frac{8+9}{12} \right)=\frac{1}{2}\times \frac{17}{12}=\frac{17}{24}\]

 

• Division of Rational Number:- If \[\frac{a}{b}\] is divided by \[\frac{c}{d}\], then \[\frac{a}{b}\] is the dividend, \[\frac{c}{d}\] is the divisor and \[\frac{a}{b}\div \frac{c}{d}=\frac{a}{b}\times \frac{d}{c}\]is the quotient.

Example:- \[\frac{14}{57}\div \frac{42}{19}=\frac{14}{57}\times \frac{19}{42}=\frac{14\times 19}{57\times 42}=\frac{1}{9}\]

 

• Decimal representation of Rational Numbers:- A rational number can be expressed as a terminating or non-terminating, recurring decimal.

For example:-

1. \[\frac{1}{2}=0.5,\frac{1}{4}=0.25,\frac{1}{5}=0.2\] etc. are rational numbers which are terminating decimals.
2. \[\frac{4}{3}=1.333.....=1.\overline{3},\frac{1}{6}=0.1666.....=0.1\overline{6},\] \[\frac{1}{7}=0.142857142857....=0.\overline{142857},etc\]

are non-terminating repeating decimals.

 

• If a rational number (\[\ne \] integer) can be expressed in the form \[\frac{p}{{{2}^{n}}\times {{5}^{m}}},\] where \[\mathbf{P}\in \mathbf{Z},n\in W\] and \[m\in W\], the rational number will be terminating decimal otherwise, rational number will be non-terminating recurring decimal.

For Example:

1. \[\frac{3}{10}=\frac{3}{{{2}^{1}}\times {{5}^{1}}},\] So, \[\frac{3}{10}\] is a terminating decimal.
2. \[\frac{7}{250}=\frac{7}{{{2}^{1}}\times {{5}^{3}}},\] So, \[\frac{7}{250}\] is a terminating decimal.
3. \[\frac{8}{75}=\frac{8}{{{5}^{2}}\times 3}\] is a non-terminating, recurring decimal.

 

• Non-terminating recurring decimal is also called periodic decimal.

Method of expressing recurring decimals as rational number:

• The recurring part of the non-terminating recurring decimal is called period and the number of digits in the recurring part is called periodicity.

Example:

1. \[\frac{1}{3}=0.\overline{3}\], period = 3, Periodicity = 1
2. \[\frac{7}{15}=0.4\overline{6}\], Period = 6, Periodicity = 1
3. \[\frac{5}{13}=0.\overline{384615},\] Period=384615, Periodicity = 6

We can express non-terminating recurring decimals in the form of rational numbers.

Example-1:- Let us write \[0.2\overline{45}\] in the form of rational number.

Solution:- Let x =\[0.2\overline{45}\]                 (i)

Then \[10x=2.4545\]..............                (ii)

Also, \[1000x=245.4545\]........... (iii)

On subtracting (ii) from (iii), we get: \[990x=245\Leftrightarrow x=\frac{245}{990}=\frac{49}{198}\].

Hence, \[0.2\overline{45}=\frac{40}{198}.\]

Example-2:- Let us find the rational form of\[0.\overline{428571}\].

Solution:- The periodicity of the recurring decimal is 6. So multiply the decimal fraction by 10⁶, \[0.\overline{428571}\] = x (say)

\[{{10}^{6}}=1000000\,x=428571.\overline{428571}\]

\[x=0.\overline{428571}\]

\[99999x=428571\]

 \[\therefore x=\frac{428571}{999999}=\frac{3}{7}\]

 

Example-3:- Express \[15.0\overline{2}\] as a rational Number

 

Solution:- Here, the whole number obtained by writing digits in there order =1502. The whole number made by the non-recurring digits in order = 150,

The number of digits after the decimal point = 2 (two)

The number of digits after the decimals point do not recur = one

\[\therefore 15.0\overline{2}=\frac{1502-150}{{{10}^{2}}-{{10}^{1}}}=\frac{1352}{90}=\frac{676}{45}\]