SYMMETRY

WHAT IS SYMMETRY?
- Mathematically, symmetry means that one shape becomes exactly like another when you move it in some way - turn (rotate), flip or slide.
- Line of symmetry: If a line divides a given figure into two coinciding parts, we say that the figure is symmetrical about the line and the line is called the axis of symmetry or line of symmetry.
For e.g.,

- A line of symmetry is also called a mirror line / mirror symmetry / reflection symmetry.
- A figure may have no line of symmetry, only one line of symmetry, two lines of symmetry or multiple lines of symmetry.
- Regular polygons have equal sides and equal angles. They have multiple lines of symmetry.
e.g.,
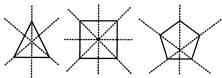
- Each regular polygon has as many lines of symmetry as its sides.
- A scalene triangle has no line of symmetry.
- A parallelogram in general has no line of symmetry. However if it is a parallelogram, which is either a square or a rectangle or a rhombus it will have line of symmetry.
- A line segment is symmetrical about its perpendicular bisector.
- An angle with equal arms has one line of symmetry.
- An isosceles triangle has one line of symmetry.
- An isosceles trapezium has one line of symmetry.
Elementary question-1: What are the properties of an isosceles trapezium? Show by drawing figure.
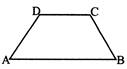
If ABCD is isosceles trapezium, then \[AB||CD\] and \[AD=BC;\] ABCD has one line of symmetry.
- A semicircle has one line of symmetry.
- A kite has one line of symmetry.
- A rectangle has two lines of symmetry.
- A rhombus has two lines of symmetry.
- An equilateral triangle has three lines of symmetry.
- A square has four lines of symmetry.
- A circle has an infinite number of lines of symmetry.
- In English alphabet, the letters A. B, C, D, E, K, M, T, U, V, W and Y have one line of symmetry and the letters H, I, X have two lines of symmetry.
- In English alphabet, the letters F, G, J, L, N, P, Q, R, S and Z have no line of symmetry.
The letter O has infinite lines of symmetry.
|
Letters of the English alphabet
|
|
A, M, T, U, V, W and Y
|
Vertical line of symmetry
|
|
B, C, D, E and K
|
Horizontal line of symmetry
|
|
H, I and X
|
Both vertical and horizontal lines of symmetry
|
|
F, G, J, L, N, P, Q, R, S, and Z
|
No line of symmetry
|
|
O
|
Infinitely many lines of symmetry like a circle
|
- The line symmetry is closely related to mirror reflection. In a plane mirror, there is isolateral inversion, i.e., the left right changes in orientation.
- Point symmetry: A figure is said to be symmetric about a point 0, called the centre of symmetry, if corresponding to each point P on the figure, there exists a point P' on the other side of the centre, which is exactly opposite to the point P and lies in the figure.
Note: A figure that possesses a point symmetry, regains its original shape even after being rotated through\[180{}^\circ \].
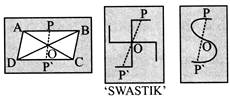
- Rotational symmetry: A figure is said to have rotational symmetry if it fits into itself more than once during a complete rotation.
- The number of times a figure fits onto itself in one complete rotation is called the order of rotational symmetry (r. s.).
- Swastik symbol as shown above has r.s. of order 2 about point O.
- A line segment AB possesses a rotational symmetry of order 2 about the midpoint O of the line segment. This is also called 2 fold symmetry.
- An equilateral triangle ABC possesses a rotational symmetry of order 3 about the point of intersection O of the bisectors of the interior angles. This is also called 3-fold symmetry.
Elementary question-2: A square possesses how many fold symmetry?
Ans. 4 - fold symmetry
- A rhombus ABCD possesses a rotational symmetry of order 2 about the point of intersection O of its diagonals.
- A rectangle ABCD possesses a rotational symmetry of order 2 about the point of intersection O of its diagonals.
- A parallelogram ABCD possesses a rotational symmetry of order 2 about the point of intersection O of its diagonals.
- A regular pentagon possesses a rotational symmetry of order 5 about the point of intersection O of the perpendicular bisectors of the sides of the pentagon.
- A regular hexagon possesses a rotational symmetry of order 6 about the centre O of the hexagon, i.e., for every rotation of \[\frac{360}{n}\,\,\,(n=6)\,=\frac{360}{6}=60{}^\circ ,\] it regains same configuration.
- A circle with centre O possesses a rotational symmetry of an infinite order about the centre O.
- The following letters of the English alphabet have rotational symmetry about the point marked on them.
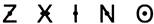





![]()
