Properties of Triangle
Category : 7th Class
PROPERTIES OF TRIANGLE
FUNDAMENTALS
Elementary Question -1
Identify triangle among following figures and also identify its six elements and vertices.
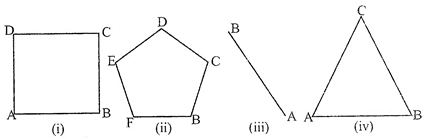
The figure (iv) is a triangle
Its sides are AB, BC, CA and angles are \[\angle A,\angle B,\angle C\] (also written as \[\angle BAC,\angle CBA\]and \[\angle ACB\]). These are six elements and its vertices are points A, B, C.
(a) An acute angled triangle, if each one of its angles measures less than \[90{}^\circ .\]
(b) A right angled triangle, if any one of its angles measures \[90{}^\circ .\]
(c) An obtuse angled triangle, if any one of its angles measures more than \[90{}^\circ .\]
Note: A triangle cannot have more than one right angle.
A triangle cannot have more than one obtuse angle.
In a right triangle, the sum of the acute angles is \[90{}^\circ .\]
This is such an important property that it will be used right from class VII to graduation level and even higher (post -graduation level). Hence it is very important, commit to memory, and apply wherever required.
(a) The sum of any two sides of a triangle is greater than the third side.
(b) The difference of any two sides is less than the third side.
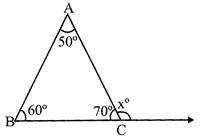
e.g., Exterior angle,
\[x{}^\circ =\angle A+\angle B=50{}^\circ +60{}^\circ =110{}^\circ \]
(a) An equilateral triangle, If all of its sides are equal.
(b) An isosceles triangle, if any two of its sides are equal.
(c) A scalene triangle, if all of its sides are of different lengths.
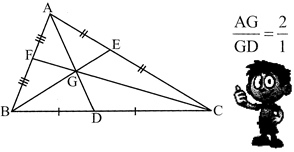
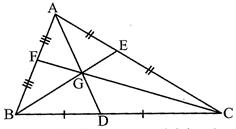
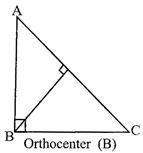
Important terms; Medians & centroid, altitudes & orthocenter:
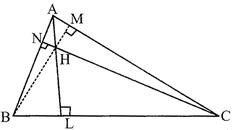
Here AL, BM and CN are the altitudes of \[\Delta ABC\].
Properties:
(a) The altitudes drawn on equal sides of an isosceles triangle are equal.
(b) The altitude bisects the base of an isosceles triangle.
(c) The altitudes of an equilateral triangle are equal.
(d) The centroid of an equilateral triangle coincides with its orthocenter.
Exercise for the students
You should practice each of these properties by drawing roughly appropriate Ale and drawing altitudes in them.
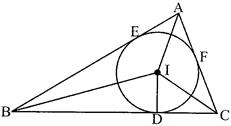
In center: Draw angle bisectors of a triangle as shown they meet at point 'I', called in centre.
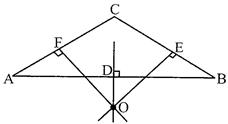
From I, draw a perpendicular to line BC so that \[ID\bot BC\]. Taking ID as radius we can draw an in circle DEF. Hence, it is called in centre and \[ID=IE=IF\] (where \[IE\bot AB,\,\,\,IF\bot AC\]) which are called radii?s of in circle.
Circumcentre: Draw perpendicular from midpoints D, E, F lying on sides AB, BC and CA respectively. Let them meet at 0, which is called circumcentre. This ensures that \[OA=OB=OE\] If we draw a circle with radius \[OA=OB=OC,\]then we get a circle touching vertices A, B and C of triangle. Hence, O is given the name -circum centre of \[\Delta ABC\] because it circumscribes \[\Delta ABC\].
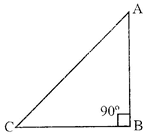
Properties of Right - angled
In the right angled triangle
\[ABC,\text{ }A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}.\]
You need to login to perform this action.
You will be redirected in
3 sec
