Mensuration
Category : 6th Class
Mensuration
Learning Objectives
Mensuration
Mensuration is the branch of mathematics which deals with the measurement of lengths, area and volume of the plane and solid figures.
Perimeter of a plane figure: The distance all round a plane figure is called perimeter of the figure or the lengths of boundary of a plane figure is known as its perimeter
\
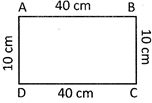
Perimeter of the quadrilateral \[ABCD=AB+BC+CD+DA\]
\[=40\text{ }cm+10\text{ }cm+40\text{ }cm+10\text{ }cm\]
\[=100\text{ }cm\]
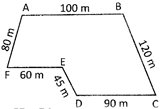
Perimeter of the hexagon \[ABCDEF=AB+BC+CD+DE+EF+FA\]
\[=100\text{ }m+120\text{ }m+90\text{ }m+45\text{ }m+60\text{ }m+80\text{ }m\]
\[=495\text{ }m\]
Perimeter of a scalene triangle = Sum of all the three sides of the triangle.
Example: Find the perimeter of the triangle ABC.
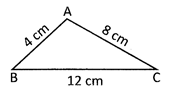
Perimeter of the triangle \[ABC=AB+BC+CA\]
\[=4\text{ }cm+12\text{ }cm+8\text{ }cm\]
\[=24cm\]
Perimeter of a rectangle \[=2\times \left( length+breadth \right).\]
Example: Find the perimeter of the following rectangle ABCD.
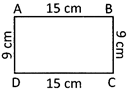
Perimeter of rectangle \[ABCD=2\times \left( AB+BC \right)\]
\[=2\times \left( 15cm+9cm \right)\]
\[=48\text{ }cm\]
Perimeter of regular shapes
Perimeter of an equilateral triangle \[\text{=3 }\!\!\times\!\!\text{ length of one side}\].
Example: Find the perimeter of the given triangle.
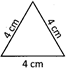
Perimeter of the triangle \[=3\times 4\text{ }cm\]
\[=12\text{ }cm\]
Perimeter of a square: \[\text{4 }\!\!\times\!\!\text{ length of one side}\text{.}\]
Example: Find the perimeter of the given square.
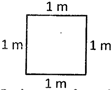
Perimeter of the square \[=4\times 1\text{ }m\]
\[=4\text{ }m\]
Perimeter of regular pentagon \[=5\text{ }\times \text{ }length\text{ }of\text{ }one\text{ }side.\]
Example: Find the perimeter of the given pentagon.
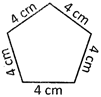
Perimeter of the pentagon \[=5\times 4\text{ }cm\]
\[=20\text{ }cm\]
Perimeter of the regular hexagon \[=6\times length\text{ }of\text{ }one\text{ }side.\]
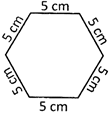
Perimeter of the hexagon \[=6\times 5\text{ }cm\]
\[=30\text{ }cm.\]
Area of a plane figure: The measurement of the region enclosed by a plane figure is called area of the figure or area is the amount of surface covered by the shape.
Area of triangle \[=\frac{1}{2}\times base\times height.\]
Example: Find the area of the given triangle.
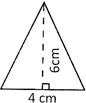
Area of the triangle \[=\frac{1}{2}\times 4cm\times 6cm=12c{{m}^{2}}\]
Area of rectangle: \[length\times breadth.\]
Example: Find the area of the given rectangle.
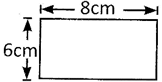
Area of the rectangle \[=8\text{ }cm\times 6\text{ }cm=48\text{ }c{{m}^{2}}\]
Area of square = \[side\times side\]
Example: Find the area of the given square.
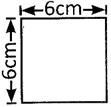
Area of the square \[=6cm\times 6cm=36c{{m}^{2}}.\]
Commonly Asked Questions
Find the area of a square park whose perimeter is 320 m.
(a) \[6300{{m}^{2}}\] (b) \[6500{{m}^{2}}\]
(c) \[6400{{m}^{2}}\] (d) \[6200{{m}^{2}}\]
(e) None of these
Answer (c)
Explanation: Let the length of each side of the square park be a metre. Then, perimeter = 320 m
\[\Rightarrow 4a=320\]
\[\Rightarrow a=\frac{320}{4}=80m\] [\[\therefore \] Perimeter of a square\[=4\times Side\]]
\[\therefore Area={{a}^{2}}=\left( 80\times 80 \right){{m}^{2}}=6400{{m}^{2}}.\]
Find the breadth of a rectangular plot of land, if its area is 440 sq. m and length is 22 m. Also, find its perimeter.
(a) 20 m, 84 m (b) 2 m, 46 m
(c) 50 m, 42 m. (d) 4 m, 40 m
(e) None of these
Answer (a)
Explanation: We have,
I = Length of the plot = 22 m. Area of the plot = 440 sq. metre
Let the breadth of the plot be b metres. Then,
\[Breath=\frac{Area}{Length}\Rightarrow b=\frac{420}{22}=20m\]
Perimeter \[=2\left( I+b \right)=2\left( 22+20 \right)m=2\times 42m=84m.\]
Hence, the breadth of the plot is 20 m and the perimeter is 84 m.
The carpet for a room 6.6 m by 5.6 m costs Rs. 3960 and it was made from a roll 70 cm wide. Find the cost of the carpet per metre.
(a) Rs. 70 (b) Rs. 78
(c) Rs. 75 (d) Rs. 70
(e) None of these
Answer (c)
Explanation: We have,
Area of the carpet \[=6.6\times 5.6=36.96{{m}^{2}},\] Width of the roll = 70 cm = 0.7 m
\[\therefore \]Length of the roll \[=\frac{Area}{With}=\frac{36.96}{0.7}m=52.8m\]
Cost of the carpet \[=Rs.\,3960\]
\[\therefore \]Cost of the carpet per metre \[=Rs.\,\frac{3960}{52.8}=Rs.\,75\]
Hence, the carpet costs \[Rs.\,75\] per metre.
A rectangular lawn of length 40 m and breadth 25 m is to be surrounded all around by a path which is 2 m wide. Find the area of the path.
(a) \[276\text{ }{{m}^{2}}\]
(b) \[345\text{ }{{m}^{2}}\]
(c) \[308\text{ }{{m}^{2}}\]
(d) All of these
(e) None of these
Answer (a)
Explanation: Area of the path \[=2\left( 44\times 2 \right)+2\left( 25\times 2 \right)=176+100=276{{m}^{2}}.\]
A garden is 60 m by 30 m. It has two paths at the centre as shown in the figure. If the width of the path is 2 m, how much area is left for gardening?
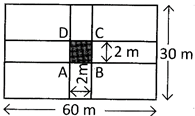
(a) \[1441\text{ }{{m}^{2}}\]
(b) \[1624\,{{m}^{2}}\]
(c) \[1328\,{{m}^{2}}\]
(d) All of these
(e) None of these
Answer (b)
Explanation: Area for gardening \[=4\left( 14\times 29 \right)=1624{{m}^{2}}.\]
You need to login to perform this action.
You will be redirected in
3 sec
