Geometry
Category : 6th Class
Geometry
Learning Objectives
Geometry
The branch of mathematics which deals with mathematical objects like points, lines, panes and space is called geometry.
Point: A point is to be thought of as a location in space. In other words, a point determines location in a space.
Line segment: Let A and B be two point on a plane. Then the straight path between points a and B is known as Sine segment AB.
![]()
The above line segment is denoted as\[\overline{AB}\].
Ray: A line segment extended endlessly in one direction Is. called a ray.
![]()
The above ray Is denoted as \[\overrightarrow{AB}\].
Line: A line is a straight path that extends on and on in both directions endlessly.
![]()
The above ray Is denoted as \[\overrightarrow{AB}\].
Line: A line is a straight path that extends on and on in both directions endlessly.
|
Parallel lines: If two or more lines do not meet each other however far they are extended, then they are called parallel lines |
|
|
Intersecting lines: If two or more lines meet each other at one point they are called intersecting lines. |
|
|
Concurrent lines: Three or more lines in a place are concurrent if all of them pass through the same point. The common point is called point of concurrence. |
|
|
Collinear points: Three or more points which lie on the same line are collinear, and the line is called the line of collinearity for the given points. |
|
|
Angle: The figure formed by two rays with the same initial point is called an angle. |
|
|
Types of angles |
|
|
Acute angle: An angle which measures more than \[=30{}^\circ \times 3=90{}^\circ .\]but less than \[90{}^\circ \]is called an acute angle. |
|
|
Right angle: An angle which measure \[90{}^\circ \] is called a right angle. |
|
|
Obtuse angle: An angle which measures more than \[90{}^\circ \] but less than \[180{}^\circ \] is called an obtuse angle. |
|
|
Straight angle: An angle which measures \[180{}^\circ \] is called a straight angle. |
|
|
Reflex angle: An angle which measures more than \[180{}^\circ \] but less than \[360{}^\circ \] is called a reflex angle. |
|
|
Complete angle: An angle which measures \[360{}^\circ \] is called a complete angle. |
|
|
Zero angle: An angle which measures \[0{}^\circ \]is called zero angle. |
|
|
Triangle: A triangle is a closed plan figure bound by three lines segments. In fact triangle is a polygon. |
|
|
Types of trianlges |
|
|
Equilateral triangle: A triangle whose all sides are of equal length is known as equilateral triangle. |
|
|
Isosceles triangle: A triangle whose all sides are of equal length is known as isosceles triangle. |
|
|
Scalene triangle: A triangle whose all sides are of different length is known as scalene triangle. |
|
|
Acute angled triangle: If all the three angles of a triangle are acute then the triangle is known as acute angled triangle. |
|
|
Obtuse angled triangle: The triangle having an obtuse angle in known as obtuse angled triangle. |
|
|
Right angled triangle: The triangle having a right angle is known as right angled triangle. |
|
|
Quadrilateral: A quadrilateral is a closed plane figure bounded by four lines segments or a quadrilateral is a four sided polygon. |
|
|
Types of quadrilatreral |
|
|
Trapezium: A quadrilateral, in which one and only one pair of opposite sides are parallel, is known as trapezium. |
|
|
Parallelogram: A quadrilateral in which both pair of opposite sides are parallel is called a parallelogram. |
|
|
Rhombus: A parallelogram, whose all sides are of equal length, is known as rhombus. |
|
|
Rectangle: A parallelogram, in which each of the angles is a right angle, is known as rectangle. |
|
|
Square: A parallelogram, in which all sides are equal and each angle is a right angle, is known as square. |
|
|
Circle: A circle is simple closed curve all of whose points are at the same distance from a given point in the same plane. |
|
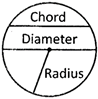
Parts of a circle
Centre: The fixed point in the plane which is equidistant from every point lying on the boundary of the circle is called centre of the circle.
Radius: The line segment joining the centre of the circle to any point on the circle is the radius of that circle.
Chord: A line segment joining any two points on a circle is called chord of the circle.
Diameter: A chord which passes through the centre of a circle is called a diameter of that circle.
Secant: A line which intersects the circles at two distinct points is called a secant.
Arc: An arc is a part of a circle.
Segment: A region in the interior of the circle enclosed by a chord and an arc is called a segment of the circle.
Sector: A region in the interior of the circle enclosed by two radii and an arc is called sector of the circle.
Semicircle: A diameter divides a circle into two equal parts. Each part is called a semicircle.
Circumference: The length of the boundary of the interior of a circle is called circumference of the circle.
Concentric circles: Two or more circles with the same centre are called concentric circles.

Three Dimensional Shapes
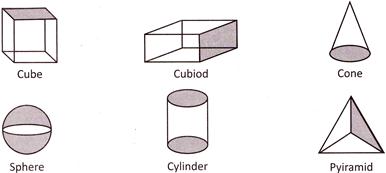
Cuboid: Cuboid is a three dimensional solid shape. A rectangular wooden box is an example of a cuboid. A cuboid has 6 rectangular faces, 12 edges and 8 vertices.
Cube: A cuboid whose length, breadth and height are equal is called a cube, A cube has 5 square faces, 12 edges and 8 vertices.
Cylinder: A cylinder is three dimensional geometric figure that has two congruent and parallel bases. It has no vertex, two circular faces, one curved face and two curved edges.
Sphere: An object which is in the shape of a ball is said to have the shape of sphere. It has a curved surface but no vertex and no edge.
Cone: A cone is a three dimensional geometric shape that tapers smoothly from a fiat to a point called the apex or vertex. It has one vertex, one curved edge, one curved face and one flat face.
Pyramid: A pyramid is a solid whose base is a plane rectilinear figure and whose side faces are triangles having a common vertex called the vertex of the pyramid.
Symmetry
A figure drawn on the paper is symmetric, if it can be folded in such a way that the two halves of the figure exactly cover each other. The line of fold is called axis of the symmetry,

Symmetry of some geometrical shapes
Line segment: A line segment is symmetrical about its perpendicular bisector.
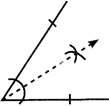
Angle: An angle with equal arms is symmetrical about the bisector of the angle,
Scalene triangle: A scalene triangle has no line of symmetry.
Parallelogram: A parallelogram has no line of symmetry.
Table of Symmetry of Geometrical Shapes
|
Shape |
Figure |
Number of lines of symmetry |
|
Equilateral triangle |
|
3 |
|
Isosceles triangle |
|
1 |
|
Square |
|
4 |
|
Rectangle |
|
2 |
|
Rhombus |
|
2 |
|
Semicircle |
|
1 |
|
Circle |
|
Infinite |
Commonly Asked Questions
Which one of the following is the complementary angle of \[\mathbf{30}{}^\circ \] ?
(a) \[30{}^\circ \] (b) \[60{}^\circ \]
(c) \[90{}^\circ \] (d) All of these
(e) None of these
Answer (b)
Explanation: Complementary angle of \[30{}^\circ =90{}^\circ -30{}^\circ =60{}^\circ .\]
In the options given below the pair of angles are given. Find the complementary pair.
(a)\[51{}^\circ ,25{}^\circ \]
(b) \[61{}^\circ ,29{}^\circ \]
(c) \[45{}^\circ ,55{}^\circ \]
(d) All of these
(d) None of these
Answer: (b)
Explanation: If the sum of pair of angles is \[90{}^\circ \] then the pair is called cornplementary pair of angles. The sum of angles \[61{}^\circ +29{}^\circ =90{}^\circ .\] Hence the pair of angles \[61{}^\circ ,29{}^\circ \] is a complementary pair of angles,
Choose the pair of supplementary angle from the options given below?
(a) \[100{}^\circ ,200{}^\circ \]
(b) \[105{}^\circ ,75{}^\circ \]
(c) \[30{}^\circ ,180{}^\circ \]
(d) All of these
(e) None of these
Answer: (b)
Explanation: The sum of angles of the pair \[105{}^\circ ,75{}^\circ =105{}^\circ +75{}^\circ =180{}^\circ \] Hence, the pair of angles \[105{}^\circ ,75{}^\circ \] is a supplementary pair of angles.
Find the measurement of A if B and C are given when A, B and C are the angle of the triangle.
(a)\[A=180{}^\circ -\left( B+C \right)\] (b) \[A=180{}^\circ +\left( B-C \right)\]
(c) \[A=180{}^\circ +C-B\]
(d) All of these
(e) None of these
Answer (a)
Explanation: The sum of angles of the triangle \[=180{}^\circ \]. Hence, the angle \[A=180{}^\circ -\left( B+C \right).\]
If the base of a triangle is 18 cm and distance between base and opposite vertex is 10 cm, what will be the area of triangle?
(a) \[206\text{ }c{{m}^{2}}\]
(b) \[10\text{ }c{{m}^{2}}\]
(c) \[90\text{ }c{{m}^{2}}\]
(d) All of these
None of these
Answer (c)
Explanation: The distance between base and opposite vertex is height,
\[The\,area={{\frac{1}{2}}^{~}}\times base\times height\]
\[=\frac{1}{2}18\times 10=90c{{m}^{2}}.\]
You need to login to perform this action.
You will be redirected in
3 sec
