7th Class Mathematics Decimals and Fractions STATISTICS

Learning objective

• To learn to terms data, frequency, frequency distribution, mode class interval, etc.
• To learn how to arrange observations (data) in grouped data.
• To learn how to find Arithmetic mean of the given data.
• To understand the way to represent the given data in the form of pictograph and Bar graph.
• To learn how to interpret the data given in the graph (pictograph and Bar graph).

INTRODUCTION

Extraction of meaningful information by collection of data, organising, summarizing, presenting and analyzing the data is a branch of mathematics called statistics. Data is defined as the particular information in numeric form.

PRIMARY DATA

If the data is collected by the investigator herself/himself with the specific purpose, then such data is called the primary data.

SECONDARY DATA

If the data collected by someone else other than investigator are known as secondary data.

GROUPED DATA

The data can be represented into classes or groups. Such a presentation is known as grouped data. Firstly it may arrange in ascending or descending order and then divide into groups.

RAW DATA

Raw data is the data which is not arranged in any particular fashion or pattern. It is the original form of data.

FREQUENCY

It is a number which tells that how many times does a particular observation appear in a given data.

For example:

In a data 5, 1, 4, 5, 1, 3, 2, 2, 5, 1, 1, 6, 4, 3, 4, 7, 6 the frequency of 1 in this data is 4 because it occurs four times in the observation.

The observation having maximum frequency is known as mode. For example: 7, 6, 5, 5, 4, 3, 2, 2, 5, 1, 3.

5 occurs three times in the given data.

\[\therefore \]  5 is the mode.

FREQUENCY DISTRIBUTION

A tabular arrangement of data sharing their corresponding frequencies is called a frequency distribution.

CLASS INTERVAL

The group in which the raw data is condensed is called a Class interval. Each class is bounded by two figures.

GROUPING OF DATA

Let us observe the marks obtained by 25 students in Mathematics as follows:

56, 31, 41, 64, 53, 56, 64, 31, 88, 53, 28, 33, 70, 70, 61, 74, 74, 64, 56, 32, 53, 53, 56, 61, 53.

We observe that there are few students who get same marks, e.g., 74 marks is obtained by 2 students, 53 is obtained by 5 students etc. Let us represent them in a frequency distribution table given below:

Here, we see that the lowest marks is 28 and the highest marks is 88.

We can further group them into classes as given below:

AVERAGE OR ARITHMETIC MEAN IS DEFINED AS FOLLOWS

\[\text{Mean}=\frac{\text{sum}\,\text{all}\,\text{observations}}{\text{number}\,\text{of}\,\text{observations}}\]

For example: Find the mean of the data: 13, 16, 12, 14, 19, 12, 11, 10 13 + 16 + 12 + 14 + 19 + 12 + 11 + 15

Sol.        Mean \[=\frac{13+16+12+14+19+12+11+15}{8}\]

\[=\frac{112}{8}\]

 Mean = 14

PICTOGRAPH

A pictograph is the way of representing data using pictures.

READING AND INTREPRETING PICTOGRAPH

Reading a pictograph helps in intrepreting the pictograph so as to get information from it.

(i) Find the number of people preferring Red colour.

(ii) How many liked Grey colour?

(iii) What is the ratio of the number of people preferring White colour to the number of people preferring Silver colour?

Sol.        We observe from the pictograph that:

(i)  The number of people preferring red colour \[=7\times 10=70\]

(ii) Number of people preferring grey colour \[=5\frac{1}{2}\,\times 10=55\]

(iii) Number of people preferring white colour \[=2\times 10=20\]

\[\therefore \] Ratio of the number of people preferring white colour to the number preferring Silver colour

= 20 : 55 = 4 : 11

BAR GRAPH

When numerical data is presented as columns on a graph, this graphical representation of data is called a bar graph.

PROPERTIES OF BAR GRAPHS

In a bar graph, the columns are drawn such that:

1. each column is of equal width.
2. there is equal space between each column.
3. the height of each column indicates the value of data such that if a perpendicular is drawn from its top, the percentage of marks represented by the column can be read off.
4. all bars or columns are drawn on the same common base.

CONSTRUCTION OF A BAR GRAPH

Steps:

1. On the graph paper draw a horizontal line (x-axis) and a vertical line (y-axis)
2. Along the horizontal line, mark points at equal distances and write the names of the items for which the data is to be represented.
3. Choose a suitable scale which shall determine the height of the bars.
4. Locate the heights of different bars according to scale.
5. On x-axis draw bars of equal width according to the required height.
6. Keep the distance between the bars the same.

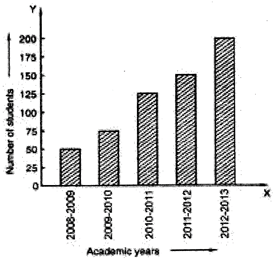
Example: The following table gives the umber of students in Class VI in a school during academic years 2008 to 2013.

Represent the above data by a bar graph.

Sol.       

To represent the above data by a bar graph, we first draw a horizontal and a vertical line. Since five values of the numerical data are given. So, we mark five points on the horizontal line at equal distances and erect rectangles of the same width at these points. The heights of the rectangles are proportional to the numerical values of the data as shown in Fig.

READING OF BAR GRAPHS

Reading of the bar graph is the process of interpreting the bar graph together information

Example: Read the following bar graph shown in Fig. and answer the following questions:

(i) What is the information given by the bar graph?

(ii) In which month was the sale of the book maximum?

(iii) In which month was the sale of the book minimum?

Sol.

(i)  The bar graph shows the number of copies of Physics for Class XII sold by a bookseller during the period from April 2014 to August 2014.

(ii) The sale of the book was maximum in the month of April as the height of the rectangle corresponding to April month is maximum.

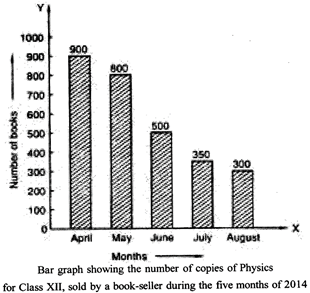
(iii) The sale of the book was minimum in the month of August as the height of the corresponding rectangle is minimum.