Playing with Numbers
Category : 6th Class
Playing with Numbers
e.g.. We know that 35 = 1\[\times \]35 and 35 = 5 \[\times \] 7.
This shows that each of the numbers 1, 5, 7 and 35 divides 35 exactly.
Therefore 1, 5, 7 and 35 are all factors of 35 and 35 is a multiple of each one of the numbers
1, 5, 7 and 35.
e.g., 2, 4, 6,8,10, etc.
e.g., 1,3,5,7,9,11, etc.
prime number.
e.g., 2,3,5,7,11,13,17,19,23,29 etc.
e.g., 4, 6, 8,9,10 etc.
Note: (i) 1 is neither prime composite. (since 1=1, the two factors are not distinct.)
(ii) 2 is the lowest prime numbers.
(iii) 2 is the only even prime number. (All other even number are composite numbers.)
e.g., (i) 3, 5 (ii) 5, 7 (iii) 11, 13 etc.
A set of three consecutive prime numbers, differing by 2, is called a prime triplet.
An example of prime triplet is (3, 5, 7).
e.g., 6 is a perfect number, since the factors of 6 are 1,2,3,6 and (1 + 2 + 3 + 6) = (2 x 6).
e.g., (i) 2, 3 (ii) 3, 4 (iii) 8, 15
Note: (i) Two prime numbers are always co – prime.
(ii) Two co – prime need not be prime numbers.
e.g., 6, 7 are co-primes, while 6 is not a prime number
e.g., (i) 6 = 3 + 3 (ii) 8 = 3+5
Tests of divisibility of numbers
e.g., 42,84,120,1456,568 etc. are divisible by 2.
A number is divisible by 3, if the sum of its digits is divisible by 3.
e.g., Consider the number 64752.
Sum of its digits = (6 + 4 + 7 + 5 + 2) = 24, which is divisible by 3.
\[\therefore \]64752 is divisible by 3.
A number is divisible by 4, if the number formed by its digits in tens and units places is divisible by 4.
e.g., Consider the number 49812.
The number formed by tens and units digit is 12, which is divisible by 4.
\[\therefore \]49812 is divisible by 4.
A number is divisible by 5, if its unit’s digit is 0 or 5.
e.g., 15, 35, 80,90,1435 etc., are divisible by 5.
Test of divisibility by 6:
e.g., Consider the number 26574.
Its units digit is 4. So it is divisible by 2.
Sum of its digits =2+6+5+7+4= 24, which is divisible by 3.
Therefore, 26574 is divisible by both 2 and 3.
And hence it is divisible by 6.
A number is divisible by 8, if the number formed by its digits in hundreds, tens and unit's places is divisible by 8.
e.g., Consider the number 47192.
So, 47192 is divisible by 8.
A number is divisible by 9, if the sum of its digits is divisible by 9.
e.g.. Consider the number 72306.
Sum of its digits =7+2+3+0+6 = 18, which is divisible by 9. Therefore, 72306 is divisible by 9.
A number is divisible by 10, if its units digit is zero.
e.g., 10,20,130,580,700,7050, etc., are divisible by 10.
A number is divisible by 11, if the difference of the sum of its digits in odd places and sum of its digits in even places (starting from units place) is either 0 or a multiple of 11.
e.g., Consider the number 530728.
Sum of the digits in odd places = 8 + 7 + 3 = 18
Sum of the digits in even places = 2 + 0 + 5 = 7
Difference of these sums = 18 – 7 = 11 which is divisible by 11.
Therefore, 530728 is divisible by 11.
The Least Common Multiple (L.C.M.) of given numbers can be found by the following methods.
(i) By Listing Multiples: List the multiples of the given numbers and then find the least
of the common multiples.
(ii) Multiples of 36 are 36, 72, 108, 144,180, 216,
Multiples of 72 are 72, 144, 216, 288, 360, 432,
Observe that the common multiples are highlighted.
\[\therefore \]The least of the common multiples is 72. Hence L.C.M. of 36 and 72 is 72.
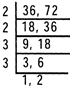
\[\therefore \]L.C.M. =2x2x3x3x2= 72
L.C.M. of 36 and 72 =72
The highest common factor of the given numbers can be found by the following methods.
(i) By Listing Factors: List out the factors of the given numbers and find the highest of the common factors.
Factors of 24 are 1, 2,3,4,6, 8, 12 and 24.
Factors of 36 are 1,2,3,4,6,9,12,18 and 36. Observe that the common factors are highlighted. Common factors of 24 and 36 = 1, 2,3,4,6 and 12.
The highest of the common factors is 12.
\[\therefore \]The highest common factor of 24 and 36 is 12,
(ii) Division Method: Divide the larger of the given numbers by the smaller one. Subtract and then divide the smaller number by the remainder. Continue until the remainder is 0.The last divisor is the required H.C.F. of the given numbers.
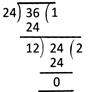
\[\therefore \]H.C.F. of 24 and 36 =12
(iii) By Prime Factorisation Method (Division Method):
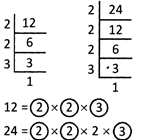
The product of the common factors =2x 2 x 3=12.
\[\therefore \]H.C.F. of 12 and 24 is 12.
Note: (i) The H.C.F. of given numbers is not greater than any of the given numbers.
(ii) The H.C.F. of two co – primes is 1.
(iii) The L.C.M. of given numbers is not less than any of the given numbers.
(iv) The L.C.M. of two co – prime is equal to their product.
(v) The H.C.F. of two given numbers is always a factor of their L.C.M.
e.g., Consider the numbers 24 and 36.
L.C.M. of 24 and 36 =72
H.C.F. of 24 and 36 =12
Product of numbers = 24 \[\times \] 36 = 864
Product of H.C.F. and L.C.M. = 12 \[\times \] 72 = 864
\[\therefore \]Product of two numbers = Product of their H.C.F. and L.C.M.
You need to login to perform this action.
You will be redirected in
3 sec
