MENSURATION
Category : 6th Class
Learning Objective
AREA AND PERIMETER OF PLANE FIGURE
PERIMETER
The perimeter of a plane geometrical figure is the total length of sides (or boundary) enclosing the figure. Units of measuring perimeter can be mm, cm, m, km etc.
AREA
The area of any figure is the amount of surface enclosed within its bounding lines. Area is always expressed in square units.
1. TRIANGLE
Perimeter of a triangle is equal to the sum of its sides.
For a triangle having sides a, b and c,
Perimeter \[=a+b+c\]
and area \[(A)\,=\sqrt{s(s-a)(s-b)\,(s-c)}\]
where \[s=\frac{a+b+c}{2}\]
area of equilateral triangle with each side a is \[\frac{\sqrt{3}}{4}{{\text{(side)}}^{2}}\].
Observe the given figure
Area of \[\Delta ABC\]\[=\frac{1}{2}\times base\times height\]
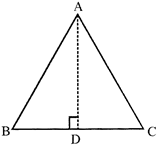
\[=\frac{1}{2}\times BC\times AD\]
Observe the given figure,
\[\Delta \,ABC\] is a right angled triangle, right angled at B.
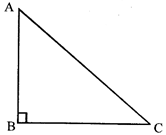
Area of \[\Delta \,ABC=\frac{1}{2}\,BC\times AB\]
For Example:
Find the perimeter and area of triangle ABC.
Sol: \[P=AB+BC+CA\] = 7 + 4 + 5 = 16 cm Base = BC, Height =AD
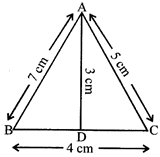
Area
\[=\frac{1}{2}\times BC\times AD\]
\[=\frac{1}{2}\times 4\times 3\]
\[=6c{{m}^{2}}\]
2. RECTANGLE
Area of rectangle \[ABCD=AB\times BC=l\times b\]
Perimeter of rectangle = sum of all sides
\[=l+b+l+b\] \[=2l+2b\] \[=2(l+b)\]
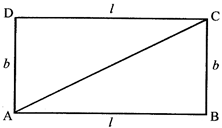
Diagonal (AC) of rectangle \[=\sqrt{{{l}^{2}}+{{b}^{2}}}\]
For example:
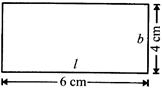
For the adjoining rectangle find:
(i) the perimeter;
(ii) the area.
Sol. Perimeter \[=2(l+b)\,=2(6+4)\,=2\times 10=20\,cm\] Area \[=l\times b=6\times 4=24\,c{{m}^{2}}\]
3. SQUARE
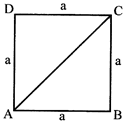
Perimeter of square ABCD with side \[a=4a\]
Area of square with side \[a={{a}^{2}}\]
Diagonal of square
\[=AC=\sqrt{{{a}^{2}}+{{a}^{2}}}=\,\sqrt{2{{a}^{2}}}\,=a\sqrt{2}\]
\[=\sqrt{2}\times \] side of square
For example
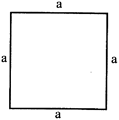
For the adjoining square find:
(i) the perimeter;
(ii) the area
Sol. Perimeter \[=4a=4\times 5=20\,cm\]
Area \[={{a}^{2}}=5\times 5=25\,c{{m}^{2}}\]
AREA AND CIRCUMFERENCE OF CIRCLE
CIRCLE
A circle is a path in a plane travelled by a point which moves in such a way that its distance from a fixed point is always constant.
The fixed point is called centre of circle and fixed distance is called radius of the circle,
Circumference or perimeter of circle of radius ‘r’, is
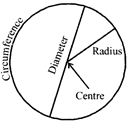
\[C=2\pi r=\pi d\](\[(2r=d,d=\]diameter)
Area of circle of radius \['r'=\pi {{r}^{2}}\]
SEMI-CIRCLE
A semicircle is a figure enclosed by a diameter and part of circumference of the circle cut-off by it.
Area of semicircle of radius \['r'=\frac{\pi {{r}^{2}}}{2}\]
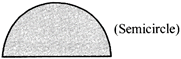
Circumference of semicircle of radius \['r'=\pi r\]
SURFACE AREA AND VOLUME OF SOLIDS
CUBOID
A cuboid is a three dimensional box. It has six rectangular faces. It is defined by the virtue of its length \[(\ell )\], breadth (b) and height (h). It can be visualized as a room. It is also called rectangular parallelepiped.
Total surface area \[(TSA)\,=2\,(lh=lb+bh)\] Sq. units.
Lateral surface area (LSA) is the area of four walls (excluding area of base and top)
= 2h (1+b) Sq. units.
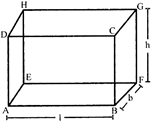
Length of diagonal of cuboid \[=\sqrt{{{1}^{2}}+{{h}^{2}}+{{b}^{2}}}\]
Volume of cuboid = Space occupied by cuboid = Area of base x height \[=(1\times b)\,\times h=1\times b\times h\] cubic units
For example
Find the surface area of a room having dimension \[12m\times 8m\times 5m\].
Sol.
Total surface area of room \[=2(lb+bh+lh)\]
\[=2(12\times 8+8\times 5+12\times 5)\]
=2(96 + 40 + 60)
\[=2\times 196\]
\[=392{{m}^{2}}\]
CUBE
A cube is a cuboid which has all its edges equal i.e. length = breadth = height = 'a' say.
Area of each face of the cube is \[{{a}^{2}}\] square units.
Total surface area (TSA) of square = Area of 6 square faces of cube TSA \[=6\times {{a}^{2}}=6{{a}^{2}}\,sq\].units.
Lateral surface area of cube (LSA) = Area of four faces (excluding bottom and top face)
\[LSA=4\times {{a}^{2}}\]
\[LSA=4{{a}^{2}}\] sq. units.
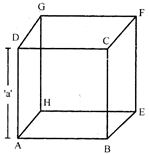
Length of diagonal (d) of cube
\[=\sqrt{{{a}^{2}}+{{a}^{2}}+{{a}^{2}}}\,=\sqrt{3{{a}^{2}}}\]
\[=a\sqrt{3}\]
Volume of cube (V) = Base Area x Height
\[V={{a}^{2}}\times a={{a}^{3}}\] cubic units
For example
For the adjoining cube find:
(i) Total surface area
(ii) Lateral surface area
(iii) Volume
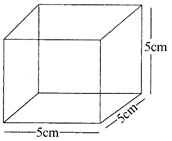
Sol.
(i) Surface area
\[=6\times {{(side)}^{2}}=6\times {{(5\,cm)}^{2}}\,=150c{{m}^{2}}\]
(ii) Lateral surface area
\[=4\times \,{{(side)}^{2}}=4\times {{(5cm)}^{2}}=100c{{m}^{2}}\]
(iii) Valume \[={{(side)}^{2}}={{(5\,cm)}^{3}}=125c{{m}^{3}}\].
You need to login to perform this action.
You will be redirected in
3 sec
