Mensuration
Category : 6th Class
Mensuration
Perimeter and Area of Plane Figures
Perimeter of geometrical figure is the sum of its sides. There are different types of geometrical figures. Figures are classified by their shapes and sizes. Area of a geometrical figure is its total surface area.
Perimeter and Area of a Triangle
Perimeter and Area of a Parallelogram
Parallelogram is a quadrilateral whose opposite sides are equal and parallel to each other.
In the given figure ABCD is a Parallelogram in which \[\text{AB}\parallel \text{CD,}\,\,\text{BC}\parallel \text{AD,}\,\,\text{AB}=\text{CD}\] and \[\text{AD=BC}\]
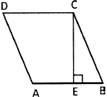
Perimeter of a Parallelogram = 2 (sum of two adjacent sides)
Hence, perimeter of a parallelogram \[\text{ABCD=2(AB+BC)}\]Area of a parallelogram = Base \[\text{ }\!\!\times\!\!\text{ }\] Height
Therefore, the area of a parallelogram \[\text{ABCD=AB }\!\!\times\!\!\text{ CE}\]
Perimeter and Area of a Rectangle
A rectangle has four right angles and its opposite sides are equal.
Longer side of a rectangle is called length and shorter side is called width.

Perimeter of rectangle
\[ABCD=AB+BC+CD+DA\]
= length + width + length + width = 2(length + width)
Hence, perimeter of a rectangle = 2(length + width)
Area of a rectangle = length \[\times \]width
Perimeter and Area of a Rhombus
A rhombus is a parallelogram with four equal sides.
Therefore, perimeter of rhombus\[=4\times side\]. In the figure given below ABCD is a rhombus.
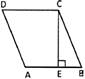
Perimeter of a rhombus, \[=4\times side\]
Area of a rhombus = base \[\times \] height
Also area of a rhombus \[\text{=}\frac{1}{2}\times \] product of length of diagonals.
Perimeter and Area of a Square
A square has four equal sides and each angle of\[90{}^\circ \].
In the picture given below, ABCD is a square because its all sides are equal and each angle is a right angle.
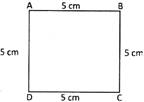
Perimeter of square = side + side + side + side\[=4\times side\]
Area of a Square = side \[\times \]side = \[{{(side)}^{2}}\]
Perimeter and Area of a Trapezium
A quadrilateral whose one pair of sides are parallel is called a trapezium. The given figure is a trapezium in which parallel sides are AB and CD and non-parallel sides are AD and BC
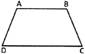
Perimeter of a trapezium = Sum of the length of all sides
Area of a trapezium \[=\frac{1}{2}\times \] (Sum of lengths of parallel sides) \[\times \]distance between parallel sides.
Cirumference and Area of a circle
A round plane figure whose all points are equidistant from a fixe point is called a circle and the fixed point is called centre of the circle and fixed distance is called radius of the circle.
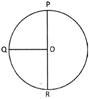
Diameter = 2 \[\times \]Radius.
Circumference or perimeter of a circle\[=2\pi r=\pi d\].
Area of circle\[=\pi {{r}^{2}}\]
Area of a semicircle \[=\frac{\pi {{r}^{2}}}{2}\]
Perimeter of a semicircle \[=\frac{2\pi r}{2}+\]\[2r=\pi r+2r\]\[=r(\pi +2)\]
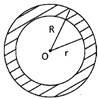
Area of a circular ring = Area of outer circle \[-\] Area of inner circle
\[\pi {{R}^{2}}-\pi {{r}^{2}}=\pi ({{R}^{2}}-{{r}^{2}})=\pi (R+r)(R-r)\]
Example: What will be the height of a triangle if the area of triangle is 18 \[c{{m}^{2}}\]and base is 12 cm?
(a) 3 cm (b) 9 cm
(c) 10 cm (d) 4 cm
(e) None of these
Answer (a)
Explanation: Area of a triangle = \[\frac{1}{2}\]\[\times \]base \[\times \] height
\[\Rightarrow 18=\frac{1}{2}\times 12\times \] height \[\Rightarrow \]height = 3 cm.
You need to login to perform this action.
You will be redirected in
3 sec
