6th Class Mathematics Integers

Integers

• The set of positive numbers, 0 and negative numbers is called the set of integers.

The set of integers is denoted by I or Z.

Z ={.....,-3,-2,-1, 0,1,2,3,......}

• Natural numbers are contained in the whole numbers. Therefore, N (= W.)

• Whole numbers are contained in the integers.

Therefore, We Z.

• Negative numbers are placed at the bottom of 0 on the vertical number line. Zero is neither positive nor negative.

• To represent quantities like profit, income, increase, rise, high, north, east, above, depositing climbing and so on, positive numbers are used.

• To represent quantities like loss, expenditure, decrease, fall, low, south, west below withdrawing, sliding and so on, negative numbers are used.

• Facts about Integers:

(a) Every positive integer is larger than every negative integer and zero.

(b) Zero is less than every positive integer.

(c) Zero is larger than every negative integer.

(d) Zero is neither negative nor positive.

(e) Farther a number from zero on the right, larger is its value.

(f) Farther a number from zero on the left, smaller is its value.

(g) When no sign is given before a number, it is considered as a positive number.

(h) It is compulsory to write a '-' (minus) sign before a negative number.

(h) Usually, negative numbers are placed within simple brackets to avoid confusion arising due to the operator before it.

• Ordering integers:

(a) Comparing numbers of different signs: A positive number is always greater than a negative number and zero.

e.g., 6 > - 12; 6 > 0 etc.

(b) Comparing two positive integers: The positive number with larger value is larger and that with the smaller value is smaller.

e.g., 73 > 57; 45 > 36 etc.,

• Comparing two negative integers: The negative number with larger value is smaller and that with smaller value is larger.

e.g.,-6 < - 2; - 12 > -18 etc.,

Note: If a a > b then – a < - b.

eg., 8 > 5 => -8 <-5

• Addition on the number line:

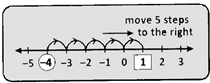
(a) Adding a positive number to a given number is represented by moving to the right on the number line.

e.g., - 4 + 5 = 1

• (b) Adding a negative number to a given number is represented by moving to the left on the number line.

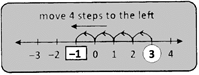
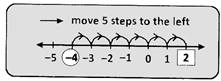
e.g., 3+(- 4) = 3 – 4 = - 1

• Operations on integers:

(a) Addition: We know that, negative numbers are placed within simple brackets to avoid confusion arising due to the operator before it.

(i) Two positive numbers are added and a positive sign is given to the sum.

e.g., (+5) + (+2) = +7

(ii)   Two negative numbers are added and a negative sign is given to the sum. e.g., (-12) + (-3) =-15

(iii) One positive and one negative number are subtracted, and the sign of the larger number is given to the difference.

e.g., (+24) + (-3) = +21; (-32) + (+8) = -24

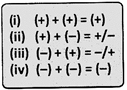
 (b) Subtraction:

(i) Two positive numbers are subtracted and the sign of the larger number is given to the difference.

e.g., (+ 3) - (+ 4) = 3 – 4 =- 1

(ii) Two negative numbers are subtracted and the sign of the larger number is given to the difference.

e.g., ( - 5) - (- 7) = - 5 + 7 = 2

(iii) One positive and one negative number are subtracted by adding them and the sign of the larger number is given to the sum.

e.g., (+12) - (- 6) =+12 + 6 = 18

(-12) - (+6) = - 12 - 6 = - 18

Note: Subtracting a number means adding its additive inverse.

(c) Subtraction on the number line:

(i) Subtracting a positive number from a number is represented by moving to the left on the number line.

e.g., -2 - (+5) = -2 - 5 = -7

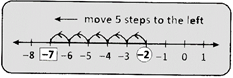
(ii) Subtracting a negative number from a number is represented by moving to the right on the number line.

e.g., - 4 - (- 6) =- 4 + 6 = 2

• The smallest positive integer is 1. The biggest negative integer is -1.

• The greatest positive integer does not exist. The smallest negative integer does not exist.

• Simplification of numerical expressions:

Using BODMAS rule we simplify the numerical expressions.

• The order of removing the brackets of an expression is as follows:

() Parenthesis

{} Flower or curly brackets and

[ ] Square brackets

First we remove () then {} and lastly [ ].

• If a bracket is preceded by a negative term, then on removing the bracket the signs of the terms inside it will be changed.