GEOMETRY
GEOMETRY
Geometry is derived from two greek words "Geo" means "Earth" metron means "Measurement". That means measurement of Earth is called geometry.
Basics terms of geometry
- There are three basics undefined terms of geometry.
(i) Point (ii) Line (iii) Plane
Point: Point is a mark of position, it is made by sharp tip of pen, pencil and nail.
- It is denoted by capital letter.
- It is represented by
- A point has no length, no breadth and no thickness.
- Line segment: The distance between two points in a same plane is called a line segment.

- It is denoted by\[\overline{AB}\]. It is measured in 'cm' or 'inch'.
- It can be measured.
- 1 inch\[=2.5\,\,cm,\]
- Rays: A line segment extended endlessly in one direction is called a ray.

- It is denoted by\[\overline{OA}\].
- It can't be measured.
- Line: A line segment extended endlessly in both directions is called a line.

- It is denoted by\[\overline{AB}\]
- It can't be measured.
- Plane: A smooth flat surface which extended endlessly in all the directions is called a "plane".
Example:
(i) Surface of a blackboard in your class room.
(ii) Floor of the classroom.
Note: A plane has length and breadth.
A plane has no thickens or boundary.
- Collmearity of points: Three points A, B, C in a plane are collinear if they lie on the same straight line.
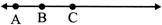
- Non-ColIinear points: The points which do not lie on the same line are called non - collinear point.

Note: Number of lines that can be drawn through 'n? non - collinear points is\[\frac{n\left( n-1 \right)}{2}\].
Properties of lines
Passing through a point an infinite number of lines can be drawn.
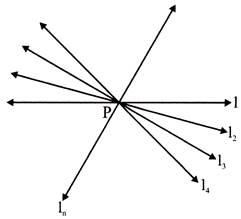
\[{{l}_{1}},\,\,{{l}_{2}}\]................... \[{{l}_{n}}\] all pass through 'p'.
- These lines are called concurrent line and the point P is called the point of concurrence.
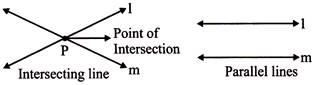
- Two lines in a plane are either intersecting or parallel.
ANGLE
- An angle is union of two different rays having the same initial point.
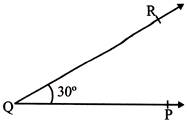
- Initial point is Q.
- Angle is denoted by\[\angle PQR=30{}^\circ .\]
- Unit of measurement of angle is degrees, which is represented as \[{}^\circ \] (e.g., \[60{}^\circ ,\] \[70{}^\circ ,\] \[80{}^\circ ,\]etc.)
Types of Angle
- Zero Angle: Initially the terminal ray coincides with initial ray without any rotation then the angle formed is a zero angle and its measure is\[0{}^\circ .\]
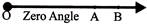
- Acute Angle: An angle is measure greater than \[0{}^\circ \] but less than \[90{}^\circ \] is called an Acute Angle.
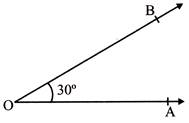
- Here, \[\angle AOB=30{}^\circ \]formed Acute Angle.
- Right Angle: An angle is measure \[90{}^\circ \] is called a right angle.
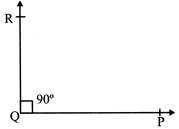
- Here, \[\angle PQR=90{}^\circ ,\]formed right angle.
- Obtuse Angle: An angle is measure greater than \[90{}^\circ \] but less than \[180{}^\circ \] is called an obtuse angle.
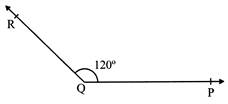
- Here, \[\angle PQR=120{}^\circ ,\]formed obtuse angle.
- Straight Angle: An angle is equal to \[180{}^\circ \]is called a straight angle.
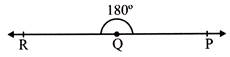
- Here, \[\angle PQR=180{}^\circ ,\]formed straight angle.
- Reflex Angle: An angle is measure more than \[180{}^\circ \] but less than \[360{}^\circ \] is called a reflex angle.
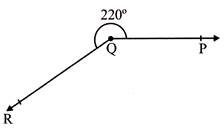
- Here, \[\angle PQR=220{}^\circ ,\] formed reflex angle.
- Complete angle: An angle is equal to \[360{}^\circ \]is called a complete angle.
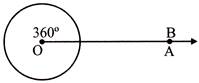
- Here, \[\angle AOB=360{}^\circ ,\]formed complete angle.
Some more part of Angle
- Vertically opposite angle: It two lines are interested at a point then vertically opposite angles are equal.
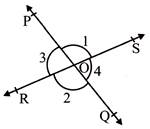
- \[\angle POS=\angle QOR\]and \[\angle POR=\angle QOS\]
- \[\angle 1=\angle 2\]and\[\angle 3=\angle 4\]
- \[\angle POS=\angle QOR\] and \[\angle POR=\angle QOS\] are formed vertically opposite angle.
- Adjacent angle: Two angles in a plane are said to be adjacent angles if they have a' common vertex.
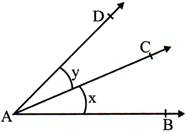
- In the adjoining figure x and y are called adjacent angles with common vertex A and common arm AC.
- Linear pair of angle: The pair of adjacent angles whose non common arms are two opposite rays is called a linear pair of angles.
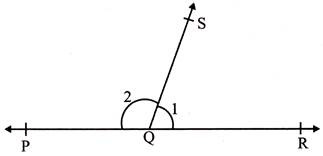
- In the adjoining figure \[\angle PQS\] and \[\angle RQS\] form a linear pair of angles.
- \[\angle 1+\angle 2=180{}^\circ \]
- Complementary angle: if the sum of measures of any two angles is \[90{}^\circ ,\]then they are said to be complementary angles.
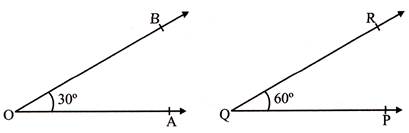
- \[\angle AOB+\angle PQR=30{}^\circ +60{}^\circ =90{}^\circ ~\]
- Supplementary Angle: If the sum of any two angles is \[180{}^\circ \]then they are said to be supplement angles.
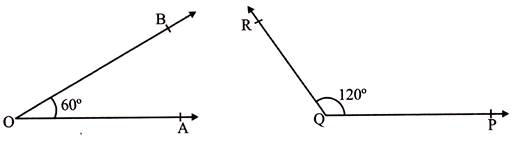
- \[\angle AOB+\angle PQR=60{}^\circ +120{}^\circ =180{}^\circ \]
Parallel lines:
Two lines which never meet, even when they are extended infinitely, are known as parallel lines.
- \[l//m\]
- The distance between two parallel line be same.
- The angle between two parallel line is\[0{}^\circ \].
Transversal;
A straight line which intersect two or more given lines at different points is called a transversal.
Example:
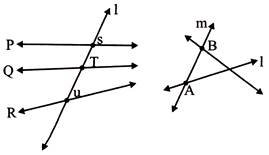
Classification of angles formed by a transversal
If two parallel lines cut by a transversal then some angles are formed.
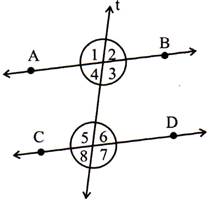
1. Corresponding Angles.
\[(\angle 2,\,\,\angle 6),\,\,(\angle 1,\,\,\angle 5),\,\,(\angle 3,\,\,\angle 7)\]and\[(\angle 4,\,\,\angle 8)\].
- Pair of corresponding angles are equal.
2. Alternate Interior Angles:
\[(\angle 3,\,\,\angle 5);(\angle 4,\,\,\angle 6)\]
- Pair of alternate angles are equal.
3. Alternate exterior angles:
\[(\angle 1,\,\,\angle 7);(\angle 2,\,\,\angle 8)\]
- Pair of alternate exterior angles are equal.
4. Co-interior angle or consecutive angle or allied angle.
\[(\angle 4,\,\,\angle 5)\]and\[(\angle 3,\,\,\angle 6)\]
- Pair of co-interior angles are need not be equal.
- Sum of co-interior angles is \[180{}^\circ .\]
\[\angle 4+\angle 5=180{}^\circ ,\]and\[\angle 3+\angle 6=180{}^\circ ,\]
Example: 1. In the given figure \[AB||CD,\] \[l\] is a transversal then\[x=\]?
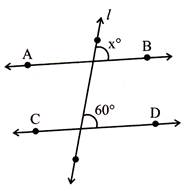
Solution: \[x=60{}^\circ \](by corresponding angle)
Example: 2. In the given figure \[AB||CD||EF\] then \[x+y\] is
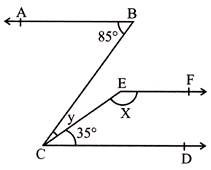
Solution: \[AB||CD\]and BC be the transversal then \[\angle ABC=\angle BCD\]
\[85{}^\circ =y{}^\circ +35{}^\circ \]
\[\therefore \]\[y=50{}^\circ \]
Now, \[EF||CD\]and CE be the transversal then
\[\angle DCE+\angle CEF=180{}^\circ \](by co-interior Angle)
\[35{}^\circ +x=180{}^\circ \]
\[x=145{}^\circ \]
\[\therefore x+y=50+145{}^\circ =195{}^\circ \]
Triangle
A closed figure bounded by three line segments is called a triangle.
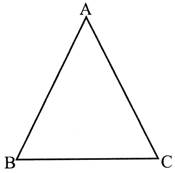
- We read as 'triangle ABC" and it is denoted by\[\Delta ABC.\]
- Triangle have three sides and three angles. (These are called element of triangle)
- The sum of all angles of a \[\Delta \] is \[180{}^\circ \]\[\angle A+\angle B+\angle C=180{}^\circ \]
Classification of triangles according to the side
1. Equilateral triangle:
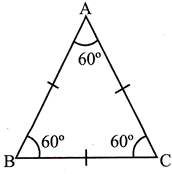
- A triangle whose sides are equal in length is called an 'equilateral triangle'.
- \[AB=BC=AC\]
- All angle are equal.
\[\angle A=\angle B=\angle C=60{}^\circ \]
2. Isosceles triangle:
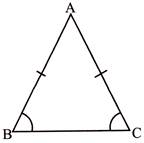
- A triangle in which two sides are equal in length is called an isosceles triangle.
- \[AB=BC\]and \[\angle B=\angle C\]
- BC is called base and \[\angle B\] and \[\angle C\] are called base angles.
3. Scalene triangle:
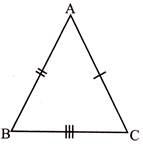
- If no two sides of a triangle are equal in length, it is called a scalene triangle.
- \[AB\ne BC\ne AC\]
Classification of triangles according to the angles
1. Acute angled triangle: If each angle of a triangle is an acute angle, men it is called an
Acute' angled triangle.
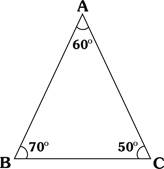
- Measure of each angle is less than 90°.
2. Right angled triangle:
A triangle in which one of its angles is a right angle is called a 'Right angled triangle'.
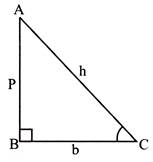
- \[\angle B=90{}^\circ \]
- The opposite side of the right angle is called Hypotenuse.
- \[A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\](Pythagoras theorem)
3. Obtuse angled triangle:
A triangle containing an obtuse angle is called an obtuse angled triangle.
Median
A line segment in which joins a vertex of a triangle to the mid-point of the opposite side is called a median.
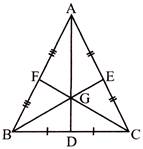
- AD, BE and FC are called medians.
- Point of intersection of the medians is called centroid. It is denoted by G.
- 'G' divide AD in the ratio \[2:1\]from the vertex side.
Quadrilateral
A closed figure bounded by four line segments is called a quadrilateral.
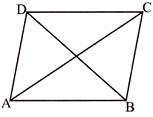
- AB, BC, CD and AD are four sides of ABCD quadrilateral.
- \[\angle A,\,\,\angle B,\,\,\angle C\]and \[\angle D\] are four angles of the quadrilateral.
- The quadrilateral has two diagonals (AC and BD).
- (AB, BC), (BC, CD), (CD, AD), (AD, AB) are four pairs of adjacent sides.
- \[(\angle A,\,\,\angle B),\] \[(\angle B,\,\,\angle C),\] \[(\angle C,\,\,\angle D),\] \[(\angle D,\,\,\angle A)\] are four pairs of adjacent angles.
- The sum of all angles of a quadrilateral is\[360{}^\circ \].
Types of Quadrilateral
- Trapezium: A quadrilateral having only one pair of parallel sides.
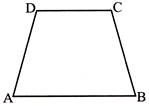
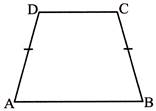
- Isosceles trapezium: A trapezium in which non - parallel sides are equal.
- Parallelogram: A quadrilateral having both pairs of opposite sides parallel and equal.
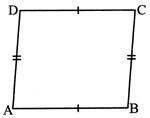
- \[AB||CD\]and \[AD||BC\]
- \[AB=CD\]and \[AD=BC\]
- \[\angle A=\angle C\]and \[\angle B=\angle D\]
- Rhombus: A parallelogram in which all sides are equal.
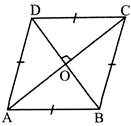
- \[AB||CD\]and \[AD||BC\]
- \[AB=BC=CD=AD\]
- Diagonals are perpendicular to each other.
- \[AO=CO\]and \[BO=DO\] (i.e. diagonals bisect each other)
- Rectangle: A parallelogram in which each angle is equal to\[90{}^\circ .\]
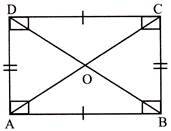
- \[AB||CD\]and \[AD||BC\]
- \[AB=CD\]and \[AD=BC\]
- \[\angle A=\angle B=\angle C=\angle D=90{}^\circ \]
- Diagonals are equal \[AC=BD\]
- \[~OA=OC=OD=OB\]
- Square: A rectangle in which whose all sides are equal.
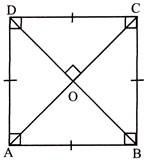
- \[AB||CD\]and \[AD||BC\]
- \[AB=BC=CD=AD\]
- \[\angle A=\angle B=\angle C=\angle D=90{}^\circ \]
- Diagonals bisect each other at\[90{}^\circ \].
- \[AC=BD\]
- Kite: A quadrilateral having two pairs of equal adjacent sides but unequal opposite sides is called a kite.
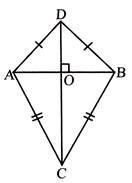
- \[AD=DB\]and \[AC=BC\]
- Diagonals are perpendicular to each other.
- \[\angle A=\angle B\]
- \[OA=OB\]
- Circle: A circle is a set of points in a plane whose distance from a fixed point is constant.
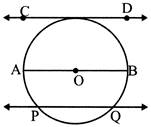
- O is called center.
- OA and OB are radius.
- AB is called diameter.
- Diameter \[=2\times \] Radius
- Diameter is the longest chord of circle.
- CD is called tangent of circle.
- PQ is called secant of a circle.

![]()
![]()
![]()
![]()





![]()











![]()





















