Geometry and Symmetry
Category : 6th Class
Geometry and Symmetry
Basic Geometrical Shapes
Lines and angles are the main geometrical concept and every geometrical figure is made up of lines and angles. Triangles are also constructed by using lines and angles.
Point
A geometrical figure which indicates position but not the dimension is called a point. A point does not have length, breadth and height. A point is a fine dot. P is a point on a plane of paper as shown below.
![]()
Line
A set of points which can be extended infinitely in both directions is called a line.
![]()
Line Segment
A line of fix length is called a line segment.
![]()
In the above figure RS is a line segment and the length of RS is fixed.
Ray
A ray is defined as the line that can be extended infinitely in one direction.
![]()
In the above figure AB can be extended towards the direction of B. Hence, called a ray.
Note: A line segment has two end points, a ray has only one end point and a line has no end points.
Angle
Angle is formed between two rays which have a common point.
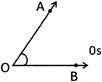
Vertex or common end point is O.
OA and OB are the arms of \[\angle AOB\]
The name of the above angle can be given as \[\angle AOB\]or \[\angle BOA\]
The unit of measurement of an angle is degree\[({}^\circ )\]
Types of Angles
Acute Angle
The angle between \[0{}^\circ \] and \[90{}^\circ \] is called an acute angle.
For example, \[10{}^\circ ,\,\,30{}^\circ ,\,\,60{}^\circ ,\,\,80{}^\circ \]are acute angles.
Right Angle
An angle of measure \[90{}^\circ \] is called a right angle.
Obtuse Angle
An angle whose measure is between \[90{}^\circ \] and \[180{}^\circ \] is called an obtuse angle.
Straight Angle
An angle whose measure is \[180{}^\circ \,\,\text{is}\]called a straight angle.
![]()
Reflex Angle
An angle whose measure is more than \[180{}^\circ \] and less than \[360{}^\circ \]is called a reflex angle.
Complementary Angle
Two angles whose sum is \[90{}^\circ \,\,\text{is}\] called the complimentary angle.
Complementary angle of any angle \[\theta \] is\[90{}^\circ -\theta \].
Supplementary Angle
Two angles whose sum is \[180{}^\circ \,\,\text{is}\] called supplementary angles.
Supplementary angle of any angle \[\theta \] is\[180{}^\circ -\theta \].
Adjacent Angle
Two angles are said to be adjacent if they have a common vertex and one common arm. In the following figure \[\angle AOC\] and \[\angle COB\]are adjacent angles.
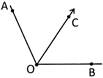
Vertically Opposite Angles
Two angles are said to be vertically opposite angles if they are formed at the intersecting point of two lines.
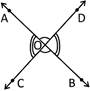
In the figure given above, \[\angle AOD\]and \[\angle BOC\] are vertically opposite angles. They are formed by intersection of AB and CD.
Similarly, \[\angle AOC\]and \[\angle BOD\] are vertically opposite angles.
Pair of vertically opposite angles are always equal.
Symmetry
In our day to day life we come across so many things around us which seems to be divided into two equal halves and both the halves look like in exact correspondence or position along an imaginary line. Take a look at the following figures

If we fold these figures along an imaginary line, we will find that both the halves are mirror images of each other. The very common term used in our day to day life for these type of figures is "symmetry". So, symmetry occurs when one shape becomes exactly the same or both the figures overlap each other. Such types of figures are called symmetrical figures.
Line of symmetry
Line of symmetry is a line that divides a figure into two identical parts, each of which is the mirror image of the other. In the above figures the imaginary line is known as the line of symmetry, so the line of symmetry is the imaginary line along which we can fold the figures so that both the halves coincide each other.
Note:
Example:
Which of the following figures does not have any line of symmetry?
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
(e) None of these
Answer (d)
Explanation: Option (d) does not have any line of symmetry as no imaginary line can be drawn in this figure to divide it into two equal halves.
Example: How many line(s) of symmetry does a regular octagon can have?
Solution: A regular octagon have 8 lines of symmetry, which is shown below
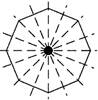
You need to login to perform this action.
You will be redirected in
3 sec
