6th Class Mathematics Fractions Operations on Fractions

   Operations on Fractions

 

In the ratio form of a fractional number, numerator is called dividend and denominator is divisor. Therefore, \[6\div 3\] is expressed in the form of fraction and written as \[\frac{6}{3}\].

 

\[\frac{6}{3}\]is not in full simplified or reduced form therefore, by division it can be simplified and the quotient of the division is the full simplified form of the fraction. Let us consider an example of fraction\[\frac{24}{36}.\] The numerator of the given fraction is not divisible by denominator but a common divisor is there between both the numerator and denominator of the fractions. Therefore, its simplified form \[\frac{2}{3}\]is the solution   of the fraction. The simplified form of the fraction is called reduced form of the fraction. 

 

 

In the following picture, some parts of picture are shaded but some are not. Find the part of the un shaded portion of the picture.

 

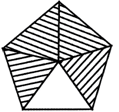
(a)\[\frac{2}{3}\]                             

(b)\[\frac{1}{5}\]

(c)\[\frac{3}{5}\]                             

(d) All of these                   

(e) None of these                                        

 

Answer: (b)         

Explanation

One part of the picture is not shaded but 4 parts are shaded.      

 

 

Proper Fractions

A fraction which has greater denominator than numerator is called proper fraction. \[\frac{3}{5},\frac{1}{2},\frac{7}{9}\] are proper fractions.  

 

 

Choose the proper fraction from the following options:

(a)\[\frac{7}{9}\]                             

(b)\[\frac{102}{34}\]

(c)\[\frac{11}{34}\]                         

(d) All of these

(e) None of these  

 

Answer: (c)  

Explanation

The fraction which has smaller numerator than denominator is called proper fraction.  

 

 

Improper Fractions

A fraction is called improper fraction even if:

1. It has smaller denominator than numerator

2. It has equal numerator and denominator                              

\[\frac{6}{5},\frac{5}{2},\frac{109}{34},\frac{6}{6}\]are improper fractions. 

 

 

Choose the improper fraction from the following options:

(a)\[\frac{56}{3}\]                           

(b)\[\frac{2}{3}\]                

(c)\[\frac{25}{43}\]                         

(d) All of these

(e) None of these  

 

Answer: (a)

Explanation

The fraction which has greater numerator than denominator is called improper fraction.  

 

 

Mixed Fractions

The combination of a fraction and a whole number is called mixed fractions. Every mixed fraction can be simplified into an improper fraction, i.e. \[5\frac{2}{7}.\]

The simplified form of a mixed fraction is always an improper fraction.      

 

 

The solution of an expression is \[4\frac{1}{2}.\] which one of the following is correct about the common name of the solution of the expression?

(a) Mixed fraction                           

(b) Proper fraction

(c) Improper fraction                     

(d) All of these

(e) None of these

 

Answer: (a)

Explanation

\[4\frac{1}{2}\]is a mixed fraction.  

 

 

Conversion of Mixed Fraction

Let us consider a mixed fraction \[4\frac{1}{2}\]. it is converted into fraction by multiplying denominator to whole and the result of multiplication is added to the numerator of the fraction. The denominator of the resulting fraction is same as the denominator of the mixed fraction. Therefore, the mixed fraction \[4\frac{1}{2}\] is written into fraction as\[\frac{14}{3}.\]

Therefore,

\[\text{Fraction =}\frac{\text{Denominator of mixed fraction  }\!\!\times\!\!\text{  Whole) + Numerator}}{\text{Denominator of the mixed fraction}}\]      

 

 

The fraction, \[\frac{34}{3}\] is equivalent of which one of the following fractions?

(a)\[12\frac{1}{3}\]                        

(b)\[13\frac{1}{3}\]

(c)\[11\frac{1}{3}\]                         

(d) All of these

(e) None of these  

 

Answer: (c)                

Explanation

\[\frac{34}{3}=11\frac{1}{3}\]  

 

 

Conversion of Improper Fraction into Mixed Fraction  

Let us consider an improper fraction \[\frac{13}{3}.\]

The following steps are used to obtain the mixed fraction of the above given fraction:

Step 1:   Divide the numerator by denominator \[3\overset{4}{\overline{\left){\begin{align}   & 13 \\  & \frac{12}{1}. \\ \end{align}}\right.}}\]

Step 2:   Required mixed fraction. \[\text{= Quotient}\frac{\text{Remainder}}{\text{Divisor}}\text{=4}\frac{\text{1}}{\text{3}}\text{.}\]  

 

 

Add the following shaded parts of the pictures and express the result into its mixed fraction:

 

 

 

(a)\[2\frac{1}{2}\]                           

(b)\[1\frac{1}{2}\]

(c)\[1\frac{3}{2}\]                           

(d) All of these

(e) None of these                          

 

Answer: (b)                

Explanation  

\[1+\frac{1}{2}=\frac{3}{2}=1\frac{1}{2}\]

 

 

Equivalent Fractions

When numerator and denominator of a fraction is multiplied by same number, its equivalent fraction is obtained.

By multiplying with a common number 12to the numerator and denominator of the fraction \[\frac{2}{3}.\frac{2\times 12}{3\times 12},\] we obtain its equivalent fraction \[\frac{24}{36}.\]

Another equivalent fraction of \[\frac{2}{3}\] is obtained by multiplying common number, 13 to the numerator and denominator, \[\frac{2}{3}\times \frac{13}{13}=\frac{26}{39}.\]

The reduced form of the fraction, \[\frac{48}{72}\] is obtained on dividing by its common divisor. \[\frac{48}{72}\]can be divided by its common divisor, 24, therefore, reduced fraction of the fraction, \[\frac{48}{72}\]is \[\frac{2}{3}.\]      

 

 

The fraction, \[\frac{5}{2}\] can also be written by which one of the following options?

(a)\[\frac{1}{2}\times 2\]                            

(b)\[2\div \frac{1}{2}\]

(c)\[\frac{1}{2}+2\]                        

(d)\[2-\frac{1}{2}\]

(e) None of these  

 

Answer: (c)                

Explanation

\[\frac{1}{2}+2=2\frac{1}{2}=\frac{5}{2}\]    

 

 

Fractions in its Lowest Term

The lowest term of a fraction is obtained when HCF of the numerator and denominator is not other than 1.

Let a fraction is \[\frac{45}{25},\] the HCF of its numerator and denominator is 5, therefore, it can be expressed into its lowest term on dividing the fraction by its HCF. Therefore, \[\frac{45\div 5}{25\div 5}=\frac{9}{5},\] the lowest term of \[\frac{45}{25}\] is \[\frac{9}{5}.\]    

 

 

 

The lowest term of a fraction is obtained when HCF of its numerator and denominator is 2. Find the lowest term of \[\frac{102}{46}.\]

(a)\[\frac{2}{3}\]                             

(b)\[\frac{52}{21}\]

(c)\[\frac{51}{23}\]                         

(d) All of these

(e) None of these  

 

Answer: (b)

Explanation

HCF of numerator and denominator is 2, dividing by 2,we get \[\frac{52}{21}.\]  

 

 

Like and Unlike Fractions

When two or more fractions have same denominator then they are called like fractions while unlike fractions do not have equal denominators.

The fractions, \[\frac{5}{2},\frac{7}{2},\frac{23}{2}\] are like fractions and \[\frac{6}{7},\frac{7}{2},\frac{1}{7}\]are unlike fractions.  

 

 

Choose the group of unlike fractions from the following groups of fractions:                

(a)\[\frac{3}{2},\frac{9}{2},\frac{5}{2}\]                

(b)\[\frac{5}{2},\frac{9}{4},\frac{1}{7}\]

(c) \[\frac{3}{3},\frac{9}{3},\frac{5}{3}\]                

(d) All of these

(e) None of these  

 

Answer: (b)  

Explanation

The fractions \[\frac{5}{2},\frac{9}{4},\frac{1}{7}\]having unequal denominators. Hence, this is the group of unlike fractions.  

 

 

Comparison of Fractions

When two or more fractions are given then greater and smaller fractions can be obtained by comparing its numerators and denominators.

 

 

Comparison of Like Fractions

Comparison of two fractions which have same denominator or like fractions is obtained on comparing its numerators, in other words, if two or more fractions have equal denominators then the greater fraction has greater numerator and smaller has smaller.

Fractions \[\frac{3}{4}\] and \[\frac{9}{4}\] have same denominator, therefore, those having greater numerator \[\left( \frac{9}{4} \right)\]is greater than other \[\left( \frac{3}{4} \right).\]

If two or more fractions have equal numerators but different denominators then those having greater numerator is greater than other fraction.    

 

 

Find the smallest fraction from the following fractions, \[\frac{1}{2},\frac{3}{2},\frac{4}{2}.\]

(a)\[\frac{4}{2}\]                             

(b)\[\frac{1}{2}\]

(c)\[\frac{3}{2}\]                             

(d) All of these                 

(e) None of these  

 

Answer: (b)

Explanation

The denominators of the fractions are equal thus the smaller has smaller numerator.  

 

 

Comparison of Unlike Fractions

Two or more unlike fractions are compared by comparing its equivalent fractions with same denominators. The following steps are used to compare two or more unlike fractions:

Step 1:   Find the LCM of denominators of the fractions.

Step 2:   Convert the denominator equal to the LCM by multiplying with same number to those, which do not have denominator equal to the LCM.

Step 3:   Now compare the fractions in this way that the greater fraction has greater numerator.

Let two unlike fractions, \[\frac{3}{4},\frac{9}{2}\] are compared as follows,

The LCM of both the denominators is 4. Fraction, \[\frac{3}{4}\] has denominator as same as the LCM but the fraction \[\frac{9}{2}\] has different denominators, so it should be multiplied by 2. \[\frac{9}{2}\times \frac{2}{2}=\frac{18}{4},\]now both the fractions \[\frac{3}{4},\frac{18}{4}\] have equal denominators, therefore,\[\frac{18}{4}=\frac{9}{2}\]is greater than , because it has greater numerator.

 

 

Find the biggest fraction from the following fractions, \[\frac{7}{9},\frac{3}{7},\frac{5}{3}.\]

(a)\[\frac{9}{7}\]                             

(b)\[\frac{3}{7}\]

(c)\[\frac{5}{3}\]                             

(d) All of these                 

(e) None of these

Answer: (c)

Explanation

The LCM of the fractions is 63, therefore, given fractions are converted into its equivalent fractions in such a way that their denominators should be equal. Therefore, \[\frac{7}{9}\times \frac{7}{7}=\frac{49}{63},\frac{3}{7}\times \frac{9}{9}=\frac{27}{63}\]and\[\frac{5}{3}\times \frac{21}{21}=\frac{105}{63}\]thus the equivalent fractions of the given fractions are \[\frac{49}{63},\frac{27}{63},\frac{105}{63}\]respectively. Comparing them, we get \[\frac{105}{63}=\frac{5}{3}\] is the greatest fraction because it has greater numerator