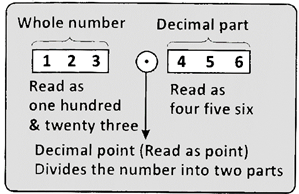
Decimals
Category : 6th Class
Decimals
e.g., 5.8, 19.63, 7.269, 0.058, etc.,
(i) Whole-number part and (ii) Decimal part
These parts are separated by a dot (.) called the decimal point.
e.g., Write 236.784 in place value chart.
|
100 |
10 |
1 |
0.1 |
0.01 |
0.001 |
|
Hundreds |
Tens |
Ones |
Tenths |
Hundredths |
Thousandths
|
|
2 |
3 |
6 |
7 |
8 |
4 |
0.6 lies between 0 and 1.
0.6 is 6 tenths.
So, divide the unit length between 0 and 1 into 10 equal parts & take 6 parts as shown.

e.g., 5.39 has two decimal places and 9.368 has three decimal places.
e.g., 9.82, 5.03, 13.85 etc.,
e.g, 3.4, 5.98, 111.035 etc.,
Note: Adding and number Zeros to the extreme right of the decimal part of a decimal number does not change its value.
e.g., 2.64 = 2.640 = 2.6400 etc.
Step 1 : Convert the given decimal numbers into like decimals.
Step 2 : First compare the whole-number part.
The decimal number with the greater whole number part is greater.
Step 3: If the whole number parts are equal, compare the tenths digit. The decimal number with the greater digit in the tenths place is greater.
Step 4: If the tenths digits are also equal, compare the hundredths digits, and so on.
e.g., (i) 63.87 > 59.87
(ii) 24.85 > 24.65
(iii) 111.035 < 111.038
Express 2.35 as a fraction.
Step 1: In the numerator, write the given decimal number without the decimal point.
\[2.\underset{\leftarrow }{\mathop{35}}\,=\frac{(235)}{(\,\,\,\,\,)}\]
Step 2: From 'right to left' count the number of decimal places, say 'x'.
Here x = 2.
Step 3: In the denominator, write 1 followed by 'x' number of zeros.
\[2.35=\frac{235}{100}\]
Step 4: Simplify the obtained fraction into its lowest terms.
(i) Conversion of decimal fraction to decimal.
Express \[\frac{17153}{1000}\]as a decimal.
Step 1: Write the numerator as it is 17153.
Step 2: Count the number of zeros in the denominator. Let it be 'x'.
Here x = 3.
\[\therefore \frac{17153}{1000}=17.153\]
(ii) Conversion of a non-decimal fraction into a decimal.
Express\[\frac{318}{7}\] as a decimal.
Step 1: Divide the number as usual.
Step 2: If dividend is less than divisor, place the decimal point in quotient.
Step 3: Place a zero in the dividend.
Step 4: Repeat the division process till remainder is zero or as per the required number of decimal places.
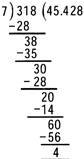
Note: (a) Express \[\frac{\mathbf{318}}{\mathbf{7}}\]as a decimal (Upto 3 Decimals \[\frac{\mathbf{318}}{\mathbf{7}}\mathbf{=45}\mathbf{.428}\]
(b) Express \[\frac{\mathbf{318}}{\mathbf{7}}\]as a decimal (upto 2 decimal)\[\frac{\mathbf{318}}{\mathbf{7}}\mathbf{=45}\mathbf{.42}\]
(c)Express \[\frac{\mathbf{318}}{\mathbf{7}}\]as a decimal correct to 2 decima; places \[\frac{\mathbf{318}}{\mathbf{7}}\mathbf{=45}\mathbf{.43}\](2 is rounded off to 3 as the third decimal digit is 8 which is greater than 5.)
e.g., Add: 27.8, 46,175.09 and 685.7.
Step 1: Convert the given decimals into like decimals. 27.80, 46.00, 175.09 and 685.70.
Step 2: Write the addends one below the other in column form, keeping the decimal points of all the addends in the same column and the digits of the same place in the same column.
Step 3: Add as in the case of whole numbers.
Step 4: In the sum, place the decimal point directly under decimal points in the addends.

Hence, 934.59 is the sum of the given decimals.
e.g., Subtract 35.87 from 63.2.
Step1: Convert the given decimals into like decimals.
Step 2: Write the smaller number below the larger one in column form in such a way that the decimal points of both the numbers are in the same column and the digits of the same place lie in the same column.
Step 3: Subtract as in the case of whole numbers.
Step 4: In the difference, place the decimal point directly under the decimal points of the given numbers.
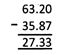
Hence, 27.33 is the difference of the given decimals.
1 mm = \[\frac{1}{10}\]of a centimeter
i.e., 1 mm = 0.1 cm; 1 cm = 0.01 m
100 cm = 1 m
1000 mm = 1m
1000 m=1km
1000 m\[l\]=1 liter
1000\[l\]=1 k\[l\]
1000 mg=1g
1000 g=1kg
You need to login to perform this action.
You will be redirected in
3 sec
