6th Class Mathematics Fractions Fractions and Decimals

FRACTIONS AND DECIMALS

 

FUNDAMENTALS

Natural numbers: All counting numbers are called natural numbers.

•                   It is denoted by N.
•                  \[N=\left\{ 1,2,3,4,\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \right\}\]

Whole number: Natural numbers together with zero are called whole numbers.

•                  It is denoted by W.
•                  \[~W=\left\{ 0,1,2,3,\_\_\_\_\_\_\_\_\_\_ \right\}\]
•                 Fraction: A part of whole is called fraction.

or

A number written in the form \[\frac{x}{y},\] where \[x\] and \[y\] are whole numbers and \[y\ne 0\] is called fraction,

•                  \[\frac{x\to \text{Numerator}}{y\to \text{Denominator}}\]

 

Types of Fraction                                      

•                  Decimal fraction: A fraction whose denominator is 10, 100, 1000 etc.......is called a decimal fraction.

Example: \[\frac{1}{10},\frac{2}{100},\frac{5}{1000}\]etc...

•                  Vulgar fraction: A fraction whose denominator is a whole number, other then 10, 100, 1000 etc.......  is called a vulgar fraction.
•                  Proper fraction: A fraction in which numerator is less than the denominator is called a proper fraction.

Example: \[\frac{1}{2},\frac{3}{4},\frac{7}{9}\]etc...

•                   Improper fraction: A fraction in which numerator is greater than the denominator is called an improper fraction.

Example: \[\frac{7}{2},\frac{9}{4},\frac{11}{10}\] etc...

•                  Mixed fraction (compound fraction): The combination of whole number with proper fraction is called a mixed fraction.

Example: \[1\frac{1}{2},7\frac{3}{4},2\frac{1}{2}\]etc...

•                  Equivalent Fractions: Fractions that represent the same part are called equivalent fractions.

Example: \[\frac{1}{2}\] and \[\frac{2}{4},\,\,\frac{1}{4}\,\,\text{and}\]\[\frac{4}{16},\,\,\frac{10}{12}\,\,\text{and}\]\[\frac{5}{6}\]

•                  Like fractions: Fractions that represent the same denominators are called like fractions.

Example: \[\frac{4}{5}\]and \[\frac{2}{5},\,\,\frac{2}{7},\,\,\frac{3}{5},\,\,\frac{5}{7}\]etc...

•                  Unlike fractions: Fractions that have different denominators are called unlike fractions.
•                  Unit fractions: Fractions which have one as numerator are called as unit fractions.
•                  Complex fractions: A fraction whose one or both the terms are fractions is called a complex fraction.

 

Companion of fractions

•                  If two fractions \[\frac{x}{y}\]and \[\frac{z}{w}\] are to be compared, we cross multiply

(i)     If\[x\times w>y\times z\], then \[\frac{x}{y}>\frac{z}{w}\]

(ii)    If\[x\times w<y\times z\], then \[\frac{x}{y}<\frac{z}{w}\]

(iii)    If\[x\times w=y\times z\], then\[\frac{x}{y}=\frac{z}{w}\]

Example: Compare the \[\frac{2}{3}\] and \[\frac{5}{6}\]

Solution: On cross multiplication we get, \[2\times 6=12\]and \[3\times 5=15\]

\[12<15\]

\[\therefore \]            \[\frac{2}{3}<\frac{5}{6}\]

Example: Arrange \[\frac{2}{5},\,\,\frac{1}{4},\,\,\frac{3}{2},\,\,\frac{9}{10}\]in ascending order.

Solution: The LCM of \[5,\,\,4,\,\,2,\,\,10=20\]

\[\frac{2}{5}=\frac{2\times 4}{5\times 4}=\frac{8}{20},\frac{1}{4}=\frac{1\times 5}{4\times 5}=\frac{5}{20},\frac{3}{2}=\frac{3\times 10}{2\times 10}=\frac{30}{20}.,\]

\[\frac{9}{10}=\frac{9\times 2}{10\times 2}=\frac{18}{20}\]

Now, compare the numerators of like fractions \[\frac{8}{20},\frac{5}{20},\frac{30}{20},\frac{18}{20}\]

Arrange them in ascending order, we get \[\frac{5}{20}<\frac{8}{20}<\frac{18}{20}<\frac{30}{20}\]

Hence, \[\frac{1}{4}<\frac{2}{5}<\frac{9}{10}<\frac{3}{2}\]

 

Finding fraction between two given fraction

•                 If \[\frac{w}{x}\]and \[\frac{y}{z}\] are two fractions, the fraction lying between them is \[\frac{w+y}{x+z}\]then \[\frac{w}{x},\,\,\frac{w+y}{x+z},\,\frac{y}{z}\]

Example: Find a fraction lying between \[\frac{2}{3}\] and\[\frac{5}{7}\]

Solution: We have \[\frac{2}{3}\]and \[\frac{5}{7}\]

Fraction lying between \[\frac{2}{3}\] and \[\frac{5}{7}\] is \[\frac{2+5}{3+7}=\frac{7}{10}\]

So, we have \[\frac{2}{3},\frac{7}{10},\frac{5}{7}.\]

 

Fundamental operations on fraction

•                   Addition: \[\frac{x}{y}+\frac{z}{y}=\frac{x+z}{y}\]

Example: Add\[\frac{3}{7}+\frac{5}{7}=\frac{3+5}{7}=\frac{8}{7}\]

Note: While adding unlike terms, first convert them into like fractions and then add as like fractions.

 

Properties of Addition of fraction

(i) Closure property: If \[\frac{x}{y}\] and \[\frac{z}{w}\] are two fractions, then \[\frac{xw+zy}{yw}\] is also a fractions

(ii) Commutative property: If \[\frac{x}{y}\] and \[\frac{z}{w}\] are two fractions, them\[\frac{x}{y}+\frac{z}{w}=\frac{z}{w}+\frac{x}{y}\]

(iii) Associative property: If \[\frac{r}{s},\]\[\frac{t}{u}\] and \[\frac{v}{w}\] are three fractions, then \[\frac{r}{s}+\left( \frac{t}{u}+\frac{v}{w} \right)=\left( \frac{r}{s}+\frac{t}{u} \right)+\frac{v}{w}\] Subtraction  \[\frac{x}{y}-\frac{z}{y}=\frac{x-z}{y}\]

Example: \[\frac{4}{5}-\frac{3}{5}=\frac{4-3}{5}=\frac{1}{5}\]

Note: While subtracting unlike fraction, first convert them into like fractions and find difference as in like fractions.

 

Multiplication

•                 If \[\frac{x}{y}\] and \[\frac{z}{w}\] are two fractions, then the product of these fraction \[=\frac{x\times z}{y\times w}=\frac{\text{Product of numerators}}{\text{Product of denominators}}\]

Example: Multiply \[\frac{3}{7}\] and \[\frac{2}{5}\]

Solution: \[\frac{3}{7}\times \frac{2}{5}=\frac{3\times 2}{7\times 5}=\frac{6}{35}\]

 

Properties of multiplication of fractions

•                Commutative property: If \[\frac{x}{y}\] and  \[\frac{z}{w}\] are two fractions then \[\frac{x}{y}\times \frac{z}{w}=\frac{z}{w}\times \frac{x}{y}\]
•                        Associative property: If \[\frac{r}{s},\] \[\frac{t}{u}\] and \[\frac{v}{w}\] are three fractions, then

\[\frac{r}{s}\times \left( \frac{t}{u}\times \frac{v}{w} \right)=\left( \frac{r}{s}\times \frac{t}{u} \right)\times \frac{v}{w}\]

•                   Reciprocal of fraction: If \[\frac{x}{y}(y+0)\] is a fraction, then the reciprocal of this non-zero fraction is\[\frac{y}{x}\].

Example: Find the reciprocal of\[\frac{5}{7}\].

Solution: The reciprocal of \[\frac{5}{7}\] is\[\frac{7}{5}\].

•                   Division: It \[\frac{x}{y}\] and \[\frac{w}{z}\] are two fractions, then\[\frac{x}{y}\div \frac{w}{z}=\frac{x}{y}\times \frac{z}{w}\]

Example: Divide\[\frac{5}{9}\div \frac{25}{3}\]

Solution: \[\frac{5}{9}\div \frac{25}{3}=\frac{5}{9}\times \frac{3}{25}=\frac{1}{15}\]

•                   Decimals: The word "Decimal" really means "based" on "10" (from latin decimal: a tenth part).

Example: \[0.6,\,\,1.76,\,\,5.046\]

 

•                 A decimal number has two parts, separated by a decimal point. Left part of the decimal point is whole number and right of the decimal is decimal part.

 

Look at this Example

                 

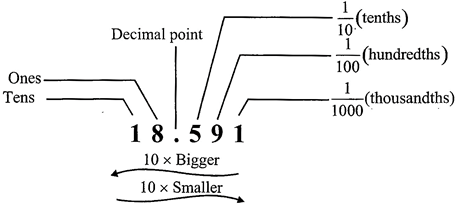
Example:     Study the expanded form of the given decimal numbers:

 

Decimal Number	Tens	Units	Tenths	Hundredths	Thousandths
\[35.6\]	3 tens	5 units	6 tenths
\[25.58\]	2 tens	5 units	5 tenths	8 hundredths
\[17.415\]	1 ten	7 units	4 tenths	1 hundredths	5 thousandths
\[78.004\]	7 tens	8 units	0 tenths	0 hundredths	4 thousandths
\[06.07\]	0 tens	6 units	0 tenths	7 hundredths

 

Types of Decimals

•                  Like decimals: Decimals having the same number of decimal places are called like decimals.

Example: (i) \[0.7,\,\,1.1,\,\,25.6,\,\,238.4~\]        (ii) \[0.21,\,\,666.26,\,\,6.57\]

•                  Unlike decimals: Decimals with different number of decimal places are unlike decimals.

Example: (i) \[0.7,\,\,0.21,\,\,6.323\]                    (ii) \[5.17,\,\,9.2,\,\,16.276\]

 

Converting unlike decimals into like decimals

Example: To convert \[2.5,\,\,8.03\]and \[7.352\] into like decimals.

Solution: We have to convert \[2.5\]and \[8.03\] into equivalent decimals with three decimal places i.e., \[2.5=2.500,\,\,8.03=8.030,\]

Now\[2.500,\,\,8.030,\,\,7.352\]like decimals.

 

Operations on Decimals

1.            Addition of Decimals:

Example: (i)   Add \[6.3\]and \[5.75\]

 Convert to like decimals

(ii)  Add \[6.5,\,\,7.05\] and \[5.325\]

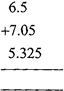 Convert to like decimals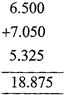

 

2.            Subtraction of Decimals:

Example: Subtract \[56.128\]from \[68.75\]

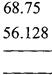 convert to like decimals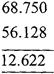

3.            Multiplication of decimals:

In multiplying the decimals,

(a) Multiply as with whole numbers ignoring the decimals.

(b) Count the number of decimal places in factors.

(c) Show the number of decimal places in the product as many as there are in the factors.

(d) While counting the digits in the product to place the decimal point, start from the right.

Step-1:

Example:    

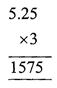
Step-2:

Total number of decimal places in the factors are 2

 

•                   Zero in the product:

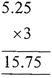
Care - 1: Some time you need to write extra zeros in the product on the left side to be able to show the correct number of decimal places.

Example: Multiply \[0.2\]by \[0.2\]

Here, number of decimal places are 2

Extra zero is required to show two decimal places.

Case - 2: Multiplication by 10,100 and 1000.

•                  Multiplying by 10 moves the decimal point one place to the right.

Example: \[10\times 0.389=03.89\]

•                  Multiplying by 100 moves the decimal point two places to the right.

Example:\[100\times 0.785=78.5\]

•                  Multiplying by 1000 moves the decimal point three places to the right.

Example: \[1000\times 1.3\text{ }95=1395\]

 

DIVISION OF DECIMAL

Case - 1: Dividing by whole number

•                Dividing by decimals is just like dividing whole numbers ignoring the decimal point. Place the decimal point in the quotient directly above the decimal point, when you divide decimals, the remainder is further divided by placing extra zeros to complete the division (that is till the remainder is zero).

Example:

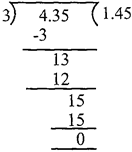
Hence \[4.35-3=1.45\]

Case - 2: Division by 10, 100, 1000

1.            On division by 10 the decimal point moves one decimal place to the left.

Example:          (i) \[4-10=0.4\]                          

(ii) \[321.4-10=32.14\]

2.            On division by 100 the decimal point moves two decimal places to the left.

Example:          (i) \[321.5-100=3.215\]              

(ii) \[244-100=2.44\]

3.            On division by 1000 the decimal point moves three places to the left.

Example:          (i) \[321.6-1000=0.3216\]                       

(ii) \[3.25-1000=0.0325\]

 

Note: You need to place extra zeros wherever necessary.

Case - 3: Division by a decimal fraction

When we divide a decimal fraction by another decimal fraction we have to first change the divisor into a whole number.\[0.76\div 0.4=?\]

Step - 1: Make the decimal places of the dividend and divisor equal that is \[\frac{0.76}{0.4}=\frac{0.76}{0.40}\]

Step - 2: Now remove decimal point as the decimal places are equal. \[\frac{0.76}{0.4}=\frac{0.76}{0.40}=\frac{76}{40}\]

Step - 3: Now divide 76 by 40 as usual and write the answer.

\[\therefore \]\[0.76\div 0.4=1.9\]

Note: To convert the decimal divisor into a whole number multiply it with either 10 or 100 or 1000 and so on according to the decimal places.