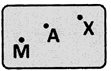Basic Geometrical Ideas
- Point: A dot marked on a paper with the sharp tip of a pencil is called a point.
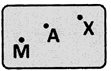
- A point is denoted by a single capital letter such as A, B, C etc. A point has only a position.
- Line: A countless number of points placed closely form a line. It extends indefinitely on both sides.
Two points on a line determine it. A line is denoted as\[\overleftrightarrow{~AB}\].
- Line segment: If A and B are two points on a line, the part AB of the line is called the line segment AB, denoted as\[\overline{AB}\]. It has 2 end points - A and B. Sometimes a line is denoted by small case letters such as /, m etc.
- The line AB (\[\overleftrightarrow{AB}\]) is the same as the line BA (\[\overleftrightarrow{BA}\] ). The line segment AB is same as the line segment BA.
Two line segments \[\overline{AB}\]and \[\overline{CD}\]are said to be congruent if they are of equal length.
- Ray: The part of a line that extends indefinitely in one direction from a given point 0 is called a ray. A ray has only one end point, 0. Ray \[\overline{OA}\]is denoted as o/T. It extends in the direction of A.
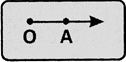
- \[\overleftrightarrow{OA}\]and \[\overleftrightarrow{AC}\] are two different rays. The first letter in the representation gives the initial point of the ray.
- A ray has no definite length, as it can be extended indefinitely in a direction.
- An unlimited number of rays can be drawn with the same initial point.
- Angle: The part of the plane between two rays with the same initial point is called an angle. The common end point is called the vertex and the two rays are called the arms of the angle. An angle is denoted with the vertex in between two points on the arms of the angle.
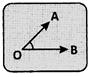
\[\therefore \]The angle shown in the figure is \[\angle \]AOB •
It is same as Z BOA (since the same part of the plane is considered between the arms of the angle).
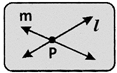
- Intersecting lines: If two lines have a common point, they are called intersecting lines. The common point is called the point of intersection.
I and m are called intersecting lines. P is called the point of intersection.
- Concurrent lines: Three or more lines having a common point are called concurrent lines. The common point is called the point of concurrence.
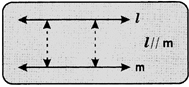
- Parallel lines: Two lines or line segments which do not intersect are called parallel lines, if the distance between them remains constant.
The symbol \['//'\] is used to denote that two lines are parallel. So, \[l\]// m is read as 7 is parallel to m'.
- Transversal: A line or line segment which intersects two or more straight lines or line segments at different points is called a transversal.
- Plane: A set of infinite number of points that extend indefinitely in all directions is called a plane.
- Collinear points: Three or more points lying on the same line are called collinear points. Points that are not collinear are called non-collinear points.
- Coplanar lines: Three or more lines lying in the same plane are palled coplanar lines. Lines that do not lie in the same plane are called non-coplanar lines.
- Triangle: A plane figure bounded by three line segments which are formed by joining three non-collinear points is called a triangle.
Three sides, three angles and three vertices are called the elements of a triangle.
Points which lie inside the triangle are said to be in the interior of the triangle.
Points which lie on the boundary of a triangle are said to be on the triangle.
Points which lie outside the triangle are said to be in the exterior of the triangle.
- The interior and the boundary of the triangle is called the triangular region.
- A circle is a plane closed figure formed by joining a set of points which are at an equal distance from a fixed point.
- The fixed point is called the centre of the circle.
- The line segment joining the centre and any point on the circle is called its radius. Plural form of radius is radii.
- A circle divides the plane into 3 parts: interior, boundary and exterior.
- The interior and the boundary of a circle is called the circular region.
- A line segment joining any two points on the circle is called a chord of the circle.
- A chord of the circle which passes through its centre is called a diameter of the circle. The diameter is the longest chord of the circle.
- The radius of a circle is half the diameter. The diameter is twice the radius.
- We can draw many diameters to a circle. All the diameters of a circle will have the same length.
- Any part on the boundary of a circle is called an arc of the circle. Symbol for arc is \[\overset\frown{\,\,\,\,\,\,\,\,}\].
- The total boundary length of a circle is called the circumference of the circle.
- The major part of the boundary of circle is called the major arc. The minor part of the boundary of circle is called the minor arc.
- The part of the circular region bounded by the major arc and the chord is called the major segment.
- The part of the circular region bounded by the minor arc and the chord is called the minor segment.
- If ah arc represents half of the circle, it is a semicircle or half-circle. The diameter of a circle divides it into two semicircles.
- The region of the circle bounded by two radii and a minor arc is called the minor sector and the region bounded by two radii and a major arc is called the major sector.
Observe the circle given.
O = centre
OA = radius
AB = diameter
\[\overset\frown{AB}\]
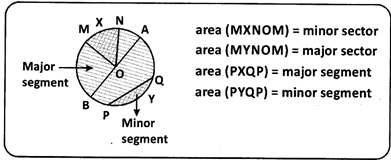
\[\overset\frown{AB}\]= minor segment
\[\overset\frown{PQ}\]= chord
arc \[\overset\frown{PYQ}\]= minor arc
arc \[\overset\frown{PXQ}\]= major arc
- The geometrical figures triangle, square, rectangle and circle are all closed plane figures or closed curves. They are bounded by line segments or curved lines.
- Closed plane figures bounded by line segments/are called polygons.
- A triangle is polygon having 3 sides.
- Squares and rectangles are polygons having four sides. All four sided polygons are named as quadrilaterals. Square, rectangle, parallelogram, rhombus and trapezium are all quadric - laterals.
- In any quadrilateral ABCD, \[\angle \]A and \[\angle \]B, \[\angle \]B and \[\angle \]C,\[\angle \]C and \[\angle \]D and \[\angle \]D and \[\angle \]A are adjacent angles. \[\angle \]A and \[\angle \]C, \[\angle \]B and Z\[\angle \]D are opposite angles.
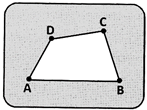
AB and BC, BC and CD, CD and DA, DA and AB are adjacent sides. AB and CD, BC and DA are opposite sides.