Reasoning and Aptitude
Category : 5th Class
Reasoning and Aptitude
Introduction
Learning process is dependent on one’s ability to think logically and reason quickly and effectively. So Reasoning and logic skills are an important part in our progress as these skills are very useful in our day to day life. In this chapter, we will learn various problems related to reasoning and aptitude.
Problems Based on Patterns
Pattern is a list of numbers or letters that follows a certain sequence of a certain rule. To solve them all we have to do is figure out the pattern and come up with the next logical number or letter of the sequence.
What is the missing number in the given series below?

(a) 18 (b) 22
(c) 16 (d) 14
(e) None of these
Answer (c)
Explanation: Pattern followed in
![]() is;
is; ![]()
Or, \[6=\frac{8}{2}+2=4+2,9=\frac{14}{2}+2=7+2,12=\frac{20}{2}+2=10+2\]
So, ? = \[\frac{28}{2}+2=14+2=16.\] Hence, missing number is 16.
Figure Pattern
Figure pattern is a collection of figures that follows a certain sequence or a certain rule.
How many shaded squares will be there in pattern 73?
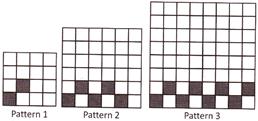
(a) 218 (b) 215
(c) 212 (d) 221
(e) None of these
Answer (a)
Explanation: Number of shaded squares in patter (1) \[=1\times 3-1=2\]
Number of shaded squares in pattern (2)
\[=2\times 3-1=5\]
Number of shaded squares in pattern (3)
\[=3\times 3-1=8\]
Therefore, the pattern followed is:
\[(1\times 3-1),(2\times 3-1),(3\times 3-1)\,..........\]
Hence, the required number of shaded squares in pattern (73)
\[=73\times 3-1=219-1=218.\]
Problems Based on Alphabet Test and Word Formation
Alphabet test is one of the most common topic of reasoning where we come across various types of problems as follow:
Find out the word which CANNOT be made from the letters of the given word.
PROGRAMMING
(a) Margin (b) Ranger
(c) Gaming (d) Roaming
(e) None of these
Answer (b)
Explanation: In the word 'Ranger' the letter 'E' is not in the word PROGRAMMIMG.
Arrange the given words as they are arranged in dictionary.
(a) 5, 4, 2, 3, 1 (b) 5, 4, 3, 1, 2
(c) 5, 3, 4, 1, 2 (d) 4, 5, 3, 1, 2
(e) None of these
Answer (b)
Explanation: Correct order of the given words as arranged in dictionary is:
Example\[\to \]Exciting \[\to \] Exclude\[\to \] Excuse\[\to \]Execute
(5) (4) (3) (1) (2)
Which of the following letters is 9th to the left of 7th letter from the right end?
ABCDEFGHIJKLMNOPQRSTUVWXYZ
(a) M (b) K
(c) L (d) N
(e) None of these
Answer (b)
Explanation: 7th letter from the right end is T and 9th to the left of T is 'K'.
Identify the one that does not belong to the group.
(a) POS (b) QPR
(c) MLN (d) UTV
(e) None of these
Answer (a)
Explanation: There are three consecutive letters in QPR, MLN and UTV but letters in POS are not consecutive.
Problems Based on Analogy and Classification
In analogy based problems, we will usually be given one pair of images that are connected in a particular way and the first image of a second pair. We have to find the correct image to complete the second pair in the same way as the first pair.
Classification of figures or shapes test our ability to work out, which shapes are similar and which are different in a given set of options. We need to use our observation skill to compare the given shapes, symbols and find the visual link or links.
There is a certain relationship between the pair of figures given on either side of :: and find the missing part.

(a) 
(b) 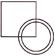
(c) 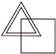
(d) 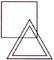
(e) None of these
Answer (d)
Explanation: The upper figure is converted into a figure similar to the lower figures and each one of the lower figures is converted to a figure similar to the upper figure.
Find the odd one out.
(a) \[\frac{12}{L}\] (b) \[\frac{9}{I}\]
(c) \[\frac{27}{Y}\] (d) \[\frac{19}{5}\]
(e) None of these
Answer (c)
Explanation: Alphabets and their position is as follow:
A\[\to \]1, B\[\to \]2, C\[\to \]3, D\[\to \]4, ................. I\[\to \]9, ………….s\[\to \]19……………. y\[\to \]![]()
Therefore, the relation given in option (c) is odd one out.
Find the figure which is different from the others.
(a) 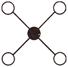 (b)
(b) 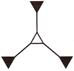
(c) 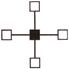 (d)
(d) 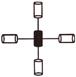
(e) None of these
Answer (b)
Explanation: Except the figure given in option (b), all other figures in options (a), (c) and (d)
And (d) have inner part shaded.
Problems Based on Geometrical Shapes
Geometrical shapes come from geometry which is the math of shapes made of points and lines. Some shapes are simple such as the triangle, square and circle, whereas other shapes are complex. While solving logical reasoning based on geometrical shapes, following: points are important:
(i) Two half rotation mean one full rotation.
(ii) \[\frac{1}{4}\] rotation means figure rotates \[90{}^\circ \] clockwise or \[90{}^\circ \] anticlockwise.
(iii) \[\frac{1}{8}\] rotations means figure rotates \[45{}^\circ \] clockwise or \[45{}^\circ \] anticlockwise.
Example:
How many lines of symmetry does the figure have?

(a) 1 (b) 2
(c) 4 (d) 0
(e) None of these
Answer (a)
Explanation: In the give figure, there are one line of symmetry.
Example:
How many triangles are there altogether in the given figure?
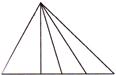
(a) 8 (b) 10
(c) 12 (d) 14
(e) None of these
Answer (b)
Explanation: Clearly, there are 10 triangles in the given figure.
Count the number of right angles inside the figure given below.
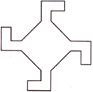
(a) 8 (b) 20
(c) 12 (d) 16
(e) None of these
Answer (c)
Explanation: Clearly, there are 12 right angles in the figure inside the figure.
You need to login to perform this action.
You will be redirected in
3 sec
