5th Class Mathematics Factors and Multiples Factor & Multiple

FACTOR AND MULTIPLE

         FUNDAMENTALS

•                   One number is said to be a factor of another when it divides the other exactly.

          Properties of Factors

•                   1 is factor of every number

Example: 

\[85=1\times 85\]

\[73=1\times ~73\]

\[10=1\times 10\] etc.

•                    Every non-zero number is a factor of itself.

Example:

\[18=18\times 1\]

\[21=21\times ~1\]

\[15=15\times ~1\] etc.

•                   Factor of a non-zero number is less than or equal to the number.

Example:

\[18=1\times 2\times 3\times 3\]  (1, 2, 3, 6, 9, 18 are factor)

\[17=1\times ~17\]           (1 and 17 are factors)

\[33=1\times ~3\times ~11\]         (1, 3, 11 and 33 are factors)

\[13=1\times ~13\] etc.     (1, 13)

•                  1 is the only number having one factor only.
•                   Every non-zero number other than 1 has at least two factors namely 1 and itself.

Example:

\[2=1\times ~2\]                        \[(1,\,\,2)\]

\[6=1\times ~6\]                        \[(1,\,\,2,\,\,3,\,\,6)\]

\[7=1\times ~7\] etc.                  \[(1,\,\,7)\]

•                   Every non-zero number is a factor of 0.

Example: \[0=1,\,\,2,\,\,3,\,\,4...............\]

\[\left( \because \frac{0}{1}=0,\,\,\frac{0}{2}0,\,\,\frac{0}{1}=......... \right)\]

       Prime Factorization

•                   When a number is expressed as the product of prime numbers, it is called the Prime factorization of the given number.

Examples:

\[\therefore 45=3\times 5\times 5\]

\[\therefore 144=2\times 2\times 2\times 2\times 3\times 3\]

       Highest Common Factor (H.C.F.)

•                   HCF of two or more numbers is the greatest number that divides each of them exactly.

To find the HCF of given number proceed as follows:

•                   Break the given number into prime factor.
•                   Find their common factors and multiply them.

Examples: H.C.F. of 15 and 35

\[15=3\times 5\]

\[35=5\times 7\]

Common factor of 15 and 35 is 5.

Hence HCF of 15 and \[35=5\]

       H.C.F. by common Davison method

•                  Divide the greater number by the smaller number, divide the divisor by the remainder, and divide the remainder by the next remainder, and so on until no remainder is left. The last divisor is the required HCF.

Example: HCF of 14 and 35 by method of Division

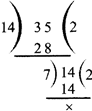
Thus HCF of 14 and 35 in 7.

         H.C.F. of more than two numbers

•                   First of all find the HCF of any two of the given numbers and then find the HCF of this HCF and third number and so on. The last divisor will be the required HCF.

Example: HCF of 6, 28 and 44

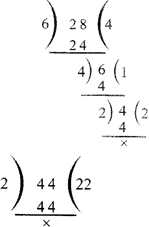
So, the require HCF is 2

Multiple: A multiple of a number is a obtained by multiplying it by a natural number.

Examples: Multiplies of 36 are \[36\times 1=36,\,\,36\]\[\times 2=72,\,\,36\times 3=144\ldots .\] And so on

        Properties of Multiples  

•                   Every number is a multiple of 1

Example:

\[3=1\times 3\]   \[4=1\times 4\]

\[15=1\times 15\]           \[17=1\times 17\]

•                   Every non-zero multiple of a non-zero number is greater than or equal to the number

Example: Multiple of 3 are 3, 6, 9, 12, each of them is greater than equal to 3.

•                  Infinite number of multiples of a non-zero numbers.
•                   0 is a multiple of every number.

       Least common multiple

•                  The LCM of two of more given numbers is the least number which is exactly divisible by each of them.

To find the LCM of two or more numbers

•                   Resolve the given number into prime factors and then find the product of the highest power of all the factors that appear in the given numbers. The product will be the LCM.

Example: LCM of 6, 14, 7, 32

\[6=2\times 3\]

\[14=2\times 7\]

\[7=1\times 7\]

\[32=2\times 2\times 2\times 2\times 2\]

Prime factors of the given numbers are 2, 3, 7 and their highest powers are\[{{2}^{5}},\,\,3\] and \[7\]

Hence, LCM \[=2\times 5\times 3\times 7=672\]

       LCM by short division method

•                    Write down the given numbers on a line separating them by commas.
•                    Divide by a number which divides at least two of them
•                    Set down the quotient and that undivided number in a line below the first.
•                    Repeat this process until you get two of the numbers which are divisible by the same number. The producer of the divisor and all last line will be the required LCM.
•                    LCM of 16, 24, 36 and 64

\[\therefore \,\,LCM=2\times 2\times 2\times 3\times 3\times 2\times 3=432\]