5th Class Mathematics Decimals

Decimals

• Decimal numbers: Fractions with 10, 100, 1000 or any multiple of 10 are called decimal numbers.

• Decimal numbers have two parts:

(a) Whole number (Part which is on the left hand side to the decimal point)

(b) Decimal part (Part which is on the right hand side to the decimal point)

e.g., In the decimal number 5.789, 5 is the whole number part and 789 is decimal part read as five point seven eight nine.

• Place value Chart of decimal numbers:

As we move from right to left, the value of digits increases by 10 times.

As we move from left to right, its value decreases by 10 times.

• Expanded form of decimals:

To express a number in expanded form, write each digit of the number with its corresponding place value with a + sign between them.

e.g., 45.459 = 4 tens + 5 ones + 4 tenths + 5 hundredths + 9 thousandths          

                  \[=40+5+\frac{4}{10}+\frac{5}{100}+\frac{9}{1000}\]

Adding any number of zeroes to the right of a significant digit in the decimal part does not change its value.

e.g., 3.4 is the same as 3.40 or 3.400 etc., whereas 3.04 is not the same as 3.004 etc.

The places of the digits are to be taken into consideration.

• Converting Decimals into Fractions:

(i) To convert a decimal number into a fraction, write the decimal number without the decimal point as the numerator of the fraction.

(ii) Write the denominator of the fraction by inserting as many zeroes on the right of 1 as the number of decimal places in the given decimal number.

(iii) Simplify the fraction if possible, i.e., write the fraction in the lowest terms. e.g. 78.59 = \[\frac{7859}{100}\]

• Like and unlike decimals: The decimal numbers having the same number of decimal places (digits after the decimal point) are called Like Decimals.

e.g., 20.89, 4.02, 45.94 and 0.23 are called like decimals.

The decimal numbers having different number of decimal places (digits after the decimal point) are called Unlike Decimals.

Unlike decimals may or may not be equivalent decimals.

e.g., 12.455, 1.23, 78.5 and 42.555 are unlike decimals.

• Equivalent Decimals: The decimals obtained by multiplying and dividing a given decimal number by multiples of 10 are called equivalent decimals.

e.g., 0.7, 0.70, 0.700 etc.

• Converting unlike decimals into like decimals:

To convert unlike decimals to like decimals, find the number in which the largest number of decimal places is present, and change the other decimals into their equivalent decimals, with the same number of decimal places as the largest number of decimal places.

e.g., 50.36, 459.2656

459.2656 has four decimal places.

50.36 has two decimal places.

50.3600 is an equivalent decimal for 50.36.

Hence, 50.3600, 459.2656 are like decimals.

• Comparing two decimal numbers:

We can compare two like decimals just as we compare two whole numbers ignoring the decimal point.

For comparing two unlike decimals, first convert them into like decimals and then compare.

• Addition of Decimals:

(i) Addition of decimals is similar to addition without decimal, in which we place the addends in such a way that the decimal point of all the numbers are in the same column.

(ii) Add the numbers ignoring the decimal point.

(iii) Place the decimal point in the sum directly under the decimal point of all the addends.

(iv) If numbers are unlike decimals convert them into like decimals and then add.

e.g., What is the sum of 450.36, 45.56 and 12.369?

Solution:       

• Subtraction of Decimals:

(i) Place the larger number first and the smaller number below it in such a way that the decimal point of both the numbers are in the same column.

(ii) Subtract the number (ignoring the decimal point) as in the case of whole numbers.

(iii) Place the decimal point in the result directly under the decimal point of the two given decimals.

e.g., Subtract 22.89 from 78.56.

• Multiplication of decimals:

(a) Multiplication of a decimal number by a whole number

e.g., Find the product of 45.98 and 8.

Step 1: Multiply the given numbers as whole numbers ignoring the decimal point.

Step 2: In the product, place the decimal point after so many digits from the right as the number of decimal places in the multiplicand.                      

In 45.98, the number of decimal places is 2. So, in the product 36784, place the decimal point after 2 places from the right.

Thus, \[45.98 \times  8 = 367.84\]

(b) Multiplication of a decimal number by a decimal number

e.g., Find the product of 45.98 and 8.5.

Step 1: Multiply the given numbers as whole numbers ignoring the decimal point.

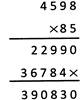
Step 2: In the product, place the decimal point after so many digits from the right as the sum of number of decimal places in the multiplicand and the multiplier.

Total number of decimal places in the multiplicand and the multiplier is 2 + 1 =3.

So, in the product 390830, place the decimal point after 3 digits from the right.

Thus, 45.98 x 8.5 = 390.830 = 390.83

(The last 0 can be ignored as it does not alter the value of the decimal.)

• Division of decimal numbers:

(a) Division of a decimal number by a whole number

Divide the decimal number by the whole number as usual division of whole numbers.

After the whole number part is divided, place a decimal point in the quotient before dividing the decimal part. Continue the division till the remainder is zero or up to a desired number of decimal places.

If the whole number part of the decimal number is 0, first place a 0 and a decimal point beside it in the quotient. Divide as usual until zero is obtained as remainder or up to a desired number of decimal places.

Shortcut to multiply a decimal number by multiples of 10:                            

Note: When a decimal number is multiplied by multiples of 10, the decimal point shifts right by the number of places as the number of zeroes in the multiple of 10.

Shortcut to divide a decimal number by multiples of 10:

• Rounding off and Estimation:

To round off a decimal number to 2 decimal places, we consider the digit in the third I place, (thousandths place). If it is < 5, we round the number down. If it is >= 5. We round the number up.                                                

e.g., Round off 43.256 to 2 decimal places.

In 43.256, the thousandths digit 6 > 5. So, we round it up as 43.26 to 2 decimal places.

The same procedure is carried out for rounding off to 1 decimal place.

e.g., 52.14 is 52.1 when rounded to 1 decimal place, as 4 < 5.

To round off a decimal number to the nearest whole number, we consider the tenths place and round it up or down as usual.

To check whether the answers are reasonable, we estimate by rounding off the decimal to the nearest whole number.

e.g., \[3.42 \times  15~\,\,=3\,\times  15=45\]