Fractions and Decimals
Category : 4th Class
Fractions and Decimals
Fraction
Fraction is used to indicate a part of a whole. Fraction is written, for example, as\[\frac{a}{b}\]. The top number in a fraction is called numerator and the bottom number is called denominator of the fraction. Hence in the given example 'a' is numerator and 'b' is denominator.
Look at the shaded part in the following figures which has been represented by fractions:
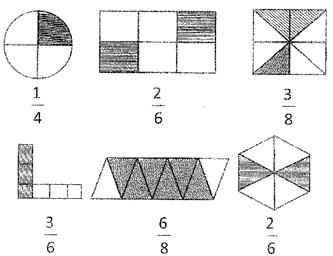
Tom cuts an apple into 5 equal parts. He eats one part. Give the part of the apple eaten by Tom in fraction.
Solution:
Tom eats 1 out of 5 parts.
So parts of apple eaten by Tom \[=\frac{1}{5}\]
Like Fraction
The fractions having same denominator are called like fractions.
For example, \[\frac{1}{5},\frac{4}{5},\frac{7}{5}\] are like tractions.
Choose the like fractions from the following?
\[\frac{45}{41},\frac{25}{13},\frac{13}{25},\frac{57}{61},\frac{6565}{13}\]
Solution:
\[\frac{25}{13}\]and \[\frac{6565}{13}\]are like fractions because they have same denominator.
Unlike Fraction
The fractions having different denominators are called unlike fractions.
For example, \[\frac{1}{2},\frac{6}{8},\frac{14}{17},\frac{13}{9}\]are unlike fractions.
Which of the following are unlike fractions?
\[\frac{4}{7},\frac{3}{5},\frac{8}{9},\frac{7}{5},\frac{11}{12},\frac{13}{17}\]
Solution:
\[\frac{4}{7},\frac{8}{9},\frac{11}{12},\frac{13}{17}\]are unlike fractions because they have different denominators.
Conversion of Unlike Fraction into Like Fraction
Multiply the numerator and denominator of each fraction by a suitable number (one number for one fraction) such that denominator becomes same in all fraction.
Convert \[\frac{5}{7}\] and, \[\frac{7}{8}\] into like fractions.
Solution:
\[\frac{5\times 8}{7\times 8}=\frac{40}{56}\]
And, \[\frac{7\times 7}{8\times 7}=\frac{49}{56}\]
\[\frac{40}{56}\] and \[\frac{49}{56}\] are like fractions.
Equivalent Fraction
The fractions which have same value are called equivalent fractions.
For example, \[\frac{7}{9}\]and \[\frac{28}{36}\]are equivalent fractions.
Finding an Equivalent Fraction of Given Fraction
To find an equivalent fraction of a given fraction, numerator and denominator of the fraction is multiplied or divided by same number.
Find an equivalent fraction of \[\frac{15}{17}\].
Solution:
Equivalent fraction of\[\frac{15}{17}=\frac{45}{51}\]
Note: You may find other equivalent fraction of \[\frac{15}{17}\]
Unit Fraction
The fractions in the form \[\frac{p}{q}(p=1,q\] is a natural number) are called unit fractions.
For example, \[\frac{1}{4},\frac{1}{5},\frac{1}{6}\] are unit fractions.
Proper Fraction
The fractions having greater denominator are called proper fractions.
For example, \[\frac{21}{25}\] is a proper fraction because in this fraction numerator is smaller than denominator.
Improper Fraction
The fractions having smaller denominator are called improper fractions.
For example, \[\frac{21}{17}\] is an improper fraction because in this fraction numerator is greater than denominator
Mixed Fraction
Mixed fraction is a sum of a whole number and a proper fraction.
For example, \[1\frac{4}{17}\] is a mixed fraction, because 1 is a whole number and \[\frac{4}{17}\] is a proper fraction.
Conversion of Mixed Fraction into Improper Fraction
If \[a\frac{b}{c}\] is a mixed fraction/ then \[\frac{(a\times c)+b}{c}\] is an improper fraction equivalent to given mixed fraction.
Convert \[\mathbf{12}\frac{3}{11}\] into the improper fraction.
Solution:
\[\mathbf{12}\frac{3}{11}=\frac{11\times 12+3}{11}=\frac{132+3}{11}=\frac{135}{11}\]
Point to note
· \[\frac{p}{q}\]is a proper fraction, if\[p<q\]
· \[\frac{p}{q}\]is an improper fraction, if \[p>q\]
· \[p\frac{q}{r}\]is a mixed fraction where p is whole number and\[\frac{q}{r}\] is a proper fraction
Addition of Like Fractions
Like fractions are the fractions with same denominator. So, for the addition of like fractions simply add the numerators and write the sum over the common denominator.
Add the following fractions.
\[\frac{5}{7},\frac{1}{7},\frac{6}{7}\]
Solution:
\[\frac{5}{7}+\frac{1}{7}+\frac{6}{7}=\frac{12}{7}\]
Subtraction of Like Fractions
In subtraction, like addition, simply subtract the numerators and write the sum over the common denominator.
Subtract \[\frac{7}{16}\]from \[\frac{9}{16}\]
Solution
\[\frac{9}{16}-\frac{7}{16}=\frac{2}{16}\]
Decimals
A decimal number is broadly divided into two parts.
(i) Whole number part
(ii) Decimal part
The two parts are separated by a dot (.) called the decimal point.
From the decimal point as you move on the left the place value is multiplied by 10 and as you move on the right it is divided by 10.
|
Decimal fraction |
Whole part |
Decimal part |
|
5.3 |
5 |
3 |
|
147.81 |
147 |
.81 |
|
15.679 |
15 |
.679 |
|
.8 |
0 |
.8 |
|
1.004 |
1 |
.004 |
Look at the following table:
|
Thousand |
Hundreds |
Tens |
Ones |
|
4 |
4 |
4 |
4 |
The number given in the place value chart can be written \[4000+400+40+4.\] We notice/ as we move right in the place value chart, the value of the place gets one-tenths of the previous one.
So far we have studied the place value chart having unit place in extreme right side.
Now we will know about the decimal place value chart, which goes right to the unit place.
Decimal Place Value Chart
|
Thousand |
Hundred |
Tens |
Ones |
Tenth |
Hundredths |
Thousandths |
Ten thousandths |
|
1000 |
100 |
10 |
1 |
1/10 |
1/100 |
1/1000 |
1/10000 |
Expanded form of Decimals
The expanded form of a decimal number is the number written as the sum of its whole number and decimal place values.
Write the decimal 54.321 into expanded form.
Solution
\[50+4+\frac{3}{10}+\frac{2}{100}+\frac{1}{1000}\]
Write the required decimal for \[\mathbf{300+4+}\frac{\mathbf{0}}{\mathbf{10}}\mathbf{+}\frac{\mathbf{5}}{\mathbf{100}}\mathbf{+}\frac{\mathbf{7}}{\mathbf{1000}}\]
Solution:
304.057
Like Decimals
The decimals having equal number of decimal places are called like decimals.
\[4\mathbf{5}.\mathbf{326},\mathbf{3698}.\mathbf{222},\mathbf{0}.\mathbf{003}\]are like decimals because they have equal number of decimal places.
Unlike decimals
The decimals having unequal number of decimal place are called unlike decimals.
78.036, 98,000032 are unlike decimals, because they have unequal number of decimal places.
Equivalent Decimals
The decimals having same value are called equivalent decimals.
78.325 and 78.3250 are equivalent decimals, because they have same value
Comparison of decimals
If there are two decimal numbers we can compare them, that is, whether a number is greater than less than, or equal to other number?
A decimal is just a fractional number. For .ample, compare 0.9 and 0.09 becomes clear if we compare\[\frac{9}{10}\] to \[\frac{9}{100}\]. The fraction\[\frac{9}{10}\], is equivalent to \[\frac{9}{100}\] which is clearly greater than \[\frac{9}{100}\].
Therefore, when decimals are compared, start with tenth place and then go on. If one decimal has a higher number in teeth place, it is large then the decimal with fewer tenth. If tenth are equal, compare the hundreds, then thousands etc., until one decimal is larger, or there are no more place to compare.
Find the greater decimal.
5465.252, 3465.655
Solution:
5465252 > 3465.655
Which one is greater
5447.87901, 5447.87910
Solution:
\[5447.87901<5447.87910\]
Addition of Decimals
Put whole part under whole part and decimal part under decimal part. Then do simple addition.
Add: \[\mathbf{5411}.\mathbf{322}+\mathbf{8254}.\mathbf{5461}+\mathbf{0}.\mathbf{5422}\]
Solution:
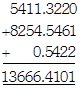
\[\mathbf{545}.\mathbf{23}+\mathbf{54232}.\mathbf{544}+\mathbf{0}.\mathbf{00001}+\mathbf{8755}.\mathbf{2}\]
Solution:
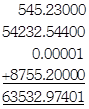
Subtraction of Decimals
Put whole part under whole part and decimal part under decimal part and do simple subtraction.
\[\mathbf{5446}.\mathbf{20}-\mathbf{455}.\mathbf{0005}\]
Solution:
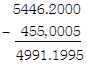
\[\mathbf{74}.\mathbf{154}-\mathbf{54}.\mathbf{23}\]
Solution:
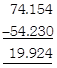
Multiplication of Decimals by Power of 10
Shift the decimal point to right as many places as there are zeroes in the power of 10.
Multiply: \[\mathbf{394}.\mathbf{5607}\times \mathbf{1000}\]
Solution:
\[394.5607\times 1000=394560.7\]
\[\mathbf{A}=\mathbf{2465}.\mathbf{21},\text{ }\mathbf{B}=\mathbf{100}\]. Find the value of \[\mathbf{A}\times \mathbf{B}.\]
Solution:
\[2465.21\times 100=246521\]
Multiplication of a Decimal and a Whole Number
Multiply the decimals like normal multiplication and put the decimal point such that the product have same number of decimal places as in the multiplicand.
Find the product of 6556.65 and 5.
Solution:
\[6556.65\times 5=32783.25\]
Division of a Decimal by the Power of 10
Shift the decimal point, starting from right towards left to the number of places, equal to number of zeroes in denominator
Divide 54462. 21 by 1000
Solution:
\[54462.21\div 1000=54.46221\]
You need to login to perform this action.
You will be redirected in
3 sec
