Division of a Decimal by the Power of 10
Category : 4th Class
Division of a Decimal by the Power of 10
Case 1: When a decimal is divided by 10. Like \[\text{5456}.\text{32}\div \text{1}0\] The decimal is shifted one digit left. Thus \[\text{5456}.\text{32}\div \text{1}0=\text{545}.\text{632}\]
Case 2: When a decimal is divided by 100. Like \[\text{5456}.\text{32}\div \text{1}00\] The decimal is shifted two digit left. Thus\[\text{5456}.\text{32}\div \text{1}00=\text{54}.\text{5632}\]
Case 3: When a decimal is divided by 1000. Like\[~\text{5456}.\text{32}\div \text{1}000\] The decimal is shifted three digit left. Thus \[\text{5456}.\text{32}\div \text{1}000=\text{5}.\text{45632}\]
Note: As you increase the power of 10 by one, the decimal point shift one digit left.
For example: \[5463.23\div {{10}^{1}}=546.323\] \[5463.23\div {{10}^{2}}=54.6323\] \[5463.23\div {{10}^{3}}=5.46323\]
Divide 786.45 by 100
Solution:
100 contains two zeroes, therefore, shift the point two digit left in the decimal. Thus\[\text{786}.\text{45}\div \text{1}00=\text{7}.\text{8645}\]
Represent the shaded part of the following figures as fraction and choose what kind of fractions they are?
Figure (i) Figure (ii)
(a) They are like fractions.
(b) They are unlike fractions.
(c) They are equivalent fractions.
(d) All of these
(e) None of these
Answer (a)
Explanations-
In the figure (i), 4 parts out of 8 parts are shaded. Thus fractional representation for the shaded part\[=\frac{4}{8}\] In the figure (ii), 6 parts out of 8 parts are shaded. Thus fractional representation for the shaded part\[=\frac{6}{8}\] Both the representations have same denominator. Therefore, they are like fractions.
Which one of the following is the equivalent fraction of\[\frac{7}{8}\]?
(a) \[\frac{9}{8}\]
(b) \[\frac{7}{9}\]
(c) \[\frac{35}{40}\]
(d) \[\frac{11}{40}\]
(e) None of these
Answer (c)
Explanation-
When we multiply both numerator and denominator of the fractionby 5, we get\[\frac{35}{40}\]. Thus,\[\frac{35}{40}\]and\[\frac{7}{8}\]are equivalent fractions.
Jack: \[\frac{7}{9}\]and\[\frac{7}{13}\], are like fractions as both has same numerator.
Cody: To be like fractions, denominators of the fractions should be same instead of numerator. Who is correct?
(a) Jack
(b) Cody
(c) Both of them are correct
(d) Both of them are partially incorrect
(e) None of these
Answer (c)
Represent the yellow part in the following figure as fraction and find its one equivalent fraction.
| Red | Yellow | Green | Yellow | Red |
(a) \[\frac{22}{60}\]
(b) \[\frac{4}{20}\]
(c) \[\frac{6}{20}\]
(d) \[\frac{32}{60}\]
(e) None of these
Answer (b)
In which one of the following figures shaded part represents\[\frac{1}{5}\]?
(a) 
(b)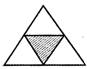 
(c) 
(d)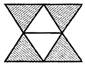 
(e) None of these
Answer (c)
Which one of the following is not a proper fraction?
(a) \[\frac{1}{5}\]
(b) \[\frac{2}{5}\]
(c) \[\frac{3}{5}\]
(d) \[\frac{7}{5}\]
(e) None of these
Answer (d)
Explanation-
Numerator is greater than denominator in the fraction\[\frac{7}{5}\].Thus\[\frac{7}{5}\]is an improper fraction.
\[\frac{p}{q}\]is a fraction. If p is greater than q, which one of the following is correct?
(a) \[\frac{p}{q}\]is a proper fraction
(b) \[\frac{p}{q}\]is an improper fraction
(c) \[\frac{p}{q}\]is a unit fraction
(d) All of these
(e) None of these
Answer (b)
Explanations- p is greater than q, therefore,\[\frac{p}{q}\]is an improper fraction.
How many parts of the following figure would you like to shade such that shaded part of the figure can represents unit fraction?
(a) One part
(b) Two parts
(c) Three parts
(d) Four parts
(e) None of these
Answers (a)
Convert the given mixed fraction into improper fraction\[7\frac{7}{12}\].
(a) \[\frac{12}{91}\]
(b) \[\frac{91}{12}\]
(c) \[\frac{7}{12}\]
(d) \[\frac{27}{91}\]
(e) None of these
Answer (b)
Jack: \[\frac{19}{11}\]is an improper fraction.
Cody: \[\frac{19}{11}\]can be changed into mixed fraction. Who is correct?
(a) Jack is correct
(b) Cody is correct
(c) Both of them are correct
(d) Both of them are partially incorrect
(e) None of these
Answer (c)
Find the fraction that should be added to\[\frac{8}{9}\]to get\[\frac{31}{18}\]?
(a) \[\frac{5}{6}\]
(b) \[\frac{23}{18}\]
(c) \[\frac{7}{9}\]
(d) \[\frac{8}{9}\]
(e) None of these
Answer (a)
Explanations-
Let the fraction X should be added to\[\frac{8}{9}\] According to the question\[\frac{8}{9}\times X=\frac{31}{18},X=\frac{31}{18}-\frac{8}{9},X=\frac{5}{6}\]
Zacob has 8 liters of milk. He uses\[2\frac{1}{2}\]liters for pudding and\[2\frac{1}{8}\]liters for curd. What quantity of milk is left with him?
(a) \[\frac{21}{26}\]
(b)\[\frac{5}{27}\]
(c) \[\frac{8}{27}\]
(d) \[\frac{27}{8}\]
(e) None of these
Answer (d)
Explanations-
Total milk Zacob has = 8 L Total milk used by Jacob \[=2\frac{1}{2}L+2\frac{1}{8}L\] Or\[(\frac{5}{2}+\frac{17}{8})L=(\frac{20+17}{8})L=\frac{37}{8}L,\], So remaining milk\[=8-\frac{37}{8}=\frac{27}{8}L\]
Arrange the following in ascending order:
\[\frac{2}{3},\frac{4}{9},\frac{5}{7},\frac{5}{3}\]
(a) \[\frac{4}{9},\frac{2}{3},\frac{5}{7},\frac{5}{3}\]
(b) \[\frac{2}{3},\frac{4}{9},\frac{5}{3},\frac{5}{7}\]
(c) \[\frac{2}{3},\frac{5}{3},\frac{4}{9},\frac{5}{7}\]
(d)\[\frac{2}{3},\frac{4}{9},\frac{5}{7},\frac{5}{3}\]
(e) None of these
Answer (a)
Find the perimeter of the following figure.
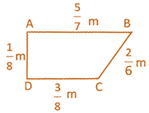
(a) \[\frac{198}{168}m\]
(b) \[\frac{230}{168}m\]
(c) \[\frac{250}{168}m\]
(d) \[\frac{65}{42}m\]
(e) None of these
Answer (d)
What is the difference of the fractions if shaded part in the following figures are represented as fraction?
Figure (i) Figure (ii)
(a) \[\frac{7}{10}\]
(b) \[\frac{7}{30}\]
(c) \[\frac{11}{30}\]
(d)\[\frac{14}{30}\]
(e) None of these
Answers (c)
Which one of the following is true for 0.003
(a) Three-tenth
(b) Three-hundredth
(c) Three-thousandth
(d) Three-ten thousandth
(e) None of these
Answer (c)
Explanation-
\[0.003=\frac{3}{1000}\] (three-thousandth)
John makes a rectangular figure and divides it into 100 equal parts. He shades 3 parts out of every 10 parts. Find the correct expression for the shaded part.
(a) \[\frac{1}{100}\]
(b) \[\frac{10}{100}\]
(c) \[\frac{3}{100}\]
(d) \[\frac{30}{100}\]
(e) None of these
Answer (d)
Explanation-
John shades 3 parts out of every 10 parts and there are 100 parts in the figure. So he shades 30 parts. Therefore, correct expression for the figure ls\[\frac{30}{100}\].
Which one of the following is the correct decimal representation for the shaded part in the figure?
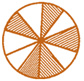
(a) 0.1
(b) 0.2
(c) 0.5
(d) 0.4
(e) None of these
Answer (c)
Which one of the following is correct decimal expression for the place value of 5?
| Ones | Decimal Point | Tenths | Hundredths |
| 3 | . | 0 | 5 |
(a) 0.5
(b) 0.05
(c) 0.005
(d) 0.0005
(e) None of these
Answer (b)
You have to arrange the digits of the decimal 35.564 in the decimal place value chart. Which one of the following places is suitable for the digit 4?
(a) Ones
(b) Tens
(c) Hundredths
(d) Thousandths
(e) None of these
Answer (d)
Choose the correct option for 50.203.
(a)\[50+20+\frac{3}{10}\]
(b) \[50+\frac{2}{10}+\frac{3}{100}\]
(c) \[50+\frac{2}{10}+\frac{3}{1000}\]
(d) \[5+\frac{2}{10}+\frac{3}{100}\]
(e) None of these
Answer (c)
Explications-
In the decimal 50.203, 5 is at the tens place, 2 is at the tenths place, and 3 is at the hundredths place. Thus, expanded form of 50.203 is\[50+\frac{2}{10}+\frac{3}{1000}\].
Which one of the following is the equivalent decimal of 623.523?
(a) 623.52300
(b) 623.5023
(c) 62.3523
(d) 0.623523
(e) None of these
Answers (a)
Expirations-
If we add zero extreme right to the decimal, the value of the decimal does not get changed. But if we change the place of decimal, the value of the decimal get changed. Therefore, 623.52300 is a equivalent decimal of 623.523.
215.0A2 and 215.0B3 are two decimals. Which one of the following is not true?
(a) If A = B, 215.0A2 < 215.0B3
(b) If A >B, 215.0A2 > 215.0B3
(c) If A <B, 215.0A2 < 215.0B3
(d) If A = B, 215.0A2 and 215.0B3 are equivalent decimals.
(e) None of these
Answer (d)
P is the extreme right digit of a decimal. If place value of P is\[\frac{p}{1000}\], how many decimal places the decimal has?
(a) One
(b) Two
(c) Three
(d) Four
(e) None of these
Answers (c)
Jack: When we multiply a decimal by 10 we get an equivalent decimal of that decimal.
John: When we multiply a decimal by 10 its value is changed. Equivalent decimals have same value therefore; we cannot find an equivalent decimal by multiplying the decimal by 10. Who is correct?
(a) Jack
(b) John
(c) Both are correct
(d) Both are partially incorrect
(e) None of these
Answers (b)
Add: 131.298 + 16.042 + 2.468 + 8.234
(a) 159.33
(b) 158.033
(c) 258.33
(d) 151.33
(e) None of these
Answers (b)
Explanations-
\[\begin{align} & \text{131}.\text{289} \\ & \,\,\,\text{16}.0\text{42} \\ & \,\,\,\,\,\,\text{2}.\text{468} \\ & +\,\,\,\text{8}.\text{234} \\ & \overline{\underline{\text{158}.0\text{33}}} \\ \end{align}\]
Find the value of A. If A = 331.000 ? 96.042
(a) 344.345
(b) 453.786
(c) 234.958
(d) 234.876
(e) None of these
Answer (c)
Explanation
\[\begin{align} & \,\,\,\text{331}.000 \\ & -\text{ 96}.0\text{42} \\ & \,\,\,\overline{\underline{\text{234}.\text{958}}} \\ \end{align}\]
\[''0.02002\times {{10}^{4}}=200.2''\]In the given expression 0.02002 is multiplied by 104 and the product is 200.2. Jack replaces\[{{10}^{4}}\]P thus he finds the product gets changed and it becomes 2.002. Find the value of P
(a) \[{{10}^{1}}\]
(b) \[{{10}^{2}}\]
(c)\[{{10}^{5}}\]
(d)\[{{10}^{3}}\]
(e) None of these
Answer (b)
By what number 4562.2 should be divided to obtain the decimal 4.5622?
(a) 10
(b) 100
(c) 1000
(d) 10000
(e) None of these
Answer (c)
Which one of the following is true for\[0.\text{45}\times \]\[\text{1}00\times \text{56}\]?
(a) 2205
(b) 1825
(c) 2025
(d) 2520
(e) None of these
Answer (d)
You need to login to perform this action.
You will be redirected in
3 sec
