2nd Class Mathematics Division Division

LEARNING OBJECTIVES

This lesson will help you to:—

• know about division
• learn the method of division.
• write a division problem.
• solve a division problem.

QUICK CONCEPT REVIEW

DIVISION

Division means equal sharing or making groups of equal things.

Let us understand with the help of an example.

Maria has 4 rabbits. She has 8 carrots that she wants to distribute equally among them. How many carrots will each rabbit get?

This can be solved by using Division

First Maria will give one carrot to each rabbit

Step 1

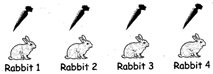
Then she finds that she still has some carrots. Now she gives one more carrot to each rabbit.  

Step 2

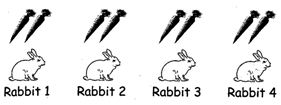
There is no more carrot left now. Each rabbit gets 2 carrots. 

So, here Maria equally divides 8 carrots among 4 rabbits.  

Real Life Examples

• When you are eating a pizza, you have to divide the pizza in equal parts so that everyone gets an equal share, you can use division.
• If you have 10 chocolates and you want to share it with you want to share it with your 5 friend then you can use the method of division.

Properties of Division

1. It is the reverse of multiplication.
2. Division is repeated subtraction.
3. '-' is the symbol of division.
4. It does not always happen that a number divides completely. Sometimes some number is left that cannot be divided any further. Such a number is called remainder.

5. Dividing a number by 1

When we divide a number other than 0 by 1, we get the number itself.

For example       \[\text{8}\div \text{1}=\text{8}\]

                                \[\text{1}0\text{ }\div \text{ 1 }=\text{ 1}0\]

6. Dividing O by a number

When we divide zero by a number we get '0' as answer.

For example:     \[0\div 6=0\]

                                \[0\div 13=0\]

7. Dividing a number by itself

When we divide a number other than zero by the number itself we get 1 as answer.

For example:     \[10\div 10=1\]

                                \[13\div 13=1\]

                                \[0\div 0=0\]

Historical Preview

• An obelus \[(\div )\]is a symbol consisting of a short horizontal line with a dot above and below. The word ‘obelus’ comes from ancient Greek word for a sharpened stick or pointed pillar.

Methods of Division

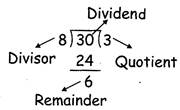
1. Short division with remainder method:

Divide 30 by 8.

It can also be written as \[30\div 8\]

Step 1: Arrange the numbers in the following manner \[8\overline{\left){30}\right.}\]

Step 2: We divide from left

\[\text{8 }\times \text{ 3 }=\text{ 24}\]which is less than 30

\[\text{8 }\times \text{ 4 }=\text{ 32}\]which is more than 30

we take 3 as quotient

\[\text{8 }\times \text{ 3 }=\text{ 24}\]

\[\text{3}0\text{ }-\text{ 24 }=\text{ 6}\]

Thus we have

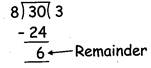
2. Division with no remainder:

Let us consider an example where no remainder is left on division.

Divide93 by 3 or \[93\div 3\]

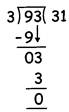
Now, consider division of 930 by 3.

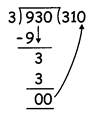
Here the zero left in the dividend will shift to the quotient.

3. Long Division Method:

Divide 93 by 4 using long division method

Step 1: Arrange the numbers in the following manner.             

\[4\overline{\left){93}\right.}\]

Step 2: We divide from left.

\[\text{4}\times \text{2}=\text{8}\]which is less than 9 and

\[\text{4}\times \text{3}=\text{12}\]greater than 9

We take 2 as quotient

\[\text{4}\times \text{2}=\text{8}\]

\[\text{9}-\text{8}=\text{1}\]

Step 3: We see\[\text{4}\times \text{3}=\text{12}\]which is less than 13 and\[\text{4 }\times \text{ 4 }=\text{ 16}\]which is more than 13.

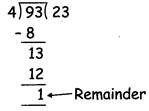
Basic term used in division

1. Dividend: It is the number that we divide
2. Divisor: It is the number with which we divide.
3. Quotient: It is the result obtained on division
4. Remainder: It is the number left undivided

Relation between Dividend, Divisor. Quotient and Remainder:

\[\text{Dividend }=\text{ }\left( \text{Quotient }\times \text{ Divisor} \right)\text{ }+\text{ Remainder}\]

Do you know?

• Division is always done from the left side unlike addition, subtraction and multiplication.