JEE Main & Advanced Physics Wave Mechanics Equation of a Plane Progressive Waves

(1) If during the propagation of a progressive wave, the particles of the medium perform SHM about their mean position, then the waves is known as a harmonic progressive wave.

(2) Suppose a plane simple harmonic wave travels from the origin along the positive direction of x-axis from left to right as shown in the figure.

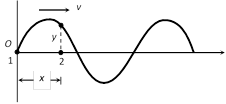
The displacement y of a particle 1 at O from its mean position at any time t is given by \[y=a\sin \omega \,t.\]

The wave reaches the particle 2 after time \[t=\frac{x}{v}\]. Hence displacement y of a particle 2 is given by

\[y=a\sin \omega \,\left( t-\frac{x}{v} \right)\]\[=a\sin (\omega \,t-kx)\]                              \[\left( \because \,k=\frac{\omega }{v} \right)\]  

The general equation of a plane progressive wave with initial phase is

(3) Various forms of progressive wave function.

(i) \[y=a\,\sin \,(\theta t-kx)\]

(ii) \[y=a\,\sin \,(\omega t-\frac{2\pi }{\lambda }x)\]

(iii) \[y=a\sin 2\pi \left[ \frac{t}{T}-\frac{x}{\lambda } \right]\]

(iv) \[y=a\sin \frac{2\pi }{T}\left( t-x\frac{T}{\lambda } \right)\]

(v) \[y=a\sin \frac{2\pi }{\lambda }(vt-x)\]

(vi) y = \[a\sin \omega \,\left( t-\frac{x}{v} \right)\]

(4) Particle velocity : The rate of change of displacement y w.r.t. time t is known as particle velocity

Hence from \[y=a\sin \,(\omega \,t-kx)\]

Particle velocity \[{{v}_{p}}=\frac{\partial y}{\partial t}=a\omega \,\cos (\omega \,t-kx)\]

Maximum particle velocity \[{{({{v}_{p}})}_{\max }}=a\omega \]

Also \[\frac{\partial y}{\partial t}=-\frac{\omega }{k}\times \frac{\partial y}{\partial x}\]\[\Rightarrow \]\[{{\upsilon }_{p}}=-v\times \] Slope of wave at that point

(5) Important relations for numerical solving

(i) Angular frequency \[\omega =\] co-efficient of \[t\]

(ii) Propagation constant \[k=\] co-efficient of \[x\]  

Wave speed \[v=\frac{\text{co-efficient of }t}{\text{co-efficient of }x}=\frac{\omega }{k}\]

(iii) Wave length \[\lambda =\frac{\text{co-efficient of }x}{2\pi }\]

(iv) Time period \[T=\frac{2\pi }{\text{co-efficient of }t}\]

(v) Frequency \[n=\frac{\text{co-efficient of }t}{2\pi }\]

(vi) \[{{({{v}_{p}})}_{\max }}=a\omega =a(2\pi n)=\frac{a2\pi }{T}\]

(vii) If the sign between t and x terms is negative the wave is propagating along positive X-axis and if the sign is positive then the wave moves in negative X-axis direction.

(viii) Co-efficient of sin or cos functions i.e. Argument of sin or cos function is represented by phase i.e. \[(\omega t-kx)=\]Phase.

(ix) Phase difference and path difference : At any instant t, if \[{{\phi }_{1}}\] and \[{{\phi }_{2}}\] are the phases of two particles whose distances from the origin are \[{{x}_{1}}\] and \[{{x}_{2}}\] respectively then \[{{\varphi }_{1}}=(\omega \,t-k{{x}_{1}})\] and \[{{\varphi }_{2}}=(\omega \,t-k{{x}_{2}})\]\[\Rightarrow \]\[{{\varphi }_{1}}-{{\varphi }_{2}}=k({{x}_{2}}-{{x}_{1}})\]

\[\Rightarrow \]Phase difference \[(\Delta \varphi )=\frac{2\pi }{\lambda }\text{.}\,\text{Path difference (}\Delta x)\] \[(x)\]

(x)  Phase difference and time difference : If the phases of a particle distance \[x\] from the origin is \[{{\phi }_{1}}\] at time \[t\] and \[{{\phi }_{2}}\] at time \[{{t}_{2}},\] then \[{{\varphi }_{1}}=(\omega \,{{t}_{1}}-kx)\] and \[{{\varphi }_{1}}=(\omega {{t}_{2}}-kx)\]\[\Rightarrow \] \[{{\varphi }_{1}}-{{\varphi }_{2}}=\omega ({{t}_{1}}-{{t}_{2}})\]

\[\Rightarrow \]Phase difference \[(\Delta \varphi )=\frac{2\pi }{T}.\,\text{Time difference}\,\text{(}\Delta t)\]