Notes - Mathematics Olympiads - Trigonometry
Category : 11th Class
Trigonometry
Key Points to Remember
Trigonometry: It is derived/contained from two greek words trigon and metron means that the measurement of three sides of the triangle.
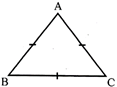
A triangle has three vertex, three angles and three sides in above figure.
vertex be A, Band C
Angle be \[\angle ABC,\] \[\angle BCA,\] and \[\angle CAB,\]or \[\angle BAC\]
According to sides, type of triangle be
(a) Equilateral Triangle: All sides are equal
(b) Isosceles Triangle: Two sides are equal
(c) Scalene Triangle: All sides are different.
According to Angle, There are three types of triangles:
(a) Acute Angle Triangle
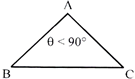
(b) Obtuse Angle Triangle
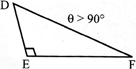
(c) Right angle Triangle
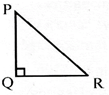
Sum of all angles in a triangle is \[180{}^\circ \]
In right angle triangle, basically, there are three triagonometrical ratio: sin, cosine and tangent.
i.e. total trigonometrical ratio are six:
sin, cos, tan, cosec, sec, cot
Let us consider a right angle triangle ABC in which
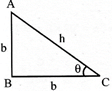
Then \[\angle A=90{}^\circ -\theta \]
\[\sin \theta =\frac{P}{h}=\frac{AB}{AC},\,\]\[\cos ec\,\theta =\frac{h}{P}\]
\[\cos \,\theta =\frac{b}{h},\] \[sec\theta =\frac{h}{b}\]
\[\tan \theta =\frac{P}{b},\] \[\cot \theta =\frac{b}{P}\]
Trigonometrical ratio shows the relation between angle and sides of the triangle.
|
\[\sin \theta \times \operatorname{cosec}\theta =1\] |
|
\[\tan \theta \times \cot \theta =1\] |
|
\[\cos \theta \times \sec \theta =1\] |
\[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\] …….. (1)
\[LHS={{\left( \frac{P}{h} \right)}^{2}}+{{\left( \frac{b}{h} \right)}^{2}}=\frac{{{P}^{2}}}{{{h}^{2}}}+\frac{{{b}^{2}}}{{{h}^{2}}}\]
|
\[{{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \] |
|
\[{{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \] |
\[=\frac{{{P}^{2}}+{{b}^{2}}}{{{h}^{2}}}=\frac{{{h}^{2}}}{{{h}^{2}}}=1\] [By pythagoras theorem]
Dividing equation (1) on both sides by \[{{\cos }^{2}}q,\]we have
\[\frac{{{\sin }^{2}}\theta }{{{\cos }^{2}}\theta }+\frac{{{\cos }^{2}}\theta }{{{\cos }^{2}}\theta }=\frac{1}{{{\sin }^{2}}\theta }\]
\[\Rightarrow {{\tan }^{2}}\theta +1={{\sec }^{2}}\theta \]
\[\Rightarrow {{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
\[{{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1\]
Again, dividing (1) by \[{{\sin }^{2}}\theta \], we have
\[\frac{{{\sin }^{2}}\theta }{{{\sin }^{2}}\theta }+\frac{{{\cos }^{2}}\theta }{{{\cos }^{2}}\theta }=\frac{1}{{{\sin }^{2}}\theta }\]
\[\Rightarrow 1+{{\cot }^{2}}\theta =\cos e{{c}^{2}}\theta \]
\[\Rightarrow \cos e{{c}^{2}}\theta -{{\cot }^{2}}\theta =1\]
\[{{\cot }^{2}}\theta =\cos e{{c}^{2}}\theta -1\]
Angle: Inclination between two sides (arms), is said to be an angle, e.g.
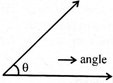
Angle may be positive or negative
When angle be measured in anticlockwise direction then it is positive otherwise negative.
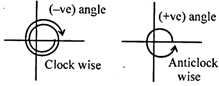
An angle is measured by three types.
In Sexagosimal system, Right angle = 90°
\[1{}^\circ \]= 60' (60 minutes) \[\because \,\,'\to \] minute 1' = 60" (In word sixty second)
In Centigecimal System, 1 right angle = \[{{100}^{g}}\]
(\[{{100}^{g}}\] is read as hundred grade)
\[{{1}^{g}}=100'\]
\[1'=100''\]
In radian/circular system, 180° = 2 right angle = \[{{\pi }^{c}}\]
(\[\because \,\,C\to \]Radian)
2 Right angle = \[{{\pi }^{c}}\]
Relation among Degree; grade and radian
\[{{100}^{g}}\]= 90°
\[2\times {{100}^{g}}=2\times 90{}^\circ ={{\pi }^{c}}\pi =\frac{22}{7}\]
\[\frac{G}{200}=\frac{D}{180{}^\circ }=\frac{c}{\pi }\]
\[\pi \]is an irrational number
1st of all, \[\pi \] is a greek word. It is ratio of circumference of the circle to its diameter.
i.e. \[\frac{\pi }{1}=\frac{Circumference}{Diameter\,of\,circle}\]
\[Circumference=\pi \times d\]
\[=\pi \times 2r\]
\[c=2\pi r,\]
Where, c = circumference, d = diameter of circle, r = radius of circle
\[\theta =\frac{\ell }{r}\]
\[\ell =\theta \times r\], where \[\theta \] is measured in radian, not in degree.
\[\ell \to \]arc of the circle
r = radius of the circle
\[\pi \] =180°
Purest value of \[\pi =\frac{355}{113}\] i.e. \[\left( \frac{22}{7}\,or\,3.1416 \right)\]
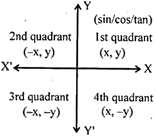
According to coordinate present of a point.
\[P\equiv (x,y),\] \[x\to \]abscissa
\[y\to \]ordinate
In 1st quadrent, all triagonometrical ratio (sin, cosine, tan /cot /cosec /sec) are positive.
In 2nd quadrant; sin/cosec are positive remaining trigonometrical ratio: i.e. (tan /cos /cot /sec) are negative.
In 3rd quadrant, tan/cot be positive and remaining are negative.
In 4th quadrant, cos/sec are positive and remaining T.R be negative.
|
Quadrant |
1st |
2nd |
3rd |
4th |
|
sin/cosec |
+ |
+ |
- |
- |
|
cos/sec |
+ |
- |
- |
+ |
|
tan/cot |
+ |
- |
+ |
- |
In allied angle, tips to remember the allied angle
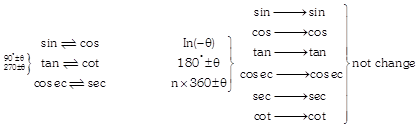
According to \[90{}^\circ \,\,\pm \,\,\theta,\] \[270{}^\circ \,\,\pm \,\,\theta ,\] \[180{}^\circ \,\,\pm \,\,\theta ,\]\[n\,\,\times 360{}^\circ \,\,\,\pm \,\,\,\theta ,\]\[(-\,\theta )\] we give the sign of allied angle in which quadrant these allied lie i.e. \[90{}^\circ -\theta \] lies 1st quadrant
In 1st quadrant, all T.R. are positive,
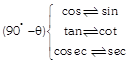
Hence, Result to be
\[\sin \,(90{}^\circ -\theta )=\cos \theta \]
\[cos\,(90{}^\circ -\theta )=\sin \theta \]
\[tan\,(90{}^\circ -\theta )=\cot \theta \]
\[cot\,(90{}^\circ -\theta )=\tan \theta \]
\[sec\,(90{}^\circ -\theta )=\cos ec\,\theta \]
Similarly,
\[90{}^\circ +\theta \to \] 2nd quadrant
Only, sin / cosec be positive and remaining are negative
\[sin(90{}^\circ +\theta )=+\cos \theta \]
\[cos(90{}^\circ +\theta )=-\sin \,\theta \]
\[tan\,(90{}^\circ +\theta )=-\cot \,\theta \]
\[cot\,(90{}^\circ +\theta )=-\tan \,\theta \]
\[\sec \,\,(90{}^\circ +\theta )=-\cos ec\,\theta \]
\[co\sec \,\,(90{}^\circ +\theta )=+sec\,\theta \]
\[180{}^\circ -\theta \to \] 2nd quadrant
\[\sin (180{}^\circ -\theta )=\sin \,\theta \]
\[cos\,(180{}^\circ -\theta )=-\cos \theta \]
\[tan(180{}^\circ -\theta )=-\tan \theta \]
\[cot(180{}^\circ -\theta )=-\cot \theta \]
\[sec(180{}^\circ -\theta )=-\sec \theta \]
\[cosec\,(180{}^\circ -\theta )=+co\sec \theta \]
\[180{}^\circ +\theta \to \] 3rd quadrant
\[\sin \,(180{}^\circ +\theta )=-\sin \theta \]
\[\cos \,(180{}^\circ +\theta )=-\cos \theta \]
\[\tan \,(180{}^\circ +\theta )=+\tan \theta \]
\[270{}^\circ -\theta \to \] 3rd quadrant
\[270{}^\circ +\theta \to \]4th quadrant
\[(-\theta )\to \] 4th quadrant
Similarly, we can find the other allied angles.
Let A, B and C be angles let \[A\pm B\] or \[B\pm C,\] \[C\pm A,\]or \[A+B\pm C\] is said to be compound angles.
Some basic result of compound angles:
\[\sin \,(A+B)=\sin A.\operatorname{cosB}+\cos A\sin B\] .......... (1)
\[\sin \,(A-B)=\sin A.\operatorname{cosB}-\cos A\sin B\] .......... (2)
\[cos(A+B)=\cos A.\operatorname{cosB}-\sin A\sin B\] .......... (3)
\[cos(A-B)=\cos A.\operatorname{cosB}+\sin A\sin B\] .......... (4)
Similarly,
\[\tan \,(A+B)=\frac{\tan A+\operatorname{tanB}}{1+\tan A.\tan B}\] .......... (5)
\[\tan \,(A-B)=\frac{\tan A-\operatorname{tanB}}{1+\tan A.\tan B}\] .......... (6)
\[\cot \,(A+B)=\frac{\operatorname{cotA}.cotB-1}{\cot B+\cot A}\] .......... (7)
\[\cot \,(A-B)=\frac{\operatorname{cotA}.cotB+1}{\cot B-\cot A}\] .......... (8) \[\left. \begin{matrix}
\sin (A+B).\sin (A-B)={{\sin }^{2}}A-{{\sin }^{2}}B \\
={{\cos }^{2}}B-{{\cos }^{2}}A \\
\cos (A+B).\cos (A-B)={{\cos }^{2}}A-{{\sin }^{2}}B \\
={{\cos }^{2}}B-{{\sin }^{2}}A \\
\end{matrix} \right\}\]…… (9)
\[\tan (A+B+C)=\frac{\begin{matrix}
\tan A+\tan B+\tan C \\
-\tan A.\tan B.\tan C \\
\end{matrix}}{\begin{matrix}
1-\tan A.\tan B \\
-\tan B.\tan C-\tan C.\tan A \\
\end{matrix}}\]
\[\left. \begin{matrix}
\sin (A+B+C)=\sin (A+B+C)=sinA.cosB \\
.\cos C+\cos A.\sin B.\cos C \\
+\cos A.\cos B.\sin C \\
-\sin A.\sin B.\sin C \\
\end{matrix} \right\}\]
Similarly,
\[\cos (A+B+C)=\cos A.\cos B.\cos C-\cos A.sinB.sinC-\sin A.\cos B.\cos C\]
Let OX be a fixed line. OY be revolving line such that \[\angle XOY=A\] and OZ makes angle with angles OY is B. i.e. \[\angle YOZ=B\]
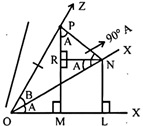
Taking a point P on OZ. we draw, \[PM\bot OX\] and\[PN\bot OY\]. From N we draw \[NL\bot OX\] and draw \[NR\parallel OX\]
\[\because \angle XOY=A\] and \[\angle YOZ=B\]
Then \[\angle XOZ=A+B\]
In DPOM
\[\sin (A+B)=\frac{P}{h}=\frac{PM}{OP}\]
\[=\frac{PR+RM}{OP}=\frac{PR}{OP}+\frac{RM}{OP}\]
\[=\frac{PR}{PN}\times \frac{PN}{OP}+\frac{NL}{ON}\times \frac{ON}{OP}\] \[[\because RM=NL]\]
\[=\cos A\times \sin B+\sin A\times \cos B.\]
\[\sin (A+B)=\sin A.\cos B+\cos A.\sin B.\]
Similarly, other resultants can be proved.
2A, 3A, 4A, i.e. nA is known as the multiple angles of angle A
\[\because \]from compound angle,
\[\sin (A+B)=\sin A.\cos B+\cos A.\sin B\]
Putting \[B=A,\] we have
\[\sin (A+A)=\sin A.\operatorname{cosA}+\cos A.\operatorname{sinA}\]
\[\sin 2A=2.sinA.cosA\]
Similarly,
\[cos(A+B)=\cos A.\operatorname{cosB}-\sin A.\operatorname{sinB}\]
Replacing B by A, we have
\[cos(A+A)=\cos A.\operatorname{cosA}-\sin A.\operatorname{sinA}\]
\[\cos 2A={{\cos }^{2}}A-{{\sin }^{2}}A\]
\[=1-{{\sin }^{2}}A-{{\sin }^{2}}A\]
\[\cos 2A=1-2{{\sin }^{2}}A\]
\[={{\cos }^{2}}A-(1-{{\cos }^{2}}A)\]
\[\cos 2A=2{{\cos }^{2}}A-1\]
Similarly, \[\tan 2A=\frac{2\tan A}{1-{{\tan }^{2}}A}\]
\[\because \tan (A+B)=\frac{\tan A+\tan B}{1-\tan A\tan B}\]
\[\cot 2A=\frac{{{\cot }^{2}}A-1}{2.\cot A}\]
sin2A and cos2A in form of tanA
\[\sin 2A=\frac{2.\sin A.\cos A}{1}=\frac{2\sin A.\operatorname{cosA}}{{{\cos }^{2}}A+{{\sin }^{2}}A}\]
Dividing numerator and denominator by \[{{\cos }^{2}}A\]
\[=\frac{\frac{2\sin A.\operatorname{cosA}}{{{\cos }^{2}}A}}{\frac{{{\cos }^{2}}A+{{\sin }^{2}}A}{{{\cos }^{2}}A}}=\frac{2.\tan A}{1+{{\tan }^{2}}A}\]
\[\sin 2A=\frac{2\tan A}{1+{{\tan }^{2}}A}\]
Similraly, \[\cos 2A=\frac{{{\cos }^{2}}A-{{\sin }^{2}}A}{1}=\frac{{{\cos }^{2}}A-{{\sin }^{2}}A}{{{\cos }^{2}}A+{{\sin }^{2}}A}\]
Dividing numerator and denominator by\[{{\cos }^{2}}A\].
\[\cos 2A=\frac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}\]
Transformation formula
putting \[A+B+C\] (a)
and \[A-B=D\] (b)
Adding we have,
\[2A=C+D\Rightarrow A=\frac{C+D}{2}\Rightarrow B=\frac{C-D}{2}\]
From (1) and (2), we have
\[\sin C+\sin D=2.\sin \frac{C+D}{2}.\cos \frac{C-D}{2}\]
\[\sin C-\sin D=2.cos\frac{C+D}{2}.sin\frac{C-D}{2}\]
From (3) and (4), we have
\[\cos C+\cos D=2.\cos \frac{C+D}{2}.\cos \frac{C-D}{2}\]
\[\cos C-\cos D=-2.sin\frac{C+D}{2}.sin\frac{C-D}{2}=2.\sin \frac{C+D}{2}.\sin \frac{D-C}{2}\]
An angles \[\frac{A}{n},\] \[n\in I,\] is said to be submultiple angle of angle A.
e.g. \[\frac{A}{2},\frac{A}{3},\frac{A}{4}\]….. etc.
\[\because \] By multiple angle
\[\sin 2A=2.sinA.cosA\]
Putting \[\frac{A}{2}\]in place of A
\[\sin 2\times \frac{A}{2}=2.\sin \frac{A}{2}.cos\frac{A}{2}\]
\[\sin A=2.\sin \frac{A}{2}.\cos \frac{A}{2}\]
Similarly, \[\cos A={{\cos }^{2}}\frac{A}{2}-{{\sin }^{2}}\frac{A}{2}=2{{\cos }^{2}}\frac{A}{2}-1=1-2{{\sin }^{2}}\frac{A}{2}\]
\[1+\cos A=2{{\cos }^{2}}\frac{A}{2}\]
\[1-\cos A=2{{\sin }^{2}}\frac{A}{2}\]
\[{{\tan }^{2}}\frac{A}{2}=\frac{{{\sin }^{2}}\frac{A}{2}}{{{\cos }^{2}}\frac{A}{2}}=\frac{1-\cos A}{1+\cos A}\]
\[\tan \frac{A}{2}=\sqrt{\frac{1-\cos A}{1+\cos A}}\]
sin3A. angles in term of A,
\[\sin 3A=\sin (2A+A)\]
\[=\sin 2A.\cos A+\sin A.\cos 2A\]
\[=2.\sin A.\operatorname{cosA}.cosA+sinA.(1-2si{{n}^{2}}A)\]
\[=2.\sin A(1-{{\sin }^{2}}A)+\sin A-2{{\sin }^{3}}A\]
\[=2\sin A-2{{\sin }^{3}}+\sin A-2{{\sin }^{3}}A\]
\[{{\sin }^{3}}A=3\sin A-4{{\sin }^{3}}A\]
\[4{{\sin }^{3}}A=3\sin A-\sin 3A\]
\[{{\sin }^{3}}A=\frac{3\sin A-\sin 3A}{4}\]
\[\cos 3A=4{{\cos }^{3}}A-3\cos A\]
\[4{{\cos }^{3}}A=\cos 3A+3\cos A\]
\[4{{\cos }^{3}}A=\cos 3A+3\cos A\]
and \[\tan 3A=\frac{3\tan A-{{\tan }^{3}}A}{1-3{{\tan }^{2}}A}\]
e.g. \[\sin 15{}^\circ =\sin (45{}^\circ -30{}^\circ )\]
\[=\sin 45{}^\circ .\cos 30{}^\circ -\sin 30{}^\circ .\cos 45{}^\circ =\frac{1}{\sqrt{2}}\times \frac{\sqrt{3}}{2}-\frac{1}{2}.\frac{1}{\sqrt{2}}\]
\[\sin 15{}^\circ =\frac{\sqrt{3-1}}{2\sqrt{2}}\]
e.g. \[\sin 75=\sin (45{}^\circ +30{}^\circ )\]
\[=\sin 45{}^\circ .\cos 30{}^\circ +\sin 30{}^\circ .\cos 45{}^\circ =\frac{1}{\sqrt{2}}\times \frac{\sqrt{3}}{2}+\frac{1}{2}.\frac{1}{\sqrt{2}}\]
\[\sin 75{}^\circ =\frac{\sqrt{3}+1}{2\sqrt{2}}\]
(a) \[\sin 22\frac{1}{2}\]
(b) \[\cos \,\,105{}^\circ \]
(c) \[\tan \,\,15{}^\circ \]
(d) \[\tan 7\frac{1}{2}\]
(e) \[\sin \,\,18{}^\circ \]
(f) \[\cos \,\,36{}^\circ \]
(g) \[\cos 22\frac{1}{2}\] etc.
You need to login to perform this action.
You will be redirected in
3 sec
