Notes - Mathematics Olympiads - Three Dimensional Plane
Category : 11th Class
Three Dimensional Plane
In three dimensional Geometry, it is not a new geometry though it is the refined or extension form of the two dimension geometry. In 3-dimensional geometry. Three axes i.e. x-axis, y-axis and z-axis are perpendicular to each other is considered.
Let \[X'OX',Y'OY\] & \[Z'OZ\] be three mutually perpendicular lines which be intersect at 0. It is called origin.
\[X'OX\xrightarrow{{}}x-axis\]
\[Y'OY\xrightarrow{{}}y-axis\]
\[Z'OZ\xrightarrow{{}}z-axis\]
Plane XOY is called xy plane
YOZ is called yz plane
and ZOX is called zx plane
In 3-D, there are 8 quadrents
Equation of x-axis be y= 0 & z =0
Equation of y-axis be x = 0 & z = 0
and equation of z-axis be x=0 & y=0
Note: In 3-D, a straight line is represented by two equations where as a plane is represented by single equation in at most three variables.
\[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}\]
e.g. Let two points are A (2, 3, 1) & B = (- 5, 2-1)
\[\therefore \,\,\,\,AB=\sqrt{{{(-5-2)}^{2}}+{{(2-3)}^{2}}+{{(-1-1)}^{2}}}\]
\[=\sqrt{49+5}=\sqrt{54}\]
\[P=\left( \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n},\frac{m{{z}_{2}}+n{{z}_{1}}}{m+n} \right)\]
The co-ordinate of the point P dividing the line joining \[A({{x}_{1}},\,{{y}_{1}},\,{{z}_{1}})\] and \[({{x}_{2}},\,{{y}_{2}},\,{{z}_{2}})\] in the ratio m:n externally are
\[P=\left( \frac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\frac{m{{y}_{2}}-n{{y}_{1}}}{m-n},\frac{m{{z}_{2}}-n{{z}_{1}}}{m-n} \right)\]
Midpoint of AB be
\[P=\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2},\frac{{{z}_{1}}+{{z}_{2}}}{2} \right).\]
e.g. Find the co-ordinate of the point which divides the line segment joining the point (-2, 3, 5) & (1, - 4, 6) in the ratio (i) 2: 3 internally (ii) 2:3 externally.
Sol. Here, Let A= (-2, 3, 5) & B= (1, -4, 6)
and m:n =2:3 internally
Let P divides AB in the ratio m: n internally
\[\therefore \,\,\,P=\left( \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n},\frac{m{{z}_{2}}+m{{z}_{1}}}{m+n} \right)\]
\[=\left( \frac{2.1+3(-2)}{2+3},\frac{2(-4)+3.3}{2+3},\frac{2\times 6-3\times 5}{2+3} \right)\]
\[=\left( \frac{-4}{5},\frac{1}{5},\frac{27}{5} \right)\]
When P divides AB in the ratio m : n externally
\[\therefore \,\,\,P=\left( \frac{2.1-3(-2)}{2-3},\frac{2(-4)-3.3}{2-3},\frac{2\times 6-3\times 5}{2-3} \right)\]
\[P=(-8,+17,3).\]
\[A({{x}_{1}},\,{{y}_{1}},\,{{z}_{1}}),\] \[B({{x}_{2}},\,{{y}_{2}},\,{{z}_{2}}),\] & \[C({{x}_{2}},\,{{y}_{2}},\,{{z}_{3}}),\] are
\[\left( \frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3},\frac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3} \right)\]
\[\left( \frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}}{4},\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}+{{y}_{4}}}{4},\frac{z1+z2+z3+z4}{4} \right)\]
Find the co-ordinate of the point R.
Sol: Let \[P(2,-3,4)\] and \[Q(8,0,1,0).\]
Let R divides PQ in the ratio l: 1 internally
\[\therefore \,\,\,\,R=\left( \frac{8\lambda +2}{\lambda +1},\frac{0.\lambda +(-3)}{\lambda +1},\frac{10\lambda +1\times 4}{\lambda +1} \right)\]………… (1)
Here x co-ordinate =4
\[\therefore \,\,\,\,\frac{8\lambda +2}{\lambda +1}=\frac{4}{1}\]
\[\Rightarrow \,\,8\lambda +2=4\lambda +4\]
\[\Rightarrow \,\,8\lambda -4\lambda =4-2=2\]
\[\Rightarrow \,\,4\lambda =2\]
\[\lambda =\frac{2}{4}=\frac{1}{2}\]
Putting the value of \[\lambda \] in (1), we have
\[R=\left( \frac{4+2}{\frac{1}{2}+1},\frac{-3}{\frac{1}{2}+1},\frac{5+4}{\frac{1}{2}+1}, \right)\]
\[=\left( 6\times \frac{2}{3},-3\times \frac{2}{3},9\times \frac{2}{3} \right)=(4,-2,6)\]
Sol: Let \[R=(0,\,b,\,0)\] on y-axis.
Given \[P(3,-2,5)\] & \[PR=5\sqrt{2}\]
By distance formula,
\[PR=\sqrt{{{(3-0)}^{2}}+{{(-2-b)}^{2}}+{{(5-0)}^{2}}}=5\sqrt{2}\]
squaring both side, we have
\[9+{{(2+b)}^{2}}+25=25\times 2\]
\[9+4+{{b}^{2}}+4b+25=50\]
\[\Rightarrow {{b}^{2}}+4b+38-50=0\]
\[(b+6)(b-2)=0\]
\[\Rightarrow b=2,-6\]
Hence b =2 (b=-6 is not possible)
\[\therefore \,\,\,R=(0,2,0)\]
\[=\cos \beta \] and \[n=\cos \,\,\gamma \]
\[\Rightarrow \,\,\,{{\ell }^{2}}+{{m}^{2}}+{{n}^{2}}=1\]
Direction Ratio: The three number a, b, c proportional to the direction cosines \[\ell \], m, n of a vector are known as the direction ratio of the OP vector,
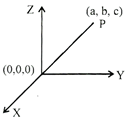
We consider P (a, b, c) be any point in the space length f from the origin to the axis is said to be direction ratio.
\[\therefore \,\,\,\,OP=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\] (By distance formulae)
\[\left| \,r\, \right|=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\]
Note: Direction cosine is proportional to the direction ratio. Let a, b, c be d.r. of the line OP and its d.c. be \[\ell \], m and n respectively.
Then \[\frac{\ell }{a}=\frac{m}{b}=\frac{n}{c}=K\] (say)
Convection from d.r. to D.C.
\[\ell =\pm \frac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]
\[m=\pm \frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]
and \[n=\pm \frac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]
If \[\overline{r}=a\overline{i}+b\overline{j}+c\overline{z}\]
Then a, b and c be the d.r. of r and d.c. of r be
\[\ell =\frac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},m=\frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\] and \[n=\frac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]
\[\frac{{{x}_{2}}-{{x}_{1}}}{\left| PQ \right|},\frac{{{y}_{2}}-{{y}_{1}}}{\left| PQ \right|},\frac{{{z}_{2}}-{{z}_{1}}}{\left| PQ \right|}\] respectively
If \[\theta \] be the angle between two vectors whose direction cosines are \[{{\ell }_{1}},\,{{m}_{1}},\,{{n}_{1}}\]and \[{{\ell }_{2}},\,{{m}_{2}},\,{{n}_{2}}\] then
\[\cos \theta ={{\ell }_{1}}{{\ell }_{2}}+{{m}_{1}}{{m}_{2}}+{{n}_{1}}{{n}_{2}}\]and
\[\sin \theta =\sqrt{{{({{m}_{1}}{{n}_{2}}-{{m}_{2}}{{n}_{1}})}^{2}}+{{({{m}_{1}}{{\ell }_{2}}-{{m}_{2}}{{\ell }_{1}})}^{2}}+{{({{\ell }_{1}}{{n}_{2}}-{{\ell }_{2}}{{n}_{1}})}^{2}}}\]
Then both vection be orthogonal.
Then both vectors are parallel.
If \[\overline{a}={{a}_{1}}\overline{i}+{{b}_{1}}\overline{j}+{{c}_{1}}\overline{k}\]
and \[\overline{b}={{a}_{2}}\overline{i}+{{b}_{2}}\overline{j}+{{c}_{2}}\overline{k}\] be two vectors
\[\therefore \] Its direction ratios be \[{{a}_{1}},\,{{b}_{1}},\,{{c}_{1}}\] and \[{{a}_{2}},\,{{b}_{2}},\,{{c}_{2}}\] respectively, q is the angle between these two vectors. Then
\[\therefore \,\,\,\,\,\,\cos \theta =\frac{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}}{\sqrt{{{a}^{2}}_{1}+{{b}^{2}}_{1}+{{c}^{2}}_{1}}.\sqrt{{{a}^{2}}_{2}+{{b}^{2}}_{2}+{{c}^{2}}_{2}}}.\]
If two vectors are orthogonal then
\[{{a}_{1}}.{{a}_{2}}+{{b}_{1}}.{{b}_{2}}+{{c}_{1}}.{{c}_{2}}=0\]
If two vectors are parallel then \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\]
as \[({{x}_{2}}-{{x}_{1}}).\ell +({{y}_{2}}-{{y}_{1}}).m+({{z}_{2}}-{{z}_{1}}).n\]
Sol. Here P= (1, 1, 2), Q= (3, 4, 1)
Given d.r. = (2, 3, 6)
1st of all we have to find the d.c.
\[\therefore \,\,\,\,\,\,\ell =\frac{2}{\sqrt{{{2}^{2}}+{{3}^{2}}+{{6}^{2}}}}=\frac{2}{7}\]
\[m=\frac{3}{4}\] and \[n=\frac{6}{7}\]
\[\therefore \] Projection of the line joining the points (1, 1, 2) and (3, 4, 1) an the line whose d.c. be \[\left( \frac{2}{7},\frac{3}{7},\frac{6}{7} \right)\] is written as
\[=(3-1)\times \frac{2}{7}+(4-1)\times \frac{3}{7}+(1-2)\times \frac{6}{7}=2\times \frac{2}{7}+3\times \frac{3}{7}+\frac{-6}{7}\]
\[=\frac{4+9-6}{7}=\frac{7}{7}=1\]
You need to login to perform this action.
You will be redirected in
3 sec
