Notes - Mathematics Olympiads - Relation and Function
Category : 11th Class
Relation and Function
Let \[A=\{1,\,2,\,3,4,\}\], \[B=\{2,\,3\}\]
\[A\times B=\{1,\,2,3,\,4,\}\times \{2,3\}=\{(1,2),(2,2),(3,2),(4,2),(1,3),(2,3),(3,3),(4,3)\}\]
Let we choose an arbitrary set:
\[R=[(1,2),(2,2),(1,3),(4,3)]\]
Then R is said to be the relation between a set A to B.
Definition
Relation R is the subset of the Cartesian Product\[A\times B\]. It is represented as \[R=\{(x,y):x\in A\,\] and \[y\in B\}\] {the 2nd element in the ordered pair (x, y) is the image of 1st element}
Sometimes, it is said that a relation on the set A means the all members / elements of the relation
R be the elements / members of \[A\text{ }\times \text{ }A\].
e.g. Let \[A=\{1,\,2,\,3\}\] and a relation R is defined as \[R=\{(x,y):x<y\] where \[x,y\in A\}\]
Sol. \[\because \]\[\mathbf{A=\{1,}\,\mathbf{2,}\,\mathbf{3\}}\]
\[A\times A=\{(1,1),(2,2),(3,3),(2,1),(3,1),(1,2),(3,2),(1,3),(2,3)\}\]
\[\because \,\,\,\,R=\,\,\,\because x<y\]
\[\because \,\,\,\,R=\{(x,y):x<y,and\,x,y\in A\}=\{(1,2),(2,3),(1,3)\]
Note: Let a set A has m elements and set B has n elements. Then \[n(A\times B)\] be \[m\times n\]elements so, total number of relation from A to B or between A and B be\[{{2}^{m\times n}}\].
Types of Relation
e.g. \[\Rightarrow \,\,A=\{1,\,2,\,3,\,4\}\]
\[R=\{(1,\,3),(1,1),(2,3),(3,2),(2,2),(3,1),(3,3),(4,4)\}\]is a reflexive relation on f.
Sol. Yes, because each and every element of A is related to itself in R.
i.e. \[x\,R\,y\Rightarrow y\,R\,x\,\,\forall \,\,x,y\in A\]
\[\because \] xRy is read as x is R-related to y.
i.e. \[xRy\] and \[yRz\Rightarrow xRz\,\,\forall \,\,x,\,y,\,z\in R\].
\[A\times A=\{(1,,1),(2,1),(3,1),(4,1),(1,2),(2,2),(3,2),(4,2),(1,3),(2,3),(3,3),(4,3),(1,4),(2,4),(3,4),(4,4),\]
\[{{R}_{1}}=(1,1),(2,2),(3,2),(2,3),(3,3),(4,4)\]
\[{{R}_{2}}=(2,2),(1,3),(3,3),(3,1),(1,1)\]
\[{{R}_{3}}=(1,1),(2,2),(3,4),(3,3),(4,4)\]
State about\[{{\mathbf{R}}_{\mathbf{1}}}\], \[{{\mathbf{R}}_{\mathbf{2}}}\] and\[{{\mathbf{R}}_{\mathbf{3}}}\]. Are they reflexive, symmetric, anti-symmetric or transitive relations?
Sol. \[{{R}_{1}}\] is symmetric as well as transitive relation for \[{{R}_{2}}\].
\[{{R}_{2}}\]is not reflexive because \[(4,4)\in {{R}_{2}}\] But \[{{R}_{2}}\] is symmetric as well as transitive.
Now,
\[{{R}_{3}}\]is reflexive as well as anti-symmetric because \[(3,4)\in {{R}_{3}}\] but \[(4,3)\notin {{R}_{3}}\].
A relation R on a set A is said to be an equivalence relation on A iff
(i) It is reflexive i.e. \[(x,y)\in R\,\,\forall \,\,x\in R\]
(ii) It is symmetric i.e. \[(x,y)\in R\]
\[\Rightarrow (x,y)\in R\,\,\forall \,\,x,y\in R\]
(ii) It is \[(x,y)\in R(y,z)\,\in R\] then \[(x,z)\in R\]
\[\forall \,\,x,y,z\in R\]
e.g. Let \[A=\{x,y,z\}\] and R is defined as \[R=\{(x,y),(y,y),(z,z),(x,y)(y,z)\}\]
Sol. Yes, because R is satisfied reflexive symmetric as well transitivity condition of relation R on A.
(a) Function as an operation.
(b) Function as a relation.
(c) Function as a mapping.
Type of Function
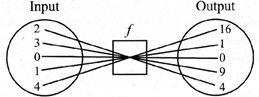
|
Input |
\[f\] |
Output |
e.g. \[y=f(x)\]
\[y=\text{f}\left( x \right)={{x}^{2}}\]
As we know that function contain in the pure mathematics. We cherish both faces of mathematics, the pure as a beautiful retreat from reality and applied an ardent hope for life.
i.e. \[f:A\to B.\] e.g. \[y=f\left( x \right)\]
x is said to be independent variable and y is said to be dependent variable.
All element of set A is said to be domain of f and all elements of set B is said to be co-domain off as well as all image of each element of set A in B, is said to be the range of the function /.
\[y=f(x)\Rightarrow f(A)\subseteq B\]. e.g. \[y=f(A)\le B\].
e.g. \[f:A\to B\]
(i) For every \[x\in A\], \[y\in B\] such that \[y=\text{f}(x)\]. i.e. each element of set A has image in B. But there may be an element in B which is not the image of element of A.
(ii) Same element of A cannot be associated to distinct element of B. i.e. the image of each element of set A has unique. But the distinct element of A may be associated to same element of B.
(i) Into function and onto function (surjective function)
(ii) Into function be two types.
1.a One-one into function (Injective function)
1.b Many-one into function
2.a One-one onto function (bijective function)
2.b Many-one onto function
Function
if\[{{x}_{1}}\ne {{x}_{2}}\Leftrightarrow f\left( {{x}_{1}} \right)\ne f\left( {{x}_{2}} \right)\,\,\forall {{x}_{1}},{{x}_{2}}\in R\].
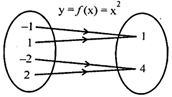
e.g. \[f\,\,\text{: }\,\text{A}\to \text{B}\]is defined as \[\text{y=}(x)={{x}_{2}}\] is a many one function
3. Onto function or surjective function:
e.g. \[\because x\in A\] then \[f\left( x \right)=y\in B\]
iff \[f\left( A \right)=B\]
i.e. range of f= codomain off.
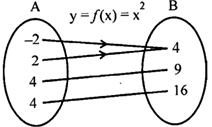
This is onto function.
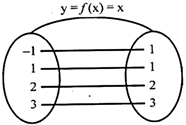
e.g. A function \[f\,\,:\,\,\,A\,\to B\] is defined as \[\text{y=}f(x)=x\] is 1-1 onto function
You need to login to perform this action.
You will be redirected in
3 sec
