11th Class Mathematics Relations and Functions Notes - Mathematics Olympiads - Continuity Differentiability

 

Continuity and Differentiability of a Function

 

Introduction

 

The word 'continuous' means without any break or gap. If the graph a function has no break or gap or jump, then it is said to be continuous. A function which is not continuous is called a discontinuous function. While studying graphs of functions, we see that graphs of functions sinx, x, cosx, etc. are continuous on R but greatest integer functions [x] has break at every integral point, so it is not continuous. Similarly tanx, cotx, seex, 1/x etc. are also discontinuous function on R.

 

Continuous Function

                        

 

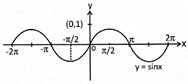
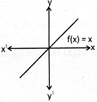
Discontinuous Function

 

                                 

 

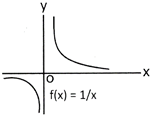
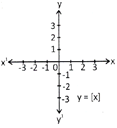
Continuity of a Function at a Point

 

A function f(x) is said to be continuous at a point x = a of its domain if and only if it satisfies the following three condition:

 

(i)         f(a) exist. ('a' line in the domain of f)

(ii)        \[\underset{x+a}{\mathop{\lim }}\,\] f(x) exist e.e; \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\] f(x)= \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\] f(x) or R.H.L= L.H.L

(iii)       \[\underset{x+a}{\mathop{\lim }}\,\] f(x) = f(a) (limit equals the value of function)

 

Continuity from Left and Right

A function f(x) is said to be continuous at a point x = a of its domain if and only if it satisfies the following three condition:

 

(i)         f(a) exist. ('a' line in the domain of f)

(ii)        \[\underset{x+a}{\mathop{\lim }}\,\] f(x) exist e.e; \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\] f(x)= \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\] f(x) or R.H.L= L.H.L

(iii)       \[\underset{x+a}{\mathop{\lim }}\,\] f(x) = f(a) (limit equals the value of function)

 

Cauchy's Definition of Continuity

A function f is said to be continuous at a point a of its domain D if for every \[\varepsilon >o\] there exists \[\delta >o\] (dependent of\[\varepsilon \]) such that \[\left| x-a \right|<\delta \]

\[\Rightarrow \left| \text{f}(x)-\text{f(a)} \right|<\varepsilon \]

 

Comparing this definition with the definition of limit we find that f(x) is continuous at x = a if \[\underset{x\to a}{\mathop{\lim }}\,\]f(x) exists and is equal to f(a) i.e; \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\] f(a) \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\] f(x).

 

Continuity from Left and Right

           

Function f(x) is said to be

 

(i)         Left continuous at x= a if \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\,\,\text{f(x)=f(a)}\text{.}\]

(ii)        Right continuous at x = a if \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\,\,\text{f(x)=f(a)}\text{.}\]

Thus a function f(x) is continuous at a point x = a if it is left continuous as well as right continuous at x = a.

 

 

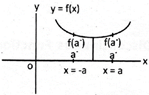
Differentiation

 

The function, f(x) is differentiable at point P, iff there exists a unique tangent at point P. In other words, f(x) is differentiable at point P iff the curve does not have pas a corner point i.e; the function is not differentiable at those point on which function has jumps (or holes) and sharp edges.

Let us consider the function \[\text{f(x)=}\left| x-1 \right|,\]which can be graphically shown.

 

 

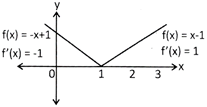
Which show f(x) is not differentiable at x = 1. since f(x) has no edge at x=1.

 

(i)         Right hand derivative: R.H.D. of f(x) at x= a. denoted by

 

\[\text{f }\!\!'\!\!\text{ (a+o)=f }\!\!'\!\!\text{ }({{a}^{+}})=\underset{h\to o}{\mathop{\lim }}\,\frac{\text{f(a+h)-f(a)}}{h}\]

 

(ii)        Left hand derivative: L.H.D. of f(x) at x= a, denoted by

 

\[\text{f }\!\!'\!\!\text{ (a-o)=f }\!\!'\!\!\text{ }({{a}^{-}})=\underset{h\to o}{\mathop{\lim }}\,\frac{\text{f(a-h)-f(a)}}{-h}\]

 

(iii)       A function f(x) is said to be differentiable (finitely) at x = a.

 

if \[\text{f }\!\!'\!\!\text{ (a+o)=f }\!\!'\!\!\text{ }(a-o)=\] finite

 

\[\Rightarrow \underset{h\to o}{\mathop{\lim }}\,\frac{\text{f}(a+h)-f(a)}{h}=\underset{h\to o}{\mathop{\lim }}\,\frac{\text{f}(a-h)-f(a)}{-h}=\] finite and the common limit is called the derivative of f(x) at x=a. denoted by \[f'(a)\].

           

\[\Rightarrow \text{f }\!\!'\!\!\text{ (a)=}\underset{h\to a}{\mathop{\lim }}\,\frac{f(x)-f(a)}{x-9}\] {\[x\to 9\] from the left as well as from the right}.

 

1. Find derivative of y= sin x. by 1st principle

 

Sol:      \[y=\text{f}(x)=sinx\]                             .....(1)

 

Let \[\delta \times \] be the small increasement in \[\times \] then \[\delta y\] be the corresponding increasement in y.

           

\[y=\delta y=sin(x+\delta x)\]                  …..(2)

 

Now (2)-(1), we have

 

\[y+\delta y-y=sin(x+\delta x)-sinx\]

           

\[\delta y=2.\cos \frac{x+\delta x+x}{2}.\sin \left( \frac{x+\delta x-x}{2} \right)\]

 

Dividing dx on both sides and taking limit \[\delta x\to 0,\] we have

           

\[\underset{\delta x\to 0}{\mathop{\lim }}\,\frac{\delta y}{\delta x}=\underset{\delta x\to 0}{\mathop{\lim }}\,2.\frac{\cos \left( \frac{2x+\delta x}{2} \right).\sin \left( \frac{\delta x}{2} \right)}{\delta x}\]

           

\[\frac{dy}{dx}=\underset{\delta x\to 0}{\mathop{\lim }}\,2.\cos \left( x+\frac{\delta x}{2} \right).\left( \frac{\sin \frac{\delta x}{2}}{\frac{\delta x}{2}\times 2} \right)\]

Applying limit \[\delta x\to 0=\cos x\times 1=\cos x\left[ \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \theta }{\theta }=1 \right]\]

 

i.e. \[\frac{d}{dx}(\sin x)=\cos x\]

 

\[\frac{dy}{dx}\]is said to be differential coefficient of y = f(x).

 

It is denoted by \[{{y}_{1}}=\frac{dy}{dx}=\text{f }\!\!'\!\!\text{ (x)}\]

 

• Some Important Formula

 

1. \[\frac{d}{dx}(\sin x)=\cos x\]
2. \[\frac{d}{dx}(cosx)=-\sin x\]

 

3. \[\frac{d}{dx}(tanx)={{\sec }^{2}}x\]
4. \[\frac{d}{dx}(cotx)=-co{{\sec }^{2}}x\]

 

5. \[\frac{d}{dx}(secx)=\sec x\tan x\]
6. \[\frac{d}{dx}(cosecx)=-co\sec x.\cot x\]

 

7. \[\frac{d}{dx}({{x}^{n}})=n{{x}^{n-1}}\]
8. \[\frac{d}{dx}({{e}^{x}})={{e}^{x}}\]

 

9. \[\frac{d}{dx}(logx)=\frac{1}{x},\] for \[x>0\]
10. \[\frac{d}{dx}({{\sin }^{-1}}x)=\frac{1}{\sqrt{1-{{x}^{2}}}},\] for \[-1<\times <1\]

 

11. \[\frac{d}{dx}(co{{s}^{-1}}x)=\frac{-1}{\sqrt{1-{{x}^{2}}}},\]for \[-1<\times <1\]
12. \[\frac{d}{dx}(ta{{n}^{-1}}x)=\frac{1}{1+{{x}^{2}}},\] for \[x\varepsilon R\]

 

13. \[\frac{d}{dx}(x)=1\]
14. \[\frac{d}{dx}(C)=0,\]Where C= any const.

 

15. \[\frac{d}{dx}(\sin ax)=a\cos ax\]
16. \[\frac{d}{dx}({{a}^{x}})={{a}^{x}}.\log a,\] for \[a>0\]

 

• Some Basic Rules

 

1. \[\frac{d}{dx}(u\pm v)=\frac{d}{dx}(u)\pm \frac{d}{dx}(v).\]Where u and v be the function of x.

 

2. \[\frac{d}{dx}(C.u)=C.\frac{d}{dx}(u).\] Where C= any const.

           

e.g. \[\frac{d}{dx}(5{{x}^{2}})=5.\frac{d}{dx}({{\underline{x}}^{2}})\]

 

\[=.5.2.{{(x)}^{2-1}}=10{{x}^{1}}=10x\]

 

3. \[\frac{d}{dx}(u.v)=u.\frac{dv}{dx}+v.\frac{du}{dx},\] e.g. \[\frac{d}{dx}({{e}^{x}}.\sin x)\]

 

\[={{e}^{x}}.\frac{d}{dx}(\sin x)+\sin \frac{d}{dx}({{e}^{x}})={{e}^{x}}\cos x+\sin x\,\,{{e}^{x}}={{e}^{x}}(\cos x+\sin x)\]

 

4. \[\frac{d}{dx}\left( \frac{u}{v} \right)=\frac{v.\frac{du}{dx}-u.\frac{dv}{dx}}{{{v}^{2}}},\] e.g. \[\frac{d}{dx}{{\left( \frac{{{x}^{2}}}{\sin x} \right)}_{v}}^{u}\]

\[=\frac{\sin x\frac{d}{dx}({{\underline{x}}^{2}})-{{x}^{2}}\frac{d}{dx}(\sin x)}{{{\sin }^{2}}x}\]

\[=\frac{d}{dx}({{\log }_{c}}{{a}^{x}})-\frac{d}{d{{x}_{({{a}^{x}})}}}(\log {{a}^{x}}).\frac{d}{dx}({{\underline{a}}^{x}})=\frac{1}{{{a}^{x}}}.{{a}^{x}}.\log a=\log a\]