Notes - Mathematics Olympiads - Circles
Category : 11th Class
Circles
Key Points to Remember
Circle: A circle is the locus of the points which move in the plane such that the its distance from a fixed point always remain constant, is said to be the circle. The fixed point is said to be the centre of the circle and its distance is said to be the radius of the circle.
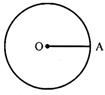
Let C (O, r) is a circle with centre 0 & radius r. A be any point it.
\[\therefore \] OA = radius of the circle
When centre be considered as the origin & radius be a, then equation of the circle is written as \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\]
e.g. find the equation of the circle whose centre is (2, 3) and radius is 6 units
Sol. Let P(x, y) be any point on the circle by distance formula
\[{{(x-2)}^{2}}+{{(y-3)}^{2}}={{(6)}^{2}}\]
\[{{x}^{2}}+{{y}^{2}}-4x-6y+13=36\]
\[{{x}^{2}}+{{y}^{2}}-4x-6y-23=0\]
Which is the required equation of the circle.
Since, the general equation of the second degree be\[a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0\]..... (1)
Condition for the circle.
(i) a = b should be unity
(ii) product of xy term be zero.
Here equation (1) becomes the general equation of the circle.
i.e. The general equation of the circle be written as
\[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]
Its radius \[=\sqrt{{{g}^{2}}+{{\text{f}}^{2}}-c}\] centre of the circle \[\equiv (-g,-\text{f})\]
(i) If \[{{g}^{2}}+{{\text{f}}^{2}}-c>0,\] then equation of the circle represents the real circle with the centre \[(-g,-\text{f}).\]
(ii) If \[{{g}^{2}}+{{\text{f}}^{2}}-c=0\] i.e. radius of the circle is zero. Then the equation of the circle represent point whose co-ordinate be \[(-g,-\text{f}).\]
(iii) If \[{{g}^{2}}+{{\text{f}}^{2}}-c<0\] i.e. radius of the circle is imaginary but its centre, \[(-g,-\text{f}).\] be real. This type of circle is not possible to draw in the plane.
(i) Circle with centre, (a, b) and which touches the x-axis.
Since, the circle touch the x-axis then radius of the circle is equal to the y-ordinate of the centre of the circle.
i.e. Radius of the circle = b
Hence, equation of the circle is
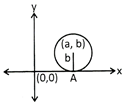
\[{{({{x}^{2}}-a)}^{2}}+{{(y-b)}^{2}}={{b}^{2}}\]
\[{{x}^{2}}+{{y}^{2}}-2ax-2by+{{a}^{2}}+{{b}^{2}}={{b}^{2}}\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2ax-2by+{{a}^{2}}=0\]
(ii) Circle with centre, (a, b) which touches the y-axis.
Since, equation of the circle touches the y- axis. i.e. the radius of the circle is equao to the x- ordinate of the centre of the circle.
i.e. Radius of the circle is
\[{{({{x}^{2}}+a)}^{2}}+{{(y-b)}^{2}}={{a}^{2}}\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2ax-2by+{{a}^{2}}+{{b}^{2}}={{a}^{2}}\]
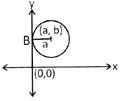
\[{{x}_{2}}+{{y}_{2}}-2ax-2by+{{b}_{2}}=0\]
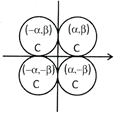
(iii) Circle with radius a and which touches both the coordinate axis.
Since, when centre touches both axis then the magnitude of abscissa and ordinate of the centre be equal i.e. \[c=(\pm \alpha ,\,\beta )\]
Then there are four types of circle, can be formed in this situation
Equation of a circle in Diameter form: Let \[A({{x}_{1}},\,{{y}_{1}})\] & \[B({{x}_{2}},\,{{y}_{2}})\] be the end point of the diameter AB of the circle with centre, C.
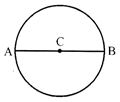
\[\therefore \] Equation of the circle be written as
\[(x-{{x}_{1}})(x-{{x}_{2}})+(y-{{y}_{1}})(y-{{y}_{2}})=0\]
& Its centre \[\equiv \left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
& Its radius \[=\frac{1}{2}\left( \sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}} \right)\]
Sol. Equation of circle when end points of the diameter \[(2,3)\] & \[(-5,1)\] be \[(x-2)(x+5)+(y-3).(y-1)=0\]
\[{{x}^{2}}+3x-10+{{y}^{2}}-4x+3=0\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}+3x-4x-7=0\]
Centre \[\equiv \left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\equiv \left( \frac{2-5}{2},\frac{1+3}{2} \right)\equiv \left( \frac{3}{2},2 \right)\]
radius \[=\sqrt{{{g}^{2}}+{{\text{f}}^{2}}-c}=\sqrt{\frac{9}{4}+4+7}=\sqrt{\frac{53}{4}}=\frac{\sqrt{53}}{2}\]
Let P(x, y) be any point on the circle with centre as the origin. Let radius of the circle, OP = a
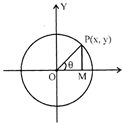
Let OP makes an angle e with the axis. We draw \[PM\bot OX\]
\[x=OM=a.\cos \theta \] & \[y=PM=a.sin\theta \]
Thus, in the parametric form, equation of the circle be
\[x=a.\cos \theta \] & \[y=a.sin\theta \]with the parameter \[\theta \]
Q, Find the parametric representation of the circles:
\[{{\mathbf{x}}^{\mathbf{2}}}\mathbf{+}{{\mathbf{y}}^{\mathbf{2}}}\mathbf{+6x-8y+9=0}\]
Sol: \[{{x}^{2}}+2.3.x+{{(3)}^{2}}+{{y}^{2}}-2.y.4+{{(4)}^{2}}+9=9+16\]
\[{{(x+3)}^{2}}+{{(y-4)}^{2}}=25-9=16\]
\[{{(x+3)}^{2}}+{{(y-4)}^{2}}={{4}^{2}}\]
Here, centre be \[(-3,4)\] & radius =4
So, \[x+3=a.\cos \theta =4.\cos \theta \]
\[\Rightarrow x=-3+4.\cos \theta \]
\[y=4+4\sin \theta =4(1+\sin \theta )\]
(i) The length of the intercept made by the circle
\[{{x}^{2}}+{{y}^{2}}+2gs+2\text{f}y+c=0\]
on x - axis,
\[AB=2\sqrt{{{g}^{2}}-c}\]
& on y-axis \[CD=2\sqrt{{{\text{f}}^{2}}-c}\]
(ii) When the circle touches the x-axis i.e. \[\left| \,\,AB\,\, \right|=0\]
\[\Rightarrow c={{g}^{2}}\]
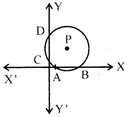
when the circle touches the y-axis.
Then, \[\left| \,CD\, \right|=0\Rightarrow c={{\text{f}}^{2}}\]
(iii) If the circle touches both the axis, then
\[\left| \,AB\, \right|=\left| \,CD\, \right|=0\]
i.e. \[c={{\text{f}}^{2}}={{g}^{2}}\]
(iv) Length of the intercept be always positive
e.g. find the length of the intercept made on the axes by the circle
\[{{x}^{2}}+{{y}^{2}}+8x-10y-16=0\]
Sol. The general equation of the circle be
\[{{x}^{2}}+{{y}^{2}}+2gx+2\operatorname{f}y+c=0\]
Comparision this equation to the given circle, then, we have
\[g=-4\] & \[\text{f}=5,\] \[c=-16\]
\[\therefore \] Intercept on the x-axis intercept
\[=\frac{1}{2}\sqrt{{{g}^{2}}-c}=2\sqrt{16+16}=2.4\sqrt{2}=8\sqrt{2}\]
Intercept on y-axis
\[=2\sqrt{{{\text{f}}^{2}}-c}=2\sqrt{{{(5)}^{2}}+16}=2\sqrt{41}\]
Let \[S\equiv {{x}^{2}}+{{y}^{2}}+2gx+2\text{f}y+c=0\] be a circle and \[P({{x}_{1}},\,{{y}_{1}})\] be any point in the plane when the point
\[P({{x}_{1}},\,{{y}_{1}})\] be outside the circle then
\[S\equiv {{x}_{1}}^{2}+{{y}_{1}}^{2}+2g{{x}_{1}}+2\text{f}{{y}_{1}}+c=0\]
& when the point P(x, y) be inside the circle S;
Then \[S\equiv {{x}_{1}}^{2}+{{y}_{1}}^{2}+2g{{x}_{1}}+2\text{f}{{y}_{1}}+c<0\]
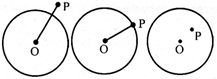
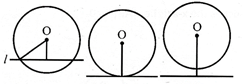
Let C (O, r) be a circle with centre O & radius r. Let \[\ell \] be any line in the plane of the circle & d is the perpendicular length from 0 to the line\[\ell \].then
(a) \[\ell \]intersects the circle C (O, r) in two distinct points iff d < r
(b) \[\ell \] intersect the circle C (Q, r) at one & only one point iff d=r
(c) \[\ell \] doesn't intersect the circle iff d > a.
Length of intercept made by a circle on a line.
Let a line {. meets the circle C (O, r) with centre O & radius r in two distinct points A & B. And d be the
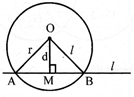
Perpendicular distance from the centre O to the line\[\ell \]. Then length of the intercept made by the circle on the line,
\[\ell =AB=2.AM=2.MB=2\sqrt{{{r}^{2}}-{{d}^{2}}}\]
e.g. Find the length of the chord intercepted by the circle \[{{x}^{2}}+{{y}^{2}}=16\] and the line \[x-y+1=0\]
Sol. Given equation of the circle be
\[{{x}^{2}}{{y}^{2}}={{4}^{2}}\]
So, centre = (0, 0) and radius =4
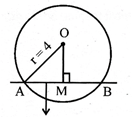
\[x-y-1=0\]
Length of the for distance from O (0, 0) to the line \[x-y+1=0,\] OM
\[=\frac{\left| \,0-0+1\, \right|}{\sqrt{{{1}^{2}}+{{1}^{2}}}}=\frac{1}{\sqrt{2}}\]
\[AM=\sqrt{O{{A}^{2}}-O{{M}^{2}}}=\sqrt{{{4}^{2}}-{{\left( \frac{1}{\sqrt{2}} \right)}^{2}}}\]
\[=\sqrt{16-\frac{1}{2}}=\sqrt{\frac{31}{2}}\]
\[\therefore \] Length of the chord intercepted by
\[x-y+1=0\,\,be=Ab=2.AM=2\sqrt{\frac{31}{2}}=\sqrt{62}\]
Two circles having the centre \[{{c}_{1}}({{x}_{1}},{{y}_{1}})\] & \[{{c}_{2}}({{x}_{2}},{{y}_{2}})\]
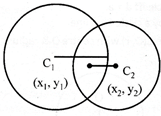
with radii \[{{r}_{1}}\] & \[{{r}_{2}}\] respectively be
\[\left| \,{{r}_{1}}-{{r}_{2}}\, \right|<{{c}_{1}}{{c}_{2}}<{{r}_{1}}+{{r}_{2}}\]
Then
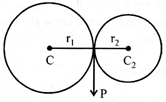
\[{{c}_{1}}.{{c}_{2}}={{r}_{1}}+{{r}_{2}}\]
\[\therefore \,\,\,\,\,\,\,P\equiv \left( \frac{{{x}_{2}}.{{r}_{1}}+{{x}_{1}}.{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}},\frac{{{y}_{2}}.{{r}_{1}}+{{y}_{1}}.{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}} \right)\]
(3)
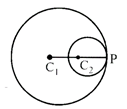
Touch each other internally iff
\[{{c}_{1}}.{{c}_{2}}=\left| \,{{r}_{1}}-{{r}_{2}}\, \right|\]
\[\therefore \,\,\,\,P\equiv \left( \frac{{{r}_{1}}{{x}_{2}}-{{r}_{2}}{{x}_{1}}}{{{r}_{1}}-{{r}_{2}}},\frac{{{r}_{1}}{{y}_{2}}-{{r}_{2}}{{y}_{1}}}{{{r}_{1}}-{{r}_{2}}} \right)\]
(4) One circle lies outside the other if \[AB>{{r}_{1}}+{{r}_{2}}\]
i.e. \[{{c}_{1}}{{c}_{2}}>{{r}_{1}}+{{r}_{2}}\]
(5) One circle be contained in the other circle.
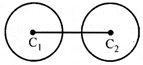
lf \[AB<\left| \,{{r}_{1}}-{{r}_{2}}\, \right|\]
\[{{x}^{2}}+{{y}^{2}}+2gx+2\text{f}y+c=0\] at point \[P({{x}_{1}},{{y}_{1}})\] on it be
\[x.{{x}_{1}}+y.{{y}_{1}}+g(x+{{x}_{1}})+\text{f}(y+{{y}_{1}})+c=0\]
Tips: To obtain the equation of the tangent we replace \[{{x}^{2}}\] by \[x.{{x}_{1}},\,\]\[{{y}^{2}}\,by\,y.{{y}_{1}}\times by\,\frac{x+{{x}_{1}}}{2}\] & \[y\,by\,\frac{y+{{y}_{1}}}{2}\] e.g.
\[y=mx+a\sqrt{1+{{m}^{2}}}\]
& co-ordinate of the point of contact be
\[\left( \frac{\pm am}{\sqrt{1+{{m}^{2}}}}\mp \frac{a}{\sqrt{1+{{m}^{2}}}} \right)\]
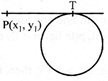
Let \[P(d{{x}_{1}},{{y}_{1}})\] be any point outside the circle \[S=0\,\,S={{x}^{2}}+{{y}^{2}}+2gc+2\text{f}y+c=0\] then the length of the tangent from P to S= 0
\[=\sqrt{{{S}_{1}}}\] e.i. \[PT=\sqrt{{{x}^{2}}_{1}+{{y}^{2}}_{1}+2g{{x}_{1}}+2\text{f}{{y}_{1}}+c}\]
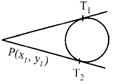
The equation of the pair of tangent drawn from the point \[P({{x}_{1}},{{y}_{1}})\] to the circle
S=0 be
\[S.{{S}_{1}}={{T}^{2}}\]
Where \[S\equiv {{x}^{2}}+{{y}^{2}}+2gx+2\text{f}y+c\]
\[{{S}_{1}}\equiv {{x}^{2}}_{1}+{{y}^{2}}_{1}+2g{{x}_{1}}+2\text{f}{{y}_{1}}+c\]
\[T\equiv x.{{x}_{1}}+y.{{y}_{1}}+g(x+{{x}_{1}})+\text{f}(y+{{\text{f}}_{1}})+c\]
Note: The pair of tengents from (0, 0) to the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2\text{f}y+c=0\] are at right angles if \[{{g}^{2}}+{{\text{f}}^{2}}=2c\]
Direct Comman Tangents: The direct comman tangents to the two circles meet at a point P(say) which lies on the line joining the centres \[{{c}_{1}}\] & \[{{c}_{2}}\] of two circles & divide \[{{c}_{1}}{{c}_{2}}\] externally in the ratio of their raddii \[{{r}_{1}}\] & \[{{r}_{2}}\] (saying)\
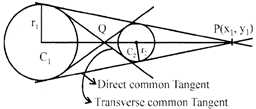
Tips: For direct common tangent
(i) 1st of all, to find the centres \[{{c}_{1}}\] & \[{{c}_{2}}\] and radius \[{{r}_{1}}\] & \[{{r}_{2}}\] of the two given circles respectively.
(ii) Find the disered point \[P({{x}_{1}},{{y}_{1}})\] which divides \[{{c}_{1}}{{c}_{2}}\] in the ratio \[{{r}_{1}}:{{r}_{2}}\] externally.
(iii) Then, write any equation of the st line (1) through the \[P({{x}_{1}},{{y}_{1}}){{r}_{1}}:{{r}_{2}}\] be \[y-{{y}_{1}}=m(x-{{x}_{1}})\]
(iv) Value of m = length of the perpendicular on line (1) from the centre \[{{c}_{1}}={{r}_{1}}\]
(v) Putting the value of m in equation (1), thus, we will find the required equation of direct comman tangent.
(1) We will apply the same processure to find the transverse common tangents....b but in transverse common tangent, p (ln fig. it is Q) divides \[{{c}_{1}}{{c}_{2}}\] internally in the ratio\[{{r}_{1}}:{{r}_{2}}\].
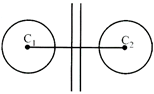
(i) If two circles do not intersect, i.e. \[{{c}_{1}}{{c}_{2}}>{{r}_{1}}+{{r}_{2}}\] then, they have two transverse and two direct common tangents.
(ii) If two circle intersect \[{{c}_{1}}{{c}_{2}}<{{r}_{1}}+{{r}_{2}}\] then they have two direct common tangent only.
(iii) If two circles touch externally \[({{c}_{1}}{{c}_{2}}={{r}_{1}}+{{r}_{2}})\] then they have one trnasverse & two direct common tangents.
(iv) If two circles touch internally \[({{c}_{1}}{{c}_{2}}={{r}_{1}}-{{r}_{2}})\] then they have only one common tangents.
Image to the circle by the line mirror.
\[ax+by+c=0\]
Let the circle be
\[S={{x}^{2}}+{{y}^{2}}+2gx+2\text{f}y+c=0\] ..... (1)
and the line be
\[ax+by+c=0\] ..... (2)
In image to the circle, the radius of image circle unalter but centre changes. Let the centre of the this circle be \[({{x}_{1}},{{y}_{1}})\] then slope of \[{{c}_{1}}{{c}_{2}}\,\,\times \] slope of line (2) = 1 then midpoint of the \[{{c}_{1}}(-g,-\text{f})\] & \[{{c}_{2}}({{x}_{1}},{{y}_{1}})\] lies on the line \[ax+by+c=0\]
i.e. \[a.\left( \frac{{{x}_{1}}-g}{2} \right)+b.\frac{({{y}_{1}}-\text{f})}{2}+c=0\] ...... (3)
Solving equation (2) & (3), we can obtain the value of \[({{x}_{1}},{{y}_{1}})\]
Thus, the required image circle be
\[{{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}={{r}^{2}}\]
where \[r=\sqrt{{{g}^{2}}+{{\text{f}}^{2}}-c}\]
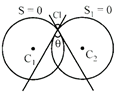
Let q be the angle between two circles
\[S\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{\text{f}}_{1}}y+{{c}_{1}}=0\]
\[S'={{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{\text{f}}_{2}}y+{{c}_{2}}=0\]
Then
\[\cos \theta =\pm \frac{2{{g}_{1}}.{{g}_{2}}+2{{\text{f}}_{1}}.{{\text{f}}_{2}}-{{c}_{1}}-{{c}_{2}}}{2.\sqrt{{{g}^{2}}_{1}+{{\text{f}}^{2}}_{1}-{{c}_{1}}}\sqrt{{{g}^{2}}_{2}+{{\text{f}}^{2}}_{2}-{{c}_{2}}}}\]
Case- l : If \[\theta =90{}^\circ \]
Then, \[2{{g}_{1}}.{{g}_{2}}+2{{\text{f}}_{1}}.{{\text{f}}_{2}}={{c}_{1}}+{{c}_{2}}\]
i.e. this intersection is said to be orthogonal intersection of two circles.
Equation of the family of the circles passing through two given points \[({{x}_{1}},{{y}_{1}})\] & \[({{x}_{2}},{{y}_{2}})\] is
\[(x-{{x}_{1}})(x-{{x}_{2}})+(y-{{y}_{1}})(y-{{y}_{2}})+\]
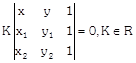
& K be obtained from the 3rd condition.
You need to login to perform this action.
You will be redirected in
3 sec
