Quadratic Inequation
Category : 10th Class
QUADRATIC INEQUATION
FUNDAMENTALS
Quadratic In equations
Consider the quadratic equation\[a{{x}^{2}}+bx+c=0.\,\,\,(a\ne 0)\]where a, b, and c are real numbers.
The quadratic in equations related to \[a{{x}^{2}}+bx+c=0\]are \[a{{x}^{2}}+bx+c<0\]and \[a{{x}^{2}}+bx+c>0\].
Assume that a > 0 (This assumption is always valid because if a<0, we can always multiply the in equation by (– 1) to get a > 0.)
For example, \[-2{{x}^{2}}+3x+2<0\]can be written as \[-2{{x}^{2}}-3x-2>0\]
Note: The change in the sign of the inequality, when it is multiplied by (– 1).
Then following cases arise:
Case – 1: If\[{{b}^{2}}-4ac>0\], then the equation \[a{{x}^{2}}+bx+c=0\]has real and unequal roots. Let \[\alpha \]and \[\beta (\alpha <\beta )\]be the roots. Then,
\[\therefore a{{x}^{2}}+bx+c=a(x-\alpha )(x-\beta )\]
![]()
\[\therefore a{{x}^{2}}+bx+c>0\]
\[\therefore a{{x}^{2}}+bx+c<0\]
\[\therefore a{{x}^{2}}+bx+c>0\]
Case – 2: If\[{{b}^{2}}-4ac=0\], then \[a{{x}^{2}}+bx+c=0\]has real and equal roots.
Let \[\alpha \] be the equal roots.\[\Rightarrow a{{x}^{2}}+bx+c=a(x-\alpha ')(x-\alpha ')\]
If\[x<\alpha '\]. Then, \[(x-\alpha ')<0\]. \[\therefore a{{x}^{2}}+bx+c>0\].
However, if\[x>\alpha '\], then,\[\left( x-\alpha ' \right)>0\].
\[\therefore a{{x}^{2}}+bx+c>0\].
Case – 3: If\[{{b}^{2}}-4ac<0\], then \[a{{x}^{2}}+bx+c=0\]has no real roots.
In this case, \[a{{x}^{2}}+bx+c>0,\forall x\in R\].
The above three cases (case 1 to case 3) may be summarized as:
Sample Question: Solve the in equation\[{{x}^{2}}-7x+12<0\].
Solution: Given in equation is \[{{x}^{2}}-7x+12<0\Rightarrow {{x}^{2}}-3x-4x+12<0\]
\[\Rightarrow \left( x-3 \right)\left( x-4 \right)<0;\Rightarrow \left( x-3 \right)<0\] and \[\left( x-4 \right)>0\]……………..(1)
Or. \[\left( x-3 \right)>0\] and \[\left( x-4 \right)<0\]…………...(2)
In set notation, ‘and’ means intersection whereas ‘or’ means UNION.
From (1), x < 3 and x > 4
\[\therefore \] There is not overlap and this is a NULL set \[\phi \]………. (1)
From \[\left( 2 \right),x>3\] and \[x<4\Rightarrow x\in (3,\infty )\cap x\in (-\infty ,4)\Rightarrow x\in (3,4)\]
Clearly, the intersection set is (3, 4)
Finally, we have union of NULL set \[\phi \] in equation (1) and (3, 4) in equation (2) \[\Rightarrow \]
Solution \[=\phi \cup (3,4)=(3,4)\]
Elementary Questions -1
Solve for \[x:{{x}^{2}}-3x+2\ge 0\]
Solution:
Given in equation is \[{{x}^{2}}-3x+2\ge 0\].
\[\Rightarrow (x-1)(x-2)\ge 0\Rightarrow x-1\ge 0\] and \[x-2\ge 0\] or \[x-1\le 0\]and \[x-2\le 0\]
\[\Rightarrow x\ge 1\]and \[x\ge 2\Rightarrow x\in [1,\infty ]\cap [2,\infty )\Rightarrow x\in [2,\infty )\]…………..(1)
Or,
\[x\le 1\]and \[x\le 2\Rightarrow x\in [-\infty ,1)\cap [-\infty ,2)\Rightarrow x\in (-\infty ,1]\].............(2)
(1) & (2) are combined as \[x\in (-\infty ,1]\cup [2,\infty )\]
Hence, the solution for the given in equation is \[x\in (-\infty ,1]\cup [2,\infty )\].
This can be seen on number line as follows:
From \[(1);x\in [2,\infty )\]
![]()
OR,
From \[(2);x\in (-\,\infty ,1]\]
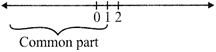
OR, means UNION\[\Rightarrow x\in (-\infty ,1]\cup [2,\infty )\].
Mod Function
\[y=f(x)=|x|\]is called mod x or mod of x;
Mod of x is defined as, |x| = x when\[x\ge 0\]; And |x| = – x when\[x\le 0\]
Thus, mod of x is a always + ve value of x.
Elementary question
Find range of \[y=|x+2|\]when \[x\in (-5,-1)\]
Answer: \[x>-5\therefore y=x+2>-3\] \[(when\,\,|x+2|=x+2)\]
Also \[x<-1\Rightarrow x+2<+1;\] \[\therefore y=x+2\in (-3,+1)\]
Other case: When \[y=|x+2|=-x-2;\,\,x>-5\Rightarrow -x<+5\Rightarrow -x-2<+3\]
\[x<-1\Rightarrow -x>+1\Rightarrow -x-2>-1;\] Thus \[y=-x-2\in (-1,3)\]
or, \[x+2\in (-3,0]\cup [0,1);\] \[\therefore |x+2|\in (0,+3)\cup [0,1]=[0,3)\]
Graph of |x|
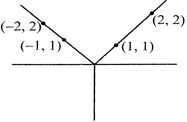
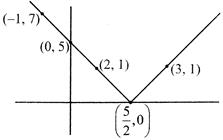
Elementary question: Draw graph of |2x – 5|
You need to login to perform this action.
You will be redirected in
3 sec
