10th Class Mathematics Polynomials Polynomial

Polynomial

Category : 10th Class

POLYNOMIAL

FUNDAMENTALS

Polynomial: A function p(x) of the form \[p(x)={{a}_{0}}+{{a}_{1}}{{x}^{n}}+......+{{a}_{n}}{{x}^{n}},\]where \[{{a}_{0}},{{a}_{1}},.......{{a}_{n}}\]an are real numbers and ‘n’ is a non-negative (positive) integer is called a polynomial.

Note: \[{{\mathbf{a}}_{\mathbf{0}}}\mathbf{,}{{\mathbf{a}}_{\mathbf{1}}}\mathbf{,}.....{{\mathbf{a}}_{\mathbf{n}}}\] are called the coefficients of the polynomial.

If the coefficients of a polynomial are integers, then it is called a polynomial over integers.
If the coefficients of a polynomial are rational numbers, then it is called a polynomial over rational numbers.
If the coefficients of a polynomial are real numbers, then it is called a polynomial over real numbers.
A function \[p(x)={{a}_{0}}+{{a}_{1}}x+........+{{a}_{n}}{{x}^{n}}\] is not a polynomial if the power of the variable is either negative or a fractional number.
Standard form: A polynomial is said to be in a standard form if it is written either in the ascending or descending powers of the variable, as \[1+x+2{{x}^{2}}+3{{x}^{3}}-6{{x}^{5}}\times 6{{x}^{6}}\]
Degree of a polynomial: The highest power of x in p(x) is the degree of the polynomial.

Example: \[2-3{{x}^{5}}+6{{x}^{4}}+92{{x}^{3}}\]: Here, highest term being \[-3{{x}^{5}}\]: degree of polynomial = 5.

Polynomial	General Form	Coefficients
Zero polynomial	\[0\]	\[-\]
Linear polynomial	\[ax+b\]	\[a,b\in R,a\ne 0\]
Quadratic polynomial	\[a{{x}^{2}}+bx+c\]	\[a,b,c\in R,a\ne 0\]
Cubic polynomial	\[a{{x}^{3}}+b{{x}^{2}}+cx+d\]	\[a,b,c,d\in R,a\ne 0\]
Bi-Quadratic polynomial	\[a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+c\]	\[a,b,c,d,e\in R,a\ne 0\]

Value of a polynomial: If p(x) is a polynomial in x, and if ‘a’ is any real number, then the value obtained upon replacing ‘x’ by ‘a’ in p(x) is denoted as p(a).
Zero of a polynomial: A real number ‘a’ for which the value of the polynomial p(x) is zero, is called the zero of the polynomial.
In other words, a real number ‘a’ is called a zero of a polynomial p(x) if p(a) = 0.

Geometric meaning of the zero of a polynomial:
The graph of a linear equation of the form \[y=ax+b,a\ne 0\] is a straight line which intersects the X-axis at\[\left( \frac{-b}{a},0 \right)\]

Zero of the polynomial \[ax+b\]is the x-coordinate of the point of intersection of the graph with X-axis.

Note: A linear polynomial \[ax+b,a\ne 0\]has exactly one zero, i.e., \[\left( \frac{-b}{a} \right)\]

(b) The graph of a quadratic equation \[y=a{{x}^{2}}+bx+c,a\ne 0\]is a curve called parabola that either opens upwards like when the coefficient of\[{{x}^{2}}\] is positive or opens downwards like when the coefficient of\[{{x}^{2}}\] is negative.

The zeros of a quadratic polynomial \[a{{x}^{2}}+bx+c\]are the x-coordinates of the points where the parabola intersects the X-axis.

Example: \[p(x)={{x}^{2}}+2x+4=0;\] \[{{b}^{2}}-4ac\text{ }={{2}^{2}}-4.1.4=-12<0\]

It has no zeros as the parabola will never intersect X-axis.

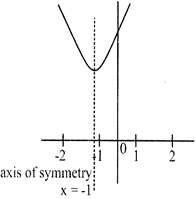
Note: For the parabola \[a{{x}^{2}}+bx+c.\]

(i) Vertex \[\left( \frac{\mathbf{-b}}{\mathbf{2a,}}\mathbf{-}\frac{\mathbf{D}}{\mathbf{4a}} \right)\]where \[\mathbf{D=}{{\mathbf{b}}^{\mathbf{2}}}\mathbf{-4ac}\]

(ii) Axis of symmetry, \[\mathbf{x=}\frac{\mathbf{-b}}{\mathbf{2a}}\] parallel to Y-axis.

(ii) Zeros are\[\frac{\mathbf{-b+}\sqrt{{{\mathbf{b}}^{\mathbf{2}}}\mathbf{-4ac}}}{\mathbf{2a}}\]and \[\frac{\mathbf{-b-}\sqrt{{{\mathbf{b}}^{\mathbf{2}}}\mathbf{-4ac}}}{\mathbf{2a}}\].

(c) The graph of a cubic polynomial intersects the X-axis at three points, whose x-coordinates are the zeros of the cubic polynomial.

In general, the graph of a polynomial of degree ‘n’ y = p(x) passes through at most ‘n’ points on the X-axis. Thus, a polynomial p(x) of degree ‘n’ has at most ‘n’ zeros.

Relationship between zeros and coefficients of a polynomial.

Types of Polynomial	General Form	Number of Zeroes	Relationship between zeroes and coefficients
			Sum of zeroes	Product of zeroes
Linear Polynomial	\[ax+b,\] \[a\ne 0\]	1	\[only\,\,one\,\,zero=\frac{-(constant\,\,term)}{(coefficient\,\,of\,\,x)}=\frac{-b}{a}\]
Quadratic Polynomial	\[a{{x}^{2}}+bx+c,a\ne 0\]	2	\[\frac{-(coefficient\,\,of\,\,x)}{(coefficient\,\,of\,\,{{x}^{2}})}=\frac{-b}{a}\]	\[\frac{constant\,\,term}{coefficient\,\,of\,\,{{x}^{2}}}=\frac{c}{a}\]
Cubic Polynomial	\[a{{x}^{3}}+b{{x}^{2}}+cx,+d,a\ne 0\]	3	\[\frac{-(coefficient\,\,of\,\,x)}{(coefficient\,\,of\,\,{{x}^{2}})}=\frac{-b}{a}\]	\[\frac{cons\tan t\,\,term}{coefficient\,\,of\,\,{{x}^{2}}}=\frac{-d}{a}\]
			Sum of the product of roots taken two at a time \[\frac{coefficient\,of\,x}{coefficient\,of\,{{x}^{2}}}=\frac{c}{a}\].

To form a quadratic polynomial with the given zeros: If \[\alpha \] and \[\beta \] are the zeros of a quadratic polynomial, then the quadratic polynomial is obtained by expanding (\[x-\alpha \]) (\[x-\beta \]). i.e., \[(x-\alpha )(x-\beta )={{x}^{2}}-\](Sum of the zeros) x + product of zeros.
To form a cubic polynomial with the given zeros: If \[\alpha ,\beta \] and \[\gamma \] are the zeros of a polynomial, then the cubic polynomial is obtained by expanding \[(x-\alpha )(x-\beta )(x-\gamma )\].
Division algorithm of polynomials: If \[p\left( x \right)\]and \[g\left( x \right)\]are any two polynomials with\[g(x)\ne 0\], then we can find polynomials \[q\left( x \right)\]and \[r\left( x \right)\]such that\[p\left( x \right)=\text{ }g\left( x \right)\times q\left( x \right)+r\left( x \right)\], where either \[r(x)=0\] or degree \[r\left( x \right)<\]degree of\[g\left( x \right)\].
If \[\left( x-a \right)\] is a factor of polynomial \[p\left( x \right)\]of degree\[n>0\], then ‘a’ is the zero of the polynomial.

Graphical Representation of Different forms of Quadratic Equation

Characteristics of the function	\[{{\mathbf{b}}^{\mathbf{2}}}\mathbf{-4ac<0}\]	\[{{\mathbf{b}}^{\mathbf{2}}}\mathbf{-4ac=0}\]	\[{{\mathbf{b}}^{\mathbf{2}}}\mathbf{-4ac>0}\]
When 'a' is positive i.e. a > 0
When 'a' is negative i.e. a < 0

10th Class Mathematics Polynomials Polynomial

Other Topics

Notes - Polynomial